数据结构和算法(Golang实现)(9)基础知识-算法复杂度及渐进符号

算法复杂度及渐进符号

一、算法复杂度

首先每个程序运行过程中，都要占用一定的计算机资源，比如内存，磁盘等，这些是空间，计算过程中需要判断，循环执行某些逻辑，周而反复，这些是时间。

那么一个算法有多好，多快，怎么衡量一个算法的好坏？所以，计算机科学在算法分析过程中，提出了算法复杂度理论，这套理论可以量化算法的效率，以此作为标准，方便我们能衡量到底选择哪一种算法。

复杂度有两个维度：时间和空间。

我们说，一个实现了某算法的程序：

1. 如果计算的速度越快，那么这个算法时间复杂度越低。
2. 如果占用的计算资源越少，那么空间复杂度越低。

我们要选择复杂度低的算法，衡量好空间和时间的消耗，选出适合特定场景的算法。

这两个复杂度维度的量化过程都是一样的，所以我们这里主要介绍时间复杂度。

二、算法规模

我们要计算公式1 + 2 + 3 + ... + 100，那么按照最直观的算法来写：

package main

import "fmt"

func sum(n int) int {
    total := 0
    // 从1加到N, 1+2+3+4+5+..+N
    for i := 1; i <= n; i++ {
        total = total + i
    }
    return total
}

func main() {
    fmt.Println(sum(100))
}

当n = 10时就等于我们要计算的公式。这个算法要循环n-1次，当n很小时，计算很快，但当n无限大的时候，计算很慢。

所以，算法衡量要衡量的是在不同问题规模 n下，算法的速度。

在这里，因为要循环计算n-1次，而当n无限大时，常数项基本忽略不计，所以这个算法的时间复杂度，我们用O(n)来表示。

我们有另外一种计算方式：

func sum2(n int) int {
    total := ((1 + n) * n) / 2
    return total
}

这次算法只需执行1次，所以这个算法的时间复杂度是O(1)。可以看出，时间复杂度为O(1)的算法优于复杂度为O(n)的算法。

当然，还有指数级别的比如之前的汉诺塔算法，对数级别的，阶乘级别的复杂度，如O(2^n)，O(n!)，O(logn)等。

算法的优先级排列如下，一般排在上面的要优于排在下面的：

1. 常数复杂度：O(1)
2. 对数复杂度：O(logn)
3. 一次方复杂度：O(n)
4. 一次方乘对数复杂度：O(nlogn)
5. 乘方复杂度：O(n^2)，O(n^3)
6. 指数复杂度：O(2^n)
7. 阶乘复杂度：O(n!)
8. 无限大指数复杂度：O(n^n)

三、渐进符号

如何量化一个复杂度，到底有多复杂，计算机科学抽象出了几个复杂度渐进符号。

渐进符号如下：

O，ο，Θ，Ω，ω

分别读作：Omicron（大欧），omicron（小欧），Theta（西塔），Omega（大欧米伽），omega（小欧米伽）。

3.1. 渐进符号：Θ

假设算法A的运行时间表达式：

T(n)= 5 * n^3 + 4 * n^2

如果问题规模n足够大，那么低次方的项将无足轻重，运行时间主要取决于高次方的第一项：5*n^3。

随着n的增大，第一项的5*n^3中的常数5也无足轻重了。

所以算法A的运行时间T(n)约等于n^3。记为：

T(n) = Θ(n^3)

Θ的数学含义:

设f(n)和g(n)是定义域n为自然数集合的函数，两个函数同阶，也就是当n无穷大时，f(n)/g(n)等于某个大于0的常数c。

也可以说，存在正常量c1，c2和n0，对于所有n >= n0，有0 <= c1 * g(n) <= f(n) <= c2 * g(n)。

那么可以记f(n) = Θ(g(n))，g(n)是f(n)的渐进紧确界。

3.2. 渐进符号：O

O的数学含义:

设f(n)和g(n)是定义域n为自然数集合的函数，f(n)函数的阶不高于g(n)函数的阶。

也可以说，存在正常量c和n0，对于所有n >= n0，有0 <= f(n) <= c * g(n)。

那么可以记f(n) = O(g(n))。g(n)是f(n)的渐进上界。

3.3. 渐进符号：Ω

Ω的数学含义:

设f(n)和g(n)是定义域n为自然数集合的函数，f(n)函数的阶不低于g(n)函数的阶。

也可以说，存在正常量c和n0，对于所有n >= n0，有0 <= cg(n) <= f(n)。

那么可以记f(n) = Ω(g(n))。g(n)是f(n)的渐进下界。

3.4. 渐进分析

上面的定义很复杂，我们可以来看图：

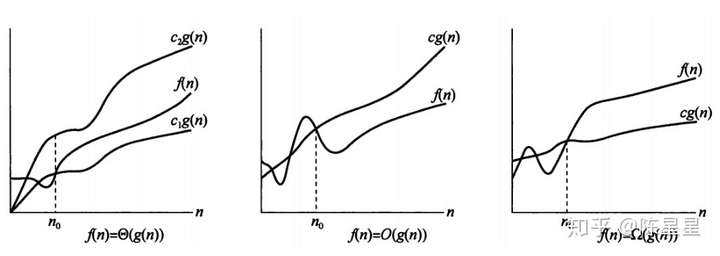
当n值超过某个值时，f(n)被g(n)两条线夹在中间，那么g(n)就是渐进紧确界。

如果g(n)的线在上面，就是渐进上界。

如果g(n)线在下面，就是渐进下界。

我们一般会评估一个算法的渐进上界O，因为这表示算法的最坏情况，这个上界可以十分不准确，但我们一般会评估得足够准确，比如：

设 f(n) = 5 * n^3 + 4 * n^2，我们要求渐进上界。

那么：

f(n) = O(n^3)，g(n) = n^3
f(n) = O(n^4)，g(n) = n^4

两个g(n)都是上界，因为令c = 5时都存在：0 <= f(n) <= c * g(n))。

我们会取乘方更小的那个，因为这个界更逼近f(n)本身，所以我们一般说f(n) = O(n^3)，算法的复杂度为大欧n的三次方，表示最坏情况。

同理，渐进下界Ω刚好与渐进上界相反，表示最好情况。比如还是这个假设：

设 f(n) = 5 * n^3 + 4 * n^2，我们要求渐进下界。

那么：

f(n) = Ω(n^3)，g(n) = n^3
f(n) = Ω(n^2)，g(n) = n^2

两个g(n)都是下界，因为令c =5时都存在：0 <= cg(n) <= f(n)。

我们准确评估的时候，要取乘方更大的那个，因为这个界更逼近f(n)本身，所以我们一般说f(n) = Ω(n^3)，算法的复杂度为大欧米伽n的三次方，表示最好情况。

我们发现当f(n) = Ω(n^3) = O(n^3)时，其实f(n) = Θ(n)。

另外两个渐进符号ο和ω一般很少使用，指不那么紧密的上下界。

也就是评估的时候，不那么准确去评估，在评估最坏情况的时候使劲地往坏了评估，评估最好情况则使劲往好的评估，但是它不能刚刚好，比如上面的结果：

f(n) = O(n^3)，g(n) = n^3
f(n) = O(n^4)，g(n) = n^4
f(n) = Ω(n^3)，g(n) = n^3
f(n) = Ω(n^2)，g(n) = n^2

我们可以说：

f(n) = ο(n^4)，g(n) = n^4  往高阶的评估，不能同阶
f(n) = ω(n^2)，g(n) = n^2  往低阶的评估，不能同阶

四、总结

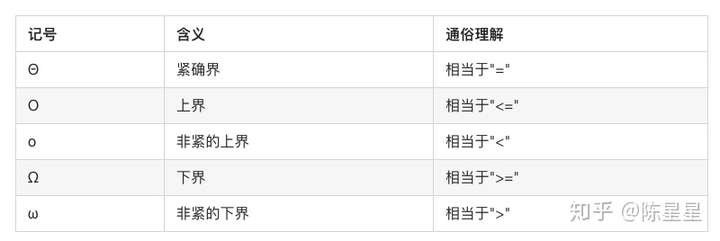
我们一般用O渐进上界来评估一个算法的时间复杂度，表示逼近的最坏情况。其他渐进符合基本不怎么使用。

系列文章入口

我是陈星星，欢迎阅读我亲自写的 数据结构和算法(Golang实现)，文章首发于 阅读更友好的GitBook。

• 数据结构和算法(Golang实现)(1)简单入门Golang-前言
• 数据结构和算法(Golang实现)(2)简单入门Golang-包、变量和函数
• 数据结构和算法(Golang实现)(3)简单入门Golang-流程控制语句
• 数据结构和算法(Golang实现)(4)简单入门Golang-结构体和方法
• 数据结构和算法(Golang实现)(5)简单入门Golang-接口
• 数据结构和算法(Golang实现)(6)简单入门Golang-并发、协程和信道
• 数据结构和算法(Golang实现)(7)简单入门Golang-标准库
• 数据结构和算法(Golang实现)(8.1)基础知识-前言
• 数据结构和算法(Golang实现)(8.2)基础知识-分治法和递归
• 数据结构和算法(Golang实现)(9)基础知识-算法复杂度及渐进符号
• 数据结构和算法(Golang实现)(10)基础知识-算法复杂度主方法
• 数据结构和算法(Golang实现)(11)常见数据结构-前言
• 数据结构和算法(Golang实现)(12)常见数据结构-链表
• 数据结构和算法(Golang实现)(13)常见数据结构-可变长数组
• 数据结构和算法(Golang实现)(14)常见数据结构-栈和队列
• 数据结构和算法(Golang实现)(15)常见数据结构-列表
• 数据结构和算法(Golang实现)(16)常见数据结构-字典
• 数据结构和算法(Golang实现)(17)常见数据结构-树
• 数据结构和算法(Golang实现)(18)排序算法-前言
• 数据结构和算法(Golang实现)(19)排序算法-冒泡排序
• 数据结构和算法(Golang实现)(20)排序算法-选择排序
• 数据结构和算法(Golang实现)(21)排序算法-插入排序
• 数据结构和算法(Golang实现)(22)排序算法-希尔排序
• 数据结构和算法(Golang实现)(23)排序算法-归并排序
• 数据结构和算法(Golang实现)(24)排序算法-优先队列及堆排序
• 数据结构和算法(Golang实现)(25)排序算法-快速排序
• 数据结构和算法(Golang实现)(26)查找算法-哈希表
• 数据结构和算法(Golang实现)(27)查找算法-二叉查找树
• 数据结构和算法(Golang实现)(28)查找算法-AVL树
• 数据结构和算法(Golang实现)(29)查找算法-2-3树和左倾红黑树
• 数据结构和算法(Golang实现)(30)查找算法-2-3-4树和普通红黑树