FOC 算法基础之欧拉公式

文章目录

欧拉公式
几何意义

复数平面
动态过程
加法

FOC电压矢量的推导
总结
参考

FOC中电压矢量合成的推导，对于欧拉公式的几何意义做了一个全面的回顾。

欧拉公式

欧拉是一个天才，欧拉公式甚至被誉为上帝创造的公式，然后在FOC算法中也可以看到欧拉公式的影子，不过因为是最基础的知识，所以基本上的换算都是一笔带过，但是如果这里没有掌握就很难搞清楚实数平面如何换算到复数平面，以至于在SVPWM的求解中存在的都是向量运算，所以这里有必要理解欧拉公式的物理意义，这样可以加深FOC算法的理解。

欧拉公式如下所示；

{eix=cosx+isinx⋯①eπi+1=0⋯②\begin{cases}
e^{ix} = cosx + isinx \cdots ①\\
e^{\pi i} + 1 = 0 \cdots ②
\end{cases}
{eix=cosx+isinx⋯①eπi+1=0⋯②

这两个公式都被称之为欧拉公式；

eee 是自然对数的底，iii 是虚数（i=−1i=\sqrt{-1}i=−1）。

根据式 ① 可以推导出以下另外两个变式；

推导过程如下；

令x=−xx = -xx=−x，可以得到④式，如下；

{eix=cosx+isinx⋯③e−ix=cosx−isinx⋯④\begin{cases}
e^{ix} = cosx + isinx \cdots ③\\
e^{-ix} = cosx - isinx \cdots ④\\
\end{cases}
{eix=cosx+isinx⋯③e−ix=cosx−isinx⋯④

所以 ③ 等式左右两端与 ④ 式相加得到；

cosx=eix+e−ix2⋯⑤
cosx = \cfrac{e^{ix}+e^{-ix}}{2}\cdots ⑤
cosx=2eix+e−ix⋯⑤

所以 ③ 等式左右两端与 ④ 式相减得到；

sinx=eix−e−ix2i⋯⑥
sinx = \cfrac{e^{ix}-e^{-ix}}{2i}\cdots ⑥
sinx=2ieix−e−ix⋯⑥

几何意义

reiθre^{i\theta}reiθ则表示模长为rrr的向量旋转了角度θ\thetaθ，下面会进一步介绍。

复数平面

复数平面坐标xxx轴作为实数轴，yyy轴作为虚数轴。这里可以通过欧拉公式，将实数平面换到复数平面，如下图所示；

已知这是一个半径为rrr，圆心为OOO的圆，则存在；

reiθ=r(cosθ+isinθ)
re^{i\theta} = r(cos\theta + isin\theta)
reiθ=r(cosθ+isinθ)

上式表示向量 OP→\overrightarrow{OP}OP 逆时针旋转了角度 θ\thetaθ , ∣OP→∣=r| \overrightarrow{OP}| = r∣OP∣=r；

动态过程

假设向量OC→\overrightarrow{OC}OC逆时针旋转，与xxx轴夹角为θ\thetaθ，半径r=10r = 10r=10，即 ∣OC→∣=r=10| \overrightarrow{OC}| = r =10∣OC∣=r=10，具体如下图所示；

这里分析一下图中的几个关键点；

红色点的坐标为：(θ,10sinθ)(\theta, 10sin\theta)(θ,10sinθ)，红色的正弦曲线为红色点的运动轨迹；
绿色点的坐标为；(10cosθ,θ)(10cos\theta, \theta)(10cosθ,θ)，绿色的正弦曲线为绿色点的运动轨迹；
CGCGCG为向量OC→\overrightarrow{OC}OC在xxx轴上的投影，∣CG∣=10cosθ|CG| = 10cos\theta∣CG∣=10cosθ；
CHCHCH为向量OC→\overrightarrow{OC}OC在yyy轴上的投影，∣CH∣=10sinθ|CH| = 10sin\theta∣CH∣=10sinθ；

可以发现，向量在复平面做圆周运动，其实数域相当于是在做正弦运动。后面再FOC中的三相正弦波形的合成可以做一下分析。

加法

欧拉公式里的相加则比较简单，相当于两个向量的相加；

AE→=AC→+AD→\overrightarrow{AE} = \overrightarrow{AC} + \overrightarrow{AD}AE=AC+AD

如下图所示；

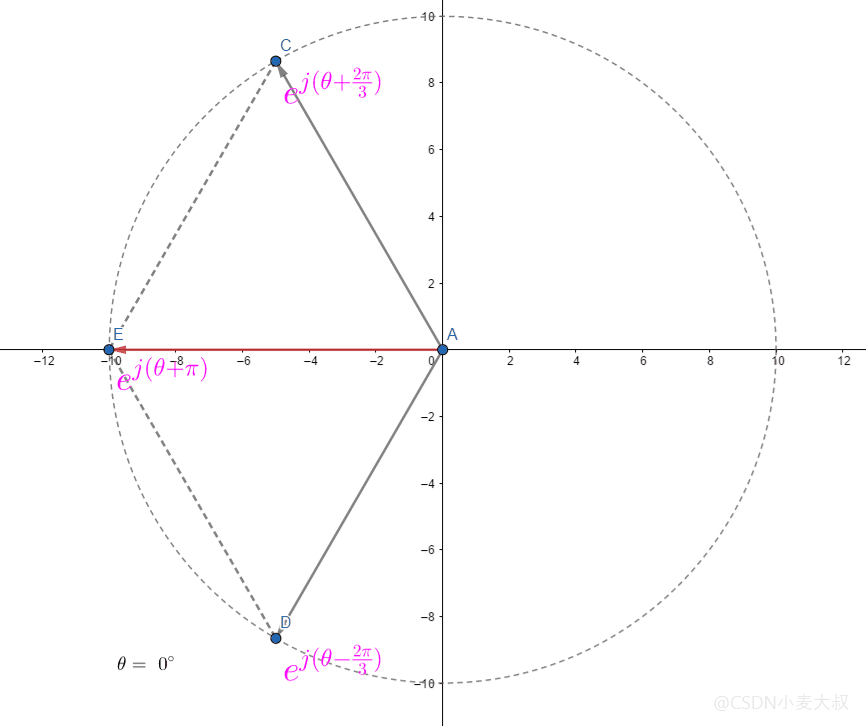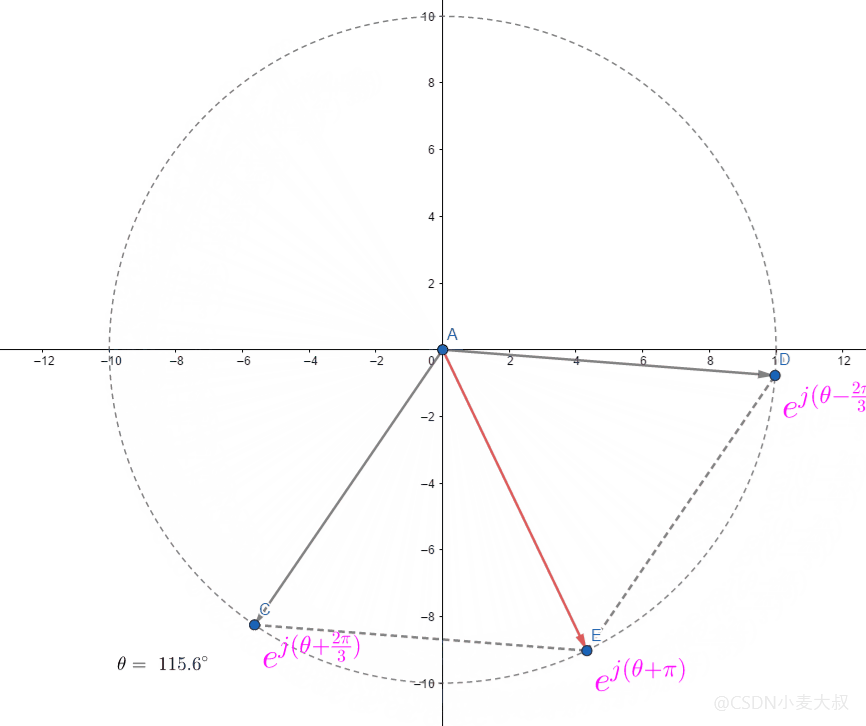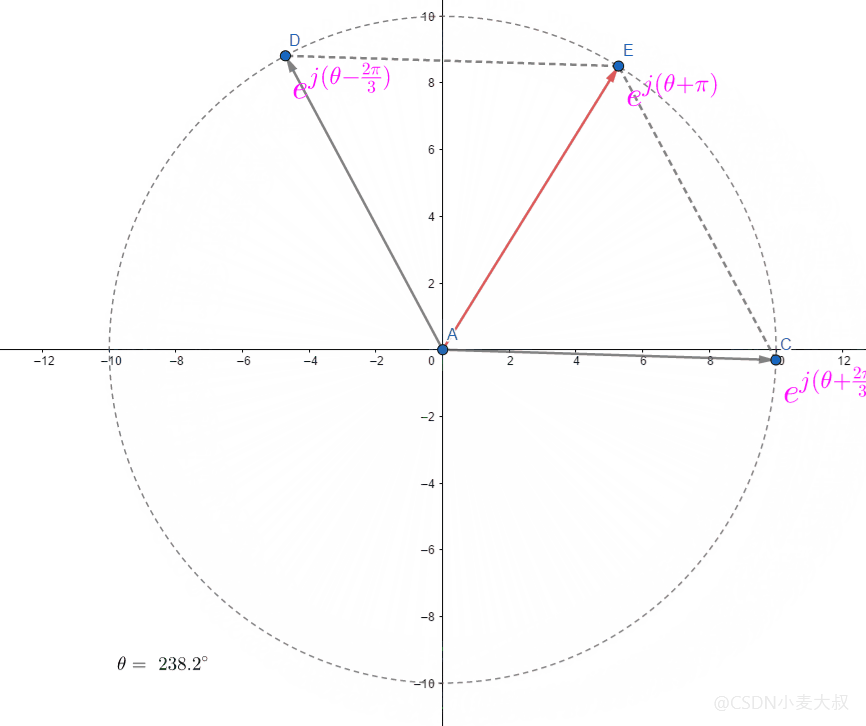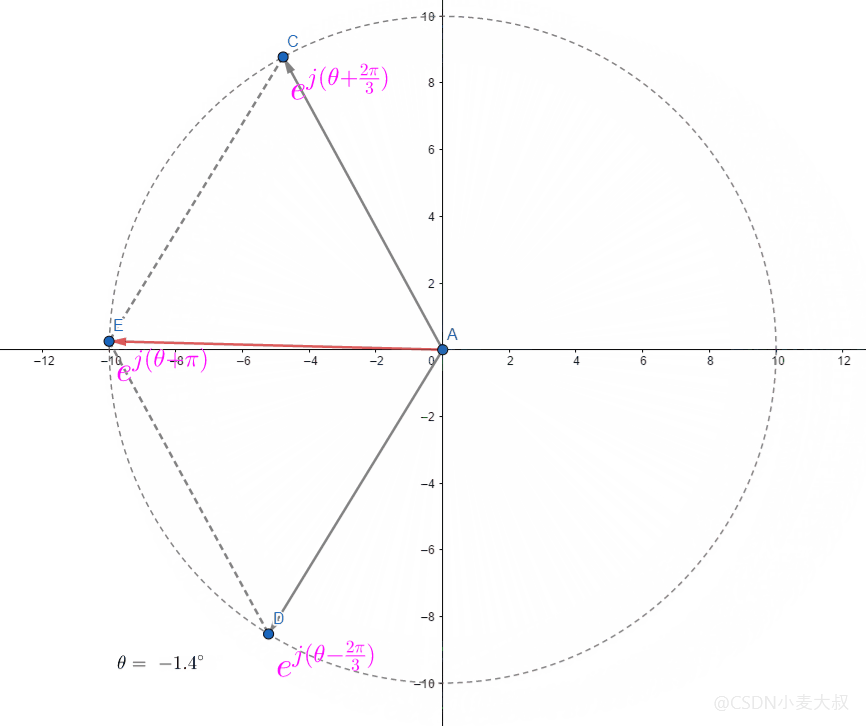
所以存在特殊情况当 θ=0\theta = 0θ=0时则有；

AE→=∣AE→∣(ej(θ+2π3)+ej(θ−2π3))\overrightarrow{AE} = |\overrightarrow{AE}|(e^{j(\theta+\cfrac{2\pi}{3})} + e^{j(\theta-\cfrac{2\pi}{3})} )AE=∣AE∣(ej(θ+32π)+ej(θ−32π))

直接进行符合向量相加；

AE→=∣AE→∣ej(θ+π)\overrightarrow{AE} = |\overrightarrow{AE}|e^{j(\theta+\pi)}AE=∣AE∣ej(θ+π)

具体如下所示；

FOC电压矢量的推导

三相永磁同步电机的驱动电路如下图所示；

详细的坐标变换可以参考《FOC中的Clarke变换和Park变换详解》，根据图示电路可以发现在三相永磁同步电机的驱动电路中，三相逆变输出的三相电压为UAU_{A}UA，UBU_{B}UB，UCU_{C}UC将作用于电机，那么在三相平面静止坐标系ABC中，电压方程满足以下公式：

{UA=UmcosθeUB=Umcos(θe−2π3)UC=Umcos(θe+2π3) \begin{cases}
U_{A} = U_{m}cos\theta_{e} \\
U_{B} = U_{m}cos(\theta_{e} - \cfrac{2\pi}{3}) \\
U_{C} = U_{m}cos(\theta_{e} + \cfrac{2\pi}{3})
\end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧UA=UmcosθeUB=Umcos(θe−32π)UC=Umcos(θe+32π)

UmU_mUm为相电压基波峰值；

因此根据前面式⑤cosx=eix+e−ix2⋯⑤
cosx = \cfrac{e^{ix}+e^{-ix}}{2}\cdots ⑤
cosx=2eix+e−ix⋯⑤

可以将该方程组转换到复平面可以得到，下式统一使用θ\thetaθ 表示θe\theta_{e}θe；

{UA=Umcosθe=Um2(eiθ+e−iθ)UB=Umcos(θe+2π3)=Um2(e(iθ−2π3)+e−(iθ−2π3))UC=Umcos(θe−2π3)=Um2(e(iθ+2π3)+e−(iθ+2π3)) \begin{cases}
U_{A}= U_{m}cos\theta_{e} = \cfrac{ U_{m}}{2}(e^{i\theta} + e^{-i\theta})\\
U_{B}= U_{m}cos(\theta_{e} + \cfrac{2\pi}{3}) = \cfrac{ U_{m}}{2}(e^{(i\theta-\cfrac{2\pi}{3})} + e^{-(i\theta-\cfrac{2\pi}{3})})\\
U_{C} = U_{m}cos(\theta_{e} - \cfrac{2\pi}{3}) = \cfrac{ U_{m}}{2}(e^{(i\theta+\cfrac{2\pi}{3})} + e^{-(i\theta+\cfrac{2\pi}{3})})
\end{cases}⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧UA=Umcosθe=2Um(eiθ+e−iθ)UB=Umcos(θe+32π)=2Um(e(iθ−32π)+e−(iθ−32π))UC=Umcos(θe−32π)=2Um(e(iθ+32π)+e−(iθ+32π))

因为需要将三相电压合成矢量 U→=UA→+UB→+UC→\overrightarrow{U} = \overrightarrow{U_A} + \overrightarrow{U_B} + \overrightarrow{U_C}U=UA+UB+UC；下面增加向量的相位差；

{UA→=UA∗ej0UB→=UB∗e−(j2π3)UC→=UC∗e(j2π3) \begin{cases}
\overrightarrow{U_A} = U_A *e^{j0}\\
\overrightarrow{U_B} = U_B *e^{-(j\cfrac{2\pi}{3})} \\
\overrightarrow{U_C} = U_C *e^{(j\cfrac{2\pi}{3})}\\
\end{cases}⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧UA=UA∗ej0UB=UB∗e−(j32π)UC=UC∗e(j32π)

中间推导过程暂略，最终推导得到；

U→=32Umejθ=32Umejωt\overrightarrow{U} = \cfrac{3}{2}U_me^{j\theta} = \cfrac{3}{2}U_me^{j\omega t} U=23Umejθ=23Umejωt

总结

磕磕绊绊写了最后，基础学科的掌握还不够，很多知识回过头来看，总会有新的收获，但是由于笔者能力有限，文中难免出行错误和纰漏，望您能不吝赐教。

参考

https://www.matongxue.com/madocs/8.html