第八次-非确定的自动机NFA确定化为DFA
NFA 确定化为 DFA
子集法:
f(q,a)={q1,q2,…,qn},状态集的子集
将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合。
步骤:
1.根据NFA构造DFA状态转换矩阵
①确定DFA初态(NFA的所有初态集),字母表
②从初态出发,经字母表到达的状态集看成一个新状态
③将新状态添加到DFA状态集
④重复23步骤,直到没有新的DFA状态
2.画出DFA
3.看NFA和DFA识别的符号串是否一致。
练习:
1.解决多值映射:子集法
1). 发给大家的图1
2). P64页练习3
2.解决空弧:对初态和所有新状态求ε-闭包
1). 发给大家的图2
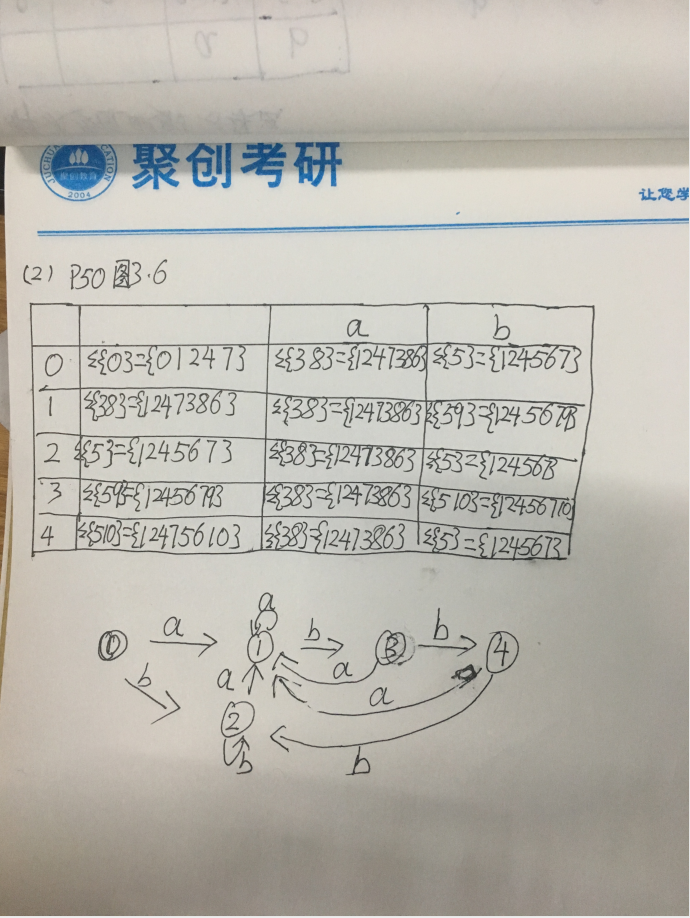
2).P50图3.6
解:
第八次-非确定的自动机NFA确定化为DFA的更多相关文章
- 第八次——非确定的自动机NFA确定化为DFA
NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. 步骤: 1. ...
- 第八次作业-非确定的自动机NFA确定化为DFA
NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. 步骤: 1. ...
- 作业八——非确定的自动机NFA确定化为DFA
NFA 确定化为 DFA 子集法: f(q,a)={q1,q2,…,qn},状态集的子集 将{q1,q2,…,qn}看做一个状态A,去记录NFA读入输入符号之后可能达到的所有状态的集合. 步骤: 1. ...
- 非确定的自动机NFA确定化为DFA
摘要: 在编译系统中,词法分析阶段是整个编译系统的基础.对于单词的识别,有限自动机FA是一种十分有效的工具.有限自动机由其映射f是否为单值而分为确定的有限自动机DFA和非确定的有限自动机NFA.在非确 ...
- 编译原理之非确定的自动机NFA确定化为DFA
1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} ),其中 f(0,a)={0,1} f(0,b)={0} f(1,b)={2} f(2,b)={3} 画出状态转换矩阵 ...
- 编译原理:非确定的自动机NFA确定化为DFA
1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} ),其中 f(0,a)={0,1} f(0,b)={0} f(1,b)={2} f(2,b)={3} 画出状态转换矩阵 ...
- NFA转化为DFA
NFA(不确定的有穷自动机)转化为DFA(确定的有穷自动机) NFA转换DFA,通常是将带空串的NFA(即:ε-NFA)先转化为不带空串的NFA(即:NFA),然后再转化为DFA. 提示:ε是空串的意 ...
- 非确定有限状态自动机的构建(二)——将CharVal转换为NFA
保留版权,转载注明出处:潘军彪的个人博客(http://blog.csdn.net/panjunbiao/article/details/9378933) 将上下文无关文法读入内存之后,可以将它转换成 ...
- 非确定有限状态自动机的构建(一)——NFA的定义和实现
保留版权,转载需注明出处(http://blog.csdn.net/panjunbiao). 非确定有限状态自动机(Nondeterministic Finite Automata,NFA)由以下元素 ...
随机推荐
- 一些常用关键字的用法(一.static)
17:36:26 2020-04-05 又是充实的一天,刚刚开始学习不久java的我,从面向过程的语言转变到面向对象的语言,在思想上上还是需要花费很多时间转变的.今天学习到了这几个关键字了,觉得这几个 ...
- [POJ1190]生日蛋糕<DFS>
题目链接:http://poj.org/problem?id=1190 题看上去确实很复杂 涉及到半径面积这些,其实看着真的很头疼 但是除去这些就是剪枝优化的dfs算法 #include<cst ...
- PTA | 1008 数组元素循环右移问题 (20分)
一个数组A中存有N(N>0)个整数,在不允许使用另外数组的前提下,将每个整数循环向右移M(M>=0)个位置,即将A中的数据由(A0 A1--AN-1)变换为(AN-M -- AN-1 A0 ...
- CF633(div.2)A. Filling Diamonds
题目描述 http://codeforces.com/contest/1339/problem/A 给定一个 \(n(1\le n \le 10^9)\) ,问用一个由两个三角形组成的菱形,填充下面这 ...
- Docker的简介以及Dockerfile编写与使用
Docker的简介 Docker是在容器的基础上,进行了进一步的封装,极大的简化了容器的创建和维护.使得Docker技术比虚拟机技术更为轻便.快捷. 下面是两张对比图. 可以看到传统虚拟机技术是虚拟出 ...
- stdio.h file not found mac catalina clion 头文件 找不到
问题:mac update catalina 版本之后引发的include文件问题 近期Mac 版本升级到catalina版本,使用CLion调试c/c++程序,莫名其妙的发现,有些头文件incl ...
- 10-jmeter 测试soap协议v1.2版本请求
1.因为jmeter安装了第三方插件jmeter-plugins-manager.jar之后(具体安装看之前文章),此时就可简单直接测试soap协议1.2版本的请求了 2. 3.进行运行线程就可实现了 ...
- Jmeter常用元件
1.测试计划:测试元件的容器,相当于一个项目名称 线程组: 2.监听器:负责收集测试结果,同时也被告知了结果显示的方式 (1)查看结果树:看具体某个请求——请求响应,结果明细 (2)聚合报告:汇总报 ...
- Flutter 吐血整理组件继承关系图
老孟导读:前几天一个读者和我说能不能整理一个各个控件之间的继承关系,这2天抽时间整理了一下,不整理不知道,一整理真的吓一跳啊,仅仅Widget的子类(包括间接子类)就高达353个,今天发群里给大家浏览 ...
- 谁说.NET不适合搞大数据,机器学习、人工智能
SciSharp Stack SciSharp STACK: https://scisharp.github.io/SciSharp/ 基于.NET的开源生态系统,用于数据科学.机器学习和AI. Sc ...
