【数学/扩展欧几里得/线性求逆元】[Sdoi2008]沙拉公主的困惑

---

Description

　　大富翁国因为通货膨胀，以及假钞泛滥，政府决定推出一项新的政策：现有钞票编号范围为1到N的阶乘，但是，政府只发行编号与M!互质的钞票。房地产第一大户沙拉公主决定预测一下大富翁国现在所有真钞票的数量。现在，请你帮助沙拉公主解决这个问题，由于可能张数非常大，你只需计算出对R取模后的答案即可。R是一个质数。

Input

　　第一行为两个整数T，R。R<=10^9+10，T<=10000，表示该组中测试数据数目，R为模后面T行，每行一对整数N，M，见题目描述 m<=n

Output

　　共T行，对于每一对N，M，输出1至N！中与M！素质的数的数量对R取模后的值

---

　　首先以为n>=m,所以m!是n!的因数,所以每次找到一个与m!互质的数，那么我们就可以得到n!/m!个数与m!互质。

　　所以答案就是phi(m!)*n!/m!。

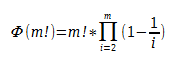　　(i为质数)

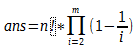　　那么易得(i为质数)

　　然后线性求1-1000W的fac[i](i!%R)和inv[i](i的逆元)即可(素数用exgcd，其他的用到inv是个积性函数(i,j互质，f[i*j]=f[i]*f[j]))。

　　phi值可以不用线性筛。。O(sqrt(n))求单个即可，实际效率更高。

　　inv只需要求素数的就可以辣。。（求其他的亲测tle,可能超时。。）

　　还有一个ans数组记录n!后面那一坨的值，具体求法:是素数，那么就ans[i]=ans[i]*(i-1)*inv[i]。(记得mod)，否则不动，不过不管是不是素数，在操作之前都要ans[i]=ans[i-1]，三个数组的头号元素值都是1.

　　

 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>

 #define maxn 10000000

 typedef long long ll;

 using namespace std;

 int prime[maxn+],b=,inv[maxn+],mod,fac[maxn+],x,y,ans[maxn+];

 bool is_prime[maxn+];

 void exgcd(int n,int m)
 {
     if(m==){x=,y=;return;}
     exgcd(m,n%m);
     ll t=x;
     x=y,y=t-n/m*y;
 }

 void work()
 {
     inv[]=,fac[]=;
     for(int i=;i<=maxn&&i<mod;i++)fac[i]=(ll)i*fac[i-]%mod;
     for(int i=;i<=maxn;i++)
     {
         if(!is_prime[i])prime[++b]=i,exgcd(i,mod),inv[i]=(x%mod+mod)%mod;
         int j=,t=*i;
         while(j<=b&&t<=maxn)
         {
             is_prime[t]=;
             if(i%prime[j]==)break;
         //    inv[t]=inv[i]*inv[prime[j]]%mod;
             t=prime[++j]*i;
         }
     }
     ans[]=;
     for(int i=;i<=maxn;i++)
     {
         ans[i]=ans[i-];
         if(!is_prime[i])ans[i]=(ll)ans[i]*(i-)%mod*inv[i]%mod;
     }
 }

 int main()
 {
     int T;
     scanf("%d%d",&T,&mod);
     work();
     while(T--)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         printf("%d\n",(ll)fac[x]*ans[y]%mod);
     }
     return ;
 }

　　 long long什么的卡的我不要不要的。。