redis发布订阅、HyperLogLog与GEO功能的介绍
一、发布订阅
1、模型
发布者发布消息,订阅者接收消息
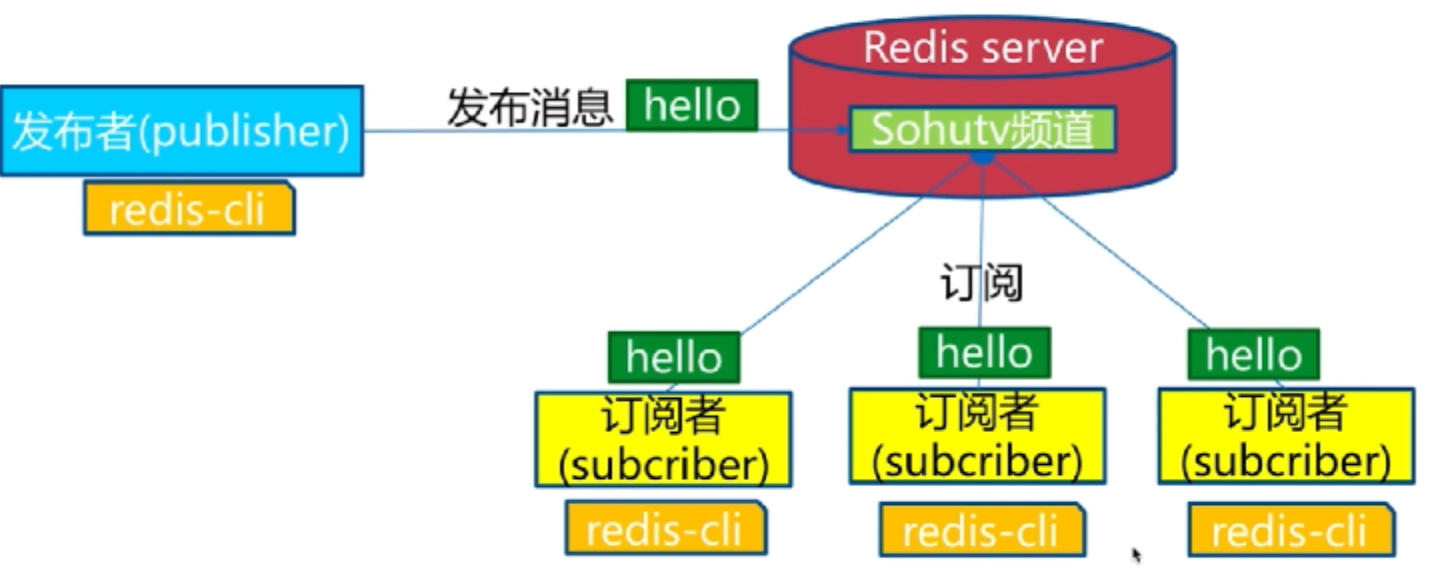
2、API
2.1、publish

2.2、订阅

2.3、取消订阅
unsubsribe

2.4、其他api

二、HyperLogLog
极小空间完成独立数量的统计,本质是字符串类型

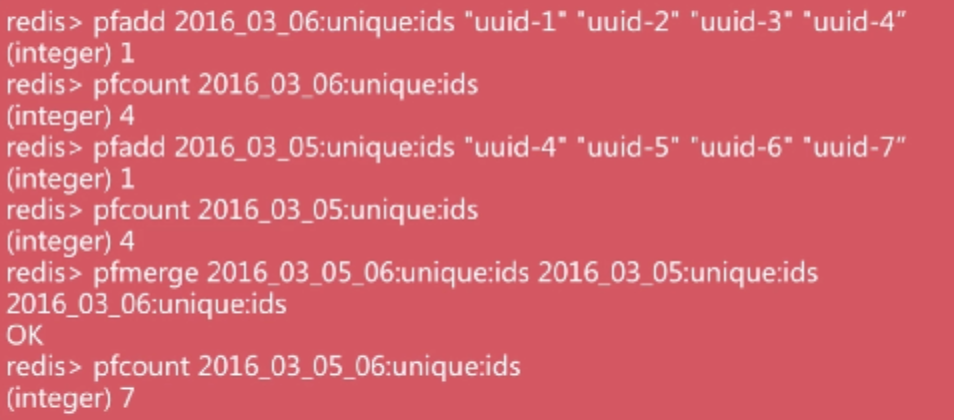
优势:百万数据只占十几k内存
局限:错误率:0.81%,不能取出单条数据
三、GEO
存储经纬度,计算两地距离,范围计算等
使用场景:距离范围内的酒店、餐馆、摇一摇等
1、geoadd 添加坐标

2、geopos 获取地理位置

3、geodist

4、georadius

redis发布订阅、HyperLogLog与GEO功能的介绍的更多相关文章
- redis 发布订阅、geo、bitmap、hyperloglog
1.发布订阅 简介 发布订阅类似于广播功能.redis发布订阅包括 发布者.订阅者.Channel 命令 命令 作用 时间复杂度 subscribe channel 订阅一个频道 O(n) unsub ...
- Redis 发布订阅,小功能大用处,真没那么废材!
今天小黑哥来跟大家介绍一下 Redis 发布/订阅功能. 也许有的小伙伴对这个功能比较陌生,不太清楚这个功能是干什么的,没关系小黑哥先来举个例子. 假设我们有这么一个业务场景,在网站下单支付以后,需要 ...
- python中使用redis发布订阅者模型
redis发布订阅者模型: Redis提供了发布订阅功能,可以用于消息的传输,Redis的发布订阅机制包括三个部分,发布者,订阅者和Channel.发布者和订阅者都是Redis客户端,Channel则 ...
- MariaDB主从复制,redis发布订阅,持久化,以及主从同步
一. MariaDB主从复制 mysql基本操作 1 连接数据库 mysql -u root -p -h 127.0.0.1 mysql -u root -p -h 192.168.12.60 2 ...
- Redis发布订阅机制
1. 什么是Redis Redis是一个开源的内存数据库,它以键值对的形式存储数据.由于数据存储在内存中,因此Redis的速度很快,但是每次重启Redis服务时,其中的数据也会丢失,因此,Redis也 ...
- Linux 安装redis,redis发布订阅,持久化
安装redis 1.安装redis的方式 -yum (删除这个yum安装的redis,我们只用源码编译安装的) -rpm -源码编译 2.删除原本的redis yum remove redis -y ...
- Linux(6)- redis发布订阅/持久化/主从复制/redis-sentinel/redis-cluster、nginx入门
一.redis发布订阅 Redis 通过 PUBLISH .SUBSCRIBE 等命令实现了订阅与发布模式. 其实从Pub/Sub的机制来看,它更像是一个广播系统,多个Subscriber可以订阅多个 ...
- 我在生产项目里是如何使用Redis发布订阅的?(一)使用场景
转载请注明出处! 导语 Redis是我们很常用的一款nosql数据库产品,我们通常会用Redis来配合关系型数据库一起使用,弥补关系型数据库的不足. 其中,Redis的发布订阅功能也是它的一大亮点.虽 ...
- redis 学习(12)-- redis 发布订阅
redis 发布订阅 发布订阅模式中的角色 发布者(publisher) 订阅者(subscriber) 频道(channel) 如图所示: 发布者发布消息到频道,订阅了频道的订阅者可以收到消息,订阅 ...
随机推荐
- 基于Thinkphp5+phpQuery 网络爬虫抓取数据接口,统一输出接口数据api
TP5_Splider 一个基于Thinkphp5+phpQuery 网络爬虫抓取数据接口 统一输出接口数据api.适合正在学习Vue,AngularJs框架学习 开发demo,需要接口并保证接口不跨 ...
- Java中WeakHashMap实现原理深究
一.前言 我发现Java很多开源框架都使用了WeakHashMap,刚开始没怎么去注意,只知道它里面存储的值会随时间的推移慢慢减少(在 WeakHashMap 中,当某个“弱键”不再正常使用时,会被从 ...
- [剑指Offer] 7.斐波那契数列
class Solution { public: int Fibonacci(int n) { ] = {}; res[] = ; res[] = ; ;i < n;i ++){ res[i] ...
- 【bzoj3000】Big Number 数论
题目描述 给你两个整数N和K,要求你输出N!的K进制的位数. 输入 有多组输入数据,每组输入数据各一行,每行两个数——N,K 输出 每行一个数为输出结果. 样例输入 2 5 2 10 10 10 10 ...
- P1368 工艺
题目描述 小敏和小燕是一对好朋友. 他们正在玩一种神奇的游戏,叫Minecraft. 他们现在要做一个由方块构成的长条工艺品.但是方块现在是乱的,而且由于机器的要求,他们只能做到把这个工艺品最左边的方 ...
- [NOI.AC省选模拟赛3.23] 集合 [数学]
题面 传送门 一句话题意: 给定$n\leq 1e9,k\leq 1e7,T\leq 1e9$ 设全集$U=\lbrace 1,2,3,...n\rbrace $,求$(min_{x\in S}\lb ...
- [Leetcode] palindrome partition ii 回文分区
Given a string s, partition s such that every substring of the partition is a palindrome. Return the ...
- Covered Points Count(思维题)
C. Covered Points Count time limit per test 3 seconds memory limit per test 256 megabytes input stan ...
- ACM模板~求第k短路 ~~~A*+Dijkstra
#include <map> #include <set> #include <cmath> #include <ctime> #include < ...
- springboot之mybatis别名的设置
mybatis别名设置 在具体的mapper.xml文件中,定义很多的statement,statement需要parameterType指定输入参数的类型.需要resultType指定输出结果的映射 ...
