洛谷 P3371 【模板】单源最短路径 【链式前向星+SPFA】

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

4 6 1

1 2 2

2 3 2

2 4 1

1 3 5

3 4 3

1 4 4

输出样例#1：

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

样例说明：



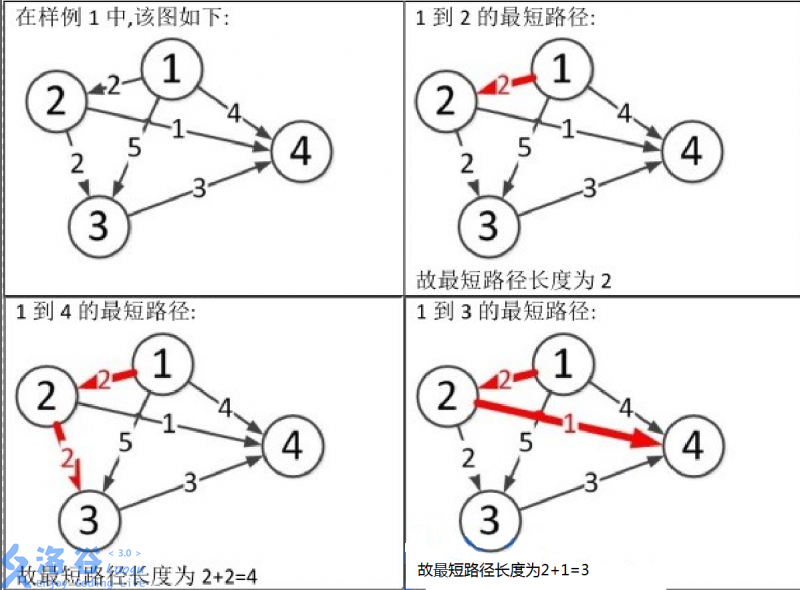
图片1到3和1到4的文字位置调换

#include <stdio.h>
#include <string.h>
#include <string>
#include <iostream>
#include <stack>
#include <queue>
#include <vector>

using namespace std;

const int maxn = 10005;
const int maxm = 500005; //一定要注意数组大小！
const int inf = 2147483647;
int n,m;
int x,y,z,s;
int k=0;
struct node
{
    int to,w,next;
}e[maxm];
int head[maxm],dis[maxn],vis[maxn];
void add(int u,int v,int w)
{
    e[++k].to=v;
    e[k].next=head[u];
    e[k].w=w;
    head[u]=k;
}
queue<int> q;
void spfa(int st)
{
    for(int i=1;i<=n;i++)
    {
        dis[i]=inf;
        vis[i]=0;
    }
    dis[st]=0;
    vis[st]=1;
    q.push(st);
    while(!q.empty())
    {
        int now = q.front();
        q.pop();
        vis[now]=0;
        for(int i=head[now]; i; i=e[i].next)
        {
            int ed = e[i].to;
            if(dis[ed] > dis[now] + e[i].w)
            {
                dis[ed] = dis[now]+e[i].w;
                if(!vis[ed])
                {
                    q.push(ed);
                    vis[ed]=1;
                }
            }
        }
    }
}

int main()
{
    scanf("%d%d%d",&n,&m,&s);
    memset(dis,inf,sizeof(dis));
    memset(vis,0,sizeof(vis));
    memset(head,-1,sizeof(head));
    k=0;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z); //有向图
    }
    spfa(s);
    for(int i=1;i<=n;i++)
        printf("%d ",dis[i]);
}
/*
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
*/