GDSOI2015的某道题目

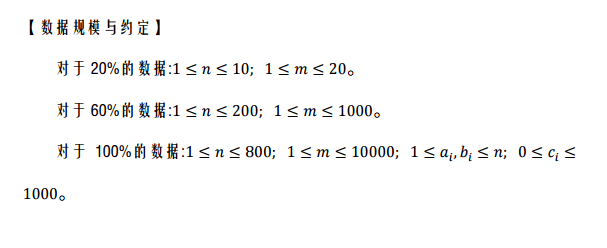
分析：

看到这个$3^i$就觉得很奇怪的样子...为什么一定要是$3^i$...而且不能重复使用...

不能重复使用就代表不会产生进位，那么一定是若干个$3^i$相加减的式子...

仔细观察，我们发现这是一个最短路径的问题，每个技能就是一条有向边，考虑要求能够用其他技能组合出来当前的技能，也就是说找到一条路径使得从当前技能的$a$出发不经过当前技能的那条边回到当前技能的$b$...这样就是说我们需要求出从每个点出发走向每个点的最短路和次短路，要求最短路和次短路的第一条边不相同...就可得到答案了...

有一个需要特别注意的点就是出现$a_i=b_i$的情况要特判一下...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
//by NeighThorn
#define inf 0x3f3f3f3f
using namespace std;

const int maxn=1600+5,maxm=20000+5;

int n,m,a[maxm],b[maxm],c[maxm],ans[maxm],del[maxm];
int cnt,w[maxm],hd[maxn],to[maxm],nxt[maxm],vis[maxn];
int dis[maxn][2],from[maxn][2]; 

inline void add(int x,int y,int s){
	w[cnt]=s;to[cnt]=y;nxt[cnt]=hd[x];hd[x]=cnt++;
}

inline void spfa(int x){
	memset(del,0,sizeof(del));
	memset(dis,inf,sizeof(dis));
	memset(from,inf,sizeof(from));
	queue<int> q;dis[x][0]=dis[x][1]=0;
	for(int i=hd[x];i!=-1;i=nxt[i]){
		if(dis[to[i]][0]>w[i]) dis[to[i]][1]=dis[to[i]][0],from[to[i]][1]=from[to[i]][0],dis[to[i]][0]=w[i],from[to[i]][0]=i;
		else if(dis[to[i]][1]>w[i]) dis[to[i]][1]=w[i],from[to[i]][1]=i;
		del[i]=1;
		if(!vis[to[i]])
			q.push(to[i]),vis[to[i]]=1;
	}
	while(!q.empty()){
		int top=q.front();q.pop();vis[top]=0;
		for(int i=hd[top],modi;i!=-1;i=nxt[i])
			if(!del[i]){
				modi=0;
				if(dis[top][0]+w[i]<dis[to[i]][0]){
					modi=1;
					if(from[to[i]][0]!=from[top][0]){
						dis[to[i]][1]=dis[to[i]][0],from[to[i]][1]=from[to[i]][0];
						dis[to[i]][0]=dis[top][0]+w[i],from[to[i]][0]=from[top][0];
					}
					else
						dis[to[i]][0]=dis[top][0]+w[i];
				}
				else if(dis[to[i]][1]>dis[top][0]+w[i]&&from[to[i]][0]!=from[top][0])
					modi=1,dis[to[i]][1]=dis[top][0]+w[i],from[to[i]][1]=from[top][0];
				if(dis[to[i]][1]>dis[top][1]+w[i]&&from[to[i]][0]!=from[top][1])
					modi=1,dis[to[i]][1]=dis[top][1]+w[i],from[to[i]][1]=from[top][1];
				if(modi&&!vis[to[i]])
					vis[to[i]]=1,q.push(to[i]);
			}
	}
	for(int i=hd[x];i!=-1;i=nxt[i])
		ans[i]=from[to[i]][0]==i?dis[to[i]][1]:dis[to[i]][0];
}

signed main(void){
	freopen("A.in","r",stdin);
	freopen("A.out","w",stdout);
	memset(hd,-1,sizeof(hd));
	scanf("%d%d",&n,&m);cnt=1;
	for(int i=1;i<=m;i++)
		scanf("%d%d%d",&a[i],&b[i],&c[i]),add(a[i],b[i]+n,c[i]);
	for(int i=1;i<=n;i++) add(i+n,i,0);
	for(int i=1;i<=n;i++) spfa(i);
	for(int i=1;i<=m;i++) printf("%d\n",ans[i]==inf?-1:ans[i]);
	return 0;
}

　　

---

By NeighThorn