【贪心算法】NO134 加油站

134. 加油站

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

示例 1:

输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

提示:

• gas.length == n
• cost.length == n
• 1 <= n <= 105
• 0 <= gas[i], cost[i] <= 104

暴力超时

public int canCompleteCircuit(int[] gas, int[] cost) {
        var len = gas.length;
        var diff = new int[len];
        var sum = 0;
        for (var i = 0; i < len; i++) {
            diff[i] = gas[i] - cost[i];
            sum += diff[i];
        }
        if (sum < 0) {
            return -1;
        }
        for (var i = 0; i < len; i++) {
            if (diff[i] < 0) {
                continue;
            }
            var j = (i + 1) % len;
            var count = diff[i];
            while (j != i) {
                count += diff[j];
                j = (j + 1) % len;
                if (count < 0) {
                    break;
                }
            }
            if (j == i) {
                return i;
            }
        }
        return -1;
    }

贪心算法解法一：

    public int canCompleteCircuit(int[] gas, int[] cost) {
        var len = gas.length;
        var sum = 0;
        var min = Integer.MAX_VALUE;
        for (var i = 0; i < len; i++) {
            sum += gas[i] - cost[i];
            min = Math.min(min, sum);
        }
        //System.out.print(min);
        if (sum < 0) {
            return -1;
        }
        if(min >= 0) {
            return 0;
        }
        for(var i = len - 1; i >= 0; i--) {
            min += gas[i] - cost[i];
            if(min >= 0) {
                return i;
            }
        }
        return -1;
    }

• 首先，从0开始迭代，找出每日剩余（gas[i] - cost[i]）的最小值min 和 和sum
• 如果sum<0则无论从哪个加油站开始都无法遍历全部
• 如果最小值min>=0则证明从0号站出发没有出现断油，返回0
• 否则则最小值为负数，从后往前查找并累加每日消耗能够填平这个负数的值，返回这个值的下标

为什么是往前查找？min记录的是从0开始到某一下标（假设为i）的消耗总和的最小值，所以想要找能够填平这个负数的下标，需要从0的前面，也就是len-1的位置开始，不断向前累加，直到出现大于等于零的下标。

min区间后是不会出现负数的，因为如果后面出现负数的话，min就会得到更新从而变得更小

贪心算法解法二：

public int canCompleteCircuit(int[] gas, int[] cost) {
        var len = gas.length;
        var curSum = 0;
        var totalSum = 0;
        var ans = 0;
        for (var i = 0; i < len; i++) {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if(curSum < 0) {
                ans = i + 1;
                curSum = 0;
            }
        }

        //System.out.print(min);
        if (totalSum < 0) {
            return -1;
        }

        return ans;
    }

算法核心思想：

​ 如果当前从0到i的累加和curSum小于零，则说明从0到i的下标均不能作为开始加油站下标，那么就让i+1尝试作为初始下标，并重置curSum为0.验证贪心算法的正确性最好的就是列举一些反例：

• i+1后会不会出现更大的负数？和前面一样，如果出现再使curSum小于0的话，就会又更新为i+1了

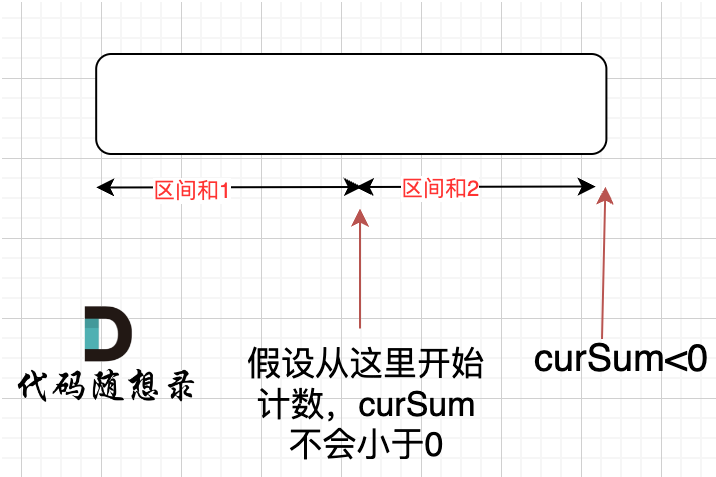
• 如果[0, i]区间选某一个中间点作为起点到i，累加到curSum是不小于零呢？

  不会的，如下图：按照上面的假设，总体curSum<0即 区间和1 + 区间和2 < 0，而区间和2>0，那么区间和1 < 0，这是不可能的，如果区间和1小于零，意味着早就该更新curSum为0了