【ACM程序设计】动态规划 第二篇 LCS&LIS问题

动态规划

P1439 【模板】最长公共子序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

给出 1,2,…,n 的两个排列 P1 和 P2 ，求它们的最长公共子序列。

输入格式

第一行是一个数 n。

接下来两行，每行为 n 个数，为自然数 1,2,…,n 的一个排列。

输出格式

一个数，即最长公共子序列的长度。

输入输出样例

输入 #1

5
3 2 1 4 5
1 2 3 4 5

输出 #1

3

说明/提示

• 对于 50% 的数据， n≤1000；
• 对于 100% 的数据， n≤100000。

首先 我们区分两个概念：

• 子序列：序列的一部分项按原有次序排列而得的序列，也是说 这里 如 3 1 5 也算子序列
• 子串：串的连续一部分
• 排列：从1~n不重复出现

这题如何用dp来解决？首先，我们把序列分为X和Y两个序列。

我们尝试寻找一个最优子结构和定义一个状态来表示公共子序列的大小。

于是，我们可以想到：从两个串的第一位开始逐个对比到至最后。我们定义状态d( i , j )，表示两个串 X 对比到第 i 位， Y 对比到第 j 位这个状态下的最长公共子序列，那么d(n,n)即为原题目的解。

我们可以写出状态转移方程：

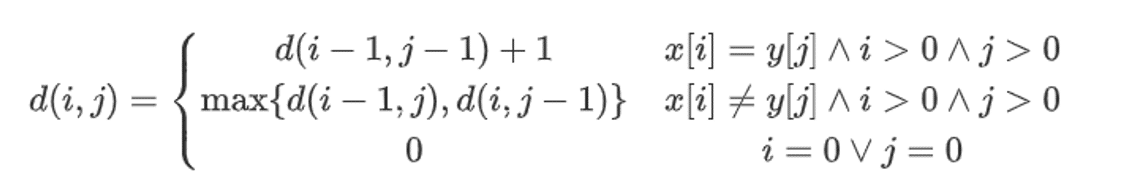
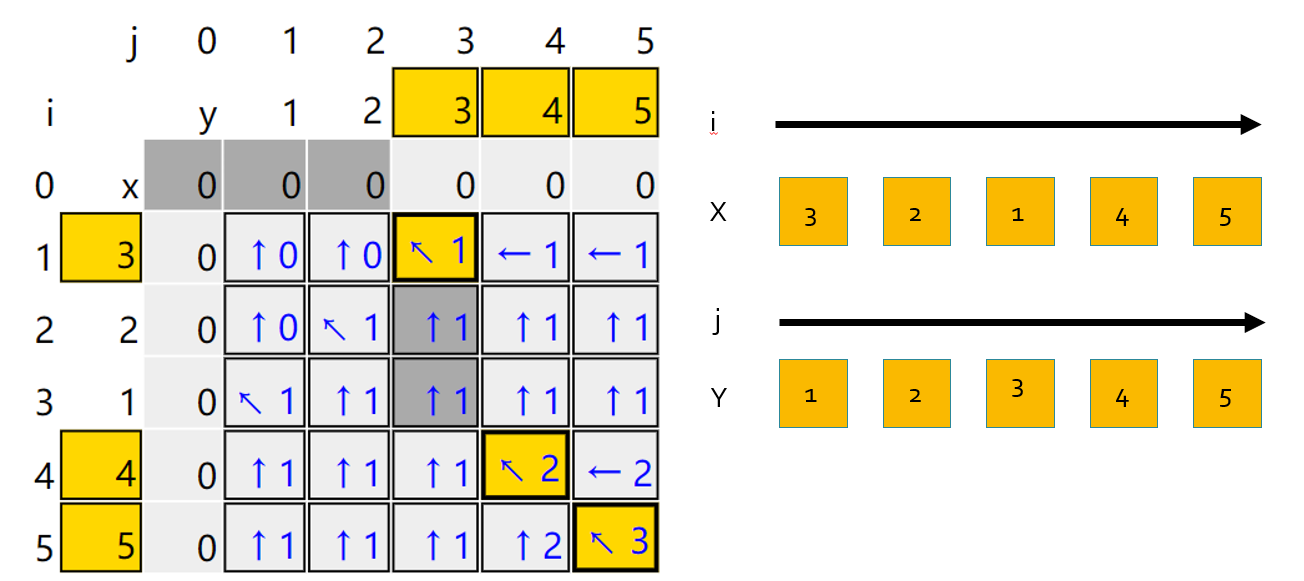
由此，我们可以写出代码：

#include<stdio.h>
const int N = 1e3 + 7; //1007
int x[N];
int y[N];
int d[N][N];
int max(int x, int y) { return x > y ? x : y; }
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &x[i]);
    for (int i = 1; i <= n; i++)
        scanf("%d", &y[i]);
    for (int i = 1; i <= n; i++)
        d[i][0] = d[0][i] = 0;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
        {
            if (x[i] == y[j])
                d[i][j] = d[i - 1][j - 1] + 1;
            else d[i][j] = max(d[i - 1][j], d[i][j - 1]);
        }
    printf("%d", d[n][n]);
    return 0;
}

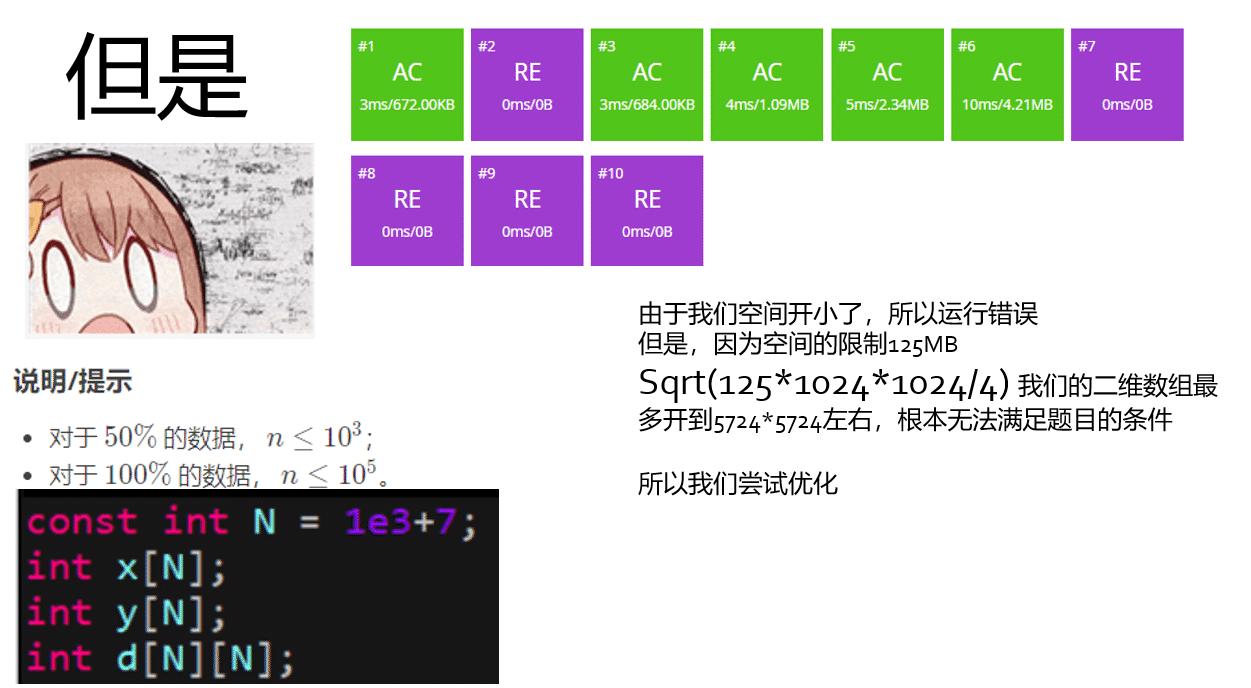
我们尝试对空间进行优化。

会发现，每次的d(I,j)都是由它左边d(I,j-1)或者上边d(i-1,j)或者左上的值转变而来。

那么我们是不是就可以用一个二维数组来滚动代替储存呢？

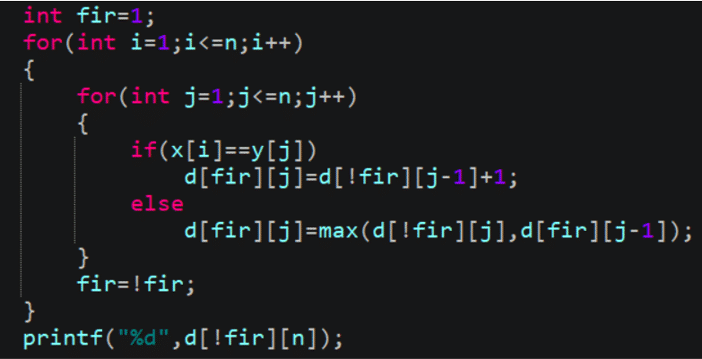
这样，我们就把第一维的空间压缩为2

由于我们循环执行的次数是n^2,所以时间复杂度是O(1e10),必定超时啊。

LCS&LIS问题

如果你能想出朴素的dp算法那你在第一层，能够用滚动数组优化空间那你在第二层，然而出题人在第五层，算法竞赛就是这样。

我们发现两个数组都是全排列数组，也就是说a中的数字在b中只会出现一次，a中没出现的数字b中也不会出现，b只是a的另一种排列顺序。

那么我们以a的顺序为基准按出现的时机进行记录后再对b中的数字按照记录标记那么b中只有出现时机单调递增的子序列是符合题目的，这就让题目从LCS问题变为了LIS问题。

LCS问题：最长公共子序列问题

LIS问题： 最长上升子序列问题

​ ind[num] = i; data[i]=ind[num];

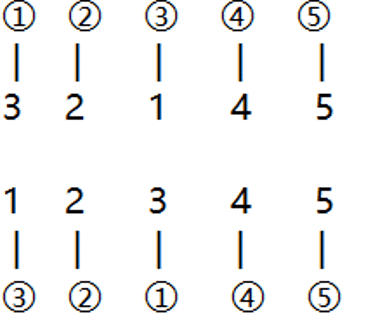
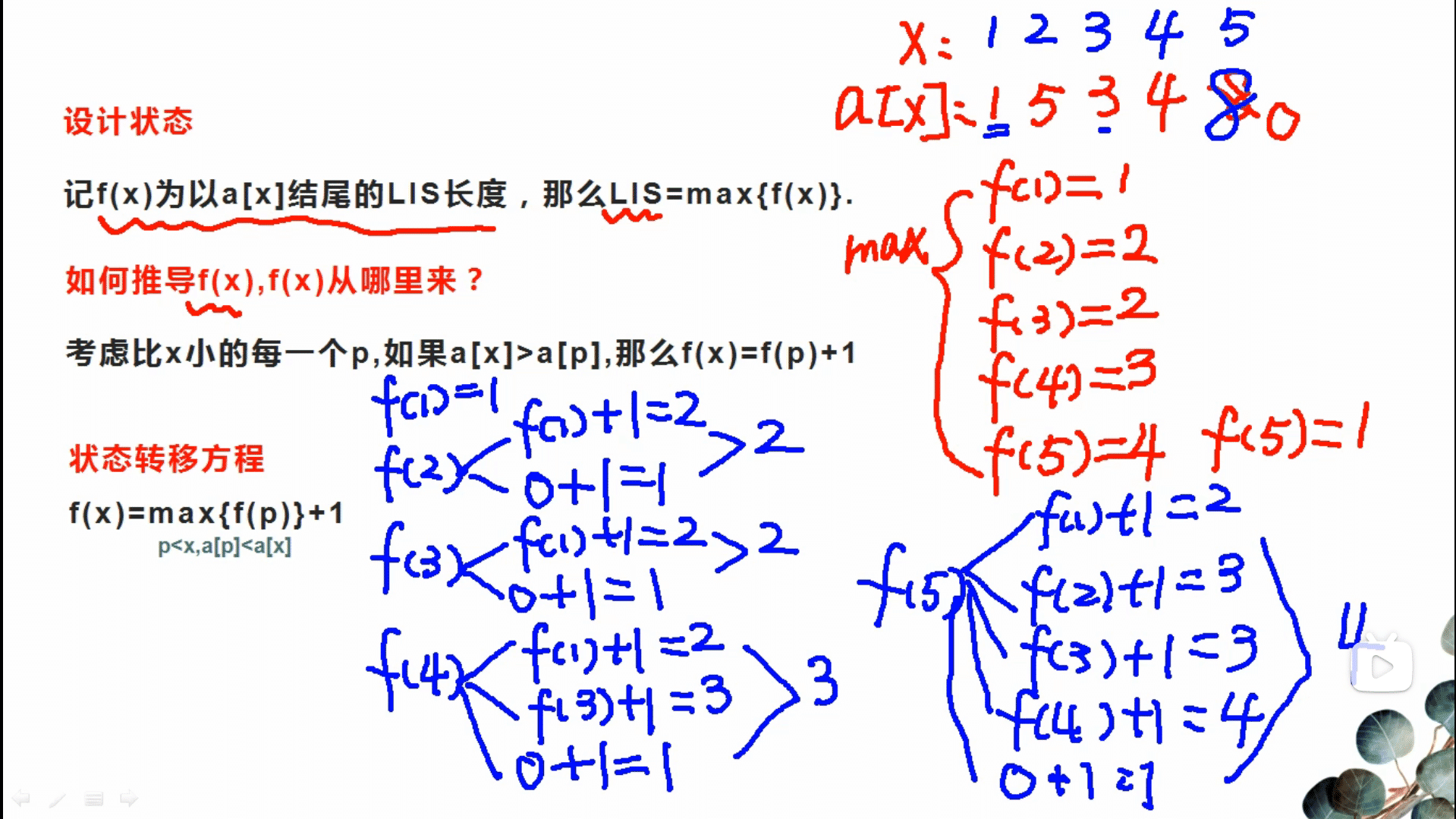
举个例子 求 1 7 6 2 3 4最长上升子序列

定义状态：d(i)表示以第i个数字结尾的最长上升子序列

状态转移：

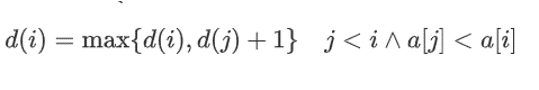
初始状态：

对于每一个数来说，最长上升序列就是本身，即d [ i ] 的初始值为1

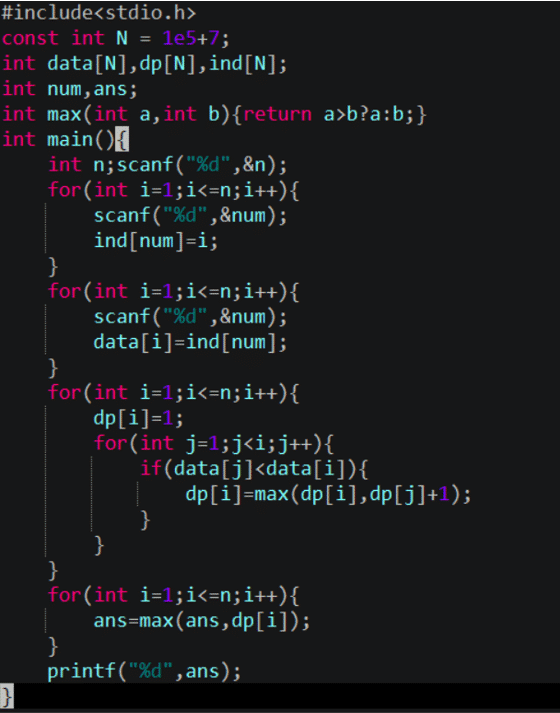
#include<stdio.h>
int a[100];
int dp[100];
int max(int x, int y) { return x > y ? x : y; }
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)
    {
        dp[i]=1;
        for(int j=1;j<i;j++)
        {
            if(a[j]<a[i])
                dp=max(dp[i],dp[j]+1);
        }
        printf("dp[%d]=%d",i,dp[i]);
    }
    return 0;
}

num 3 2 1 4 5 1 2 3 4 5

ind[3]=1,ind[2]=2,ind[1]=3,ind[4]=4,ind[5]=5

data[1]=ind[1]=3,data[2]=ind[2]=2,data[3]=ind[3]=1,data[4]=ind[4]=4,data[5]=ind[5]=5

dp[1]=1 i=2 j=1 data[1]>data[2]，dp[2]=1 i=3 j=1 dp[3]=1 j=2 dp[3]=1

i=4 j=1 dp[4]=max(dp[4],dp[1]+1)=2 j=2 dp[4]=2

i=5 j=1 dp[5]=3

ans=3

但是 时间还是n^2

1 7 6 2 3 4

为了优化，我们可以另外开一个单调的数组，用于储存上升的数。

设置一个答案序列B，初始为空。第一次搜索到了1，将1加入答案序列，然后到了7，7>1故加入序列，随后到

了数字6，我们找到序列中第一个大于该数字的数，用该数字进行替换。

这是因为我们只需要求出长度，这样子替换不会对最终的答案造成影响可以视为答案序列被替换后的6即表示原序列6的位置，也表示7的位置。

最终答案序列是{1,2(6,7),3,4}

假如是5 2 3 1 4，最终答案序列是{1(2,5),3,4} 可以看出1的位置能够表示2或者5，最终序列的答案也是2,3,4。

由于该队列的严格单调，所以我们使用二分的方法去查找。

最后的答案即队列的长度。

1,7,6,2,3,4

i=1 {1}

i=2 {1,7}

i=3 {1,6(7)} 因为6比7小，覆盖了7可以使来了更大的数可以延长这个序列

i=4 {1,2(6,7)} 同理，其作用在下一行表现出来了

i=5 {1,2(6,7),3}

i=6 {1,2(6,7),3,4}

答案为4。

#include<stdio.h>
const int N = 1e5 + 7;
int data[N], dp[N], ind[N];
int goal[N]; //队列
int num, ans;
int max(int x, int y) { return x > y ? x : y; }
//二分查找
int search(int l, int r, int num)
{
    while (l < r)
    {
        int mid = (l + r) >> 1;
        if (num <= goal[mid]) r = mid;
        else l = mid + 1;
    }
    return l;
}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &num);
        ind[num] = i;
    }
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &num);
        data[i] = ind[num];
    }
    int len = 1;
    goal[1] = data[1];
    int pos = 0;
    for (int i = 2; i <= n; i++)
    {
        //data[i]>队尾元素故加入序列
        if (goal[len] < data[i])
            goal[++len] = data[i];
        //查找到第一个大于data[i]的数，用该数字进行替换
        else
            goal[search(1, len, data[i])] = data[i];
    }
    printf("%d", len);
    return 0;
}

这样我们的时间可以化为O(n*log n)