Sliding Window - 题解【单调队列】

题面：

An array of size n ≤ 10⁶ is given to you. There is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves rightwards by one position. Following is an example:
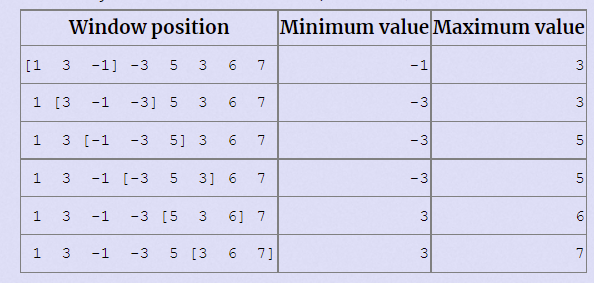
The array is [1 3 -1 -3 5 3 6 7], and k is 3.

Your task is to determine the maximum and minimum values in the sliding window at each position.

Input

The input consists of two lines. The first line contains two integers n and k which are the lengths of the array and the sliding window. There are n integers in the second line.

Output

There are two lines in the output. The first line gives the minimum values in the window at each position, from left to right, respectively. The second line gives the maximum values.

 

Sample Input

8 3
1 3 -1 -3 5 3 6 7

Sample Output

-1 -3 -3 -3 3 3
3 3 5 5 6 7

大意：

给定一个序列，有一个长度为 k 的滑动窗口，当这个窗口从左往右移动的过程中，输出每一个位置窗口内的数的最大值与最小值。

题解：

一开始，我看题面给出的时间限制是15000ms——15秒？？？再看一下10e6的数据范围，我当时就手打了一个O(n²)的程序交了上去，结果可想而知，果断地TLE了qaq……

后来一想，这是放在数据结构专题的练习题，肯定是需要一些特殊的结构来完成，答案就是这篇博文的主角：单调队列。

所谓单调队列，就是内部的元素具有单调性的队列。以求区间最小值为例，我们需要一个单调不减序列，待处理的元素从队列的尾部进入，每一次新元素进入之前，都和队列尾部的元素做个比较，如果尾部的元素比待进入的元素还要大的话，队列内的元素就从尾部出队，然后再次进行比较，直到遇到队列尾元素小于等于待进入元素为止。在读入k个元素以后，每次元素从尾部进入（窗口右移），不在窗口范围内的元素就要从队首出队，同时由于单调不减的性质，队列的最前一项就是该区间内的最小值。根据单调队列有元素需要从尾部弹出的这个特性，我们需要使用双端队列来实现，在C++ STL 中有一个容器deque可以满足我们的需求。下面的代码段中，m[i]存放读入的数据，que为构造的单调不减队列。

rep(i, 1, n) {//for(int i=1,i<=n;++i)
	while (!que.empty() && que.back() > m[i]) {
		que.pop_back();
		num.pop_back();//在这里我们需要记录下每一个元素的索引，来判断窗口移动过程中是否需要出队
	}
	que.push_back(m[i]);
	num.push_back(i);
	if (num.front() < i - k + 1) {
		que.pop_front();
		num.pop_front();//进行出队操作
	}
	if (i >= k) {
		printf("%d ", que.front());//输出队列头部元素（由单调队列性质，一定是最小值）
	}
}

以题目的数据做个示例：

对于序列 [ 1 , 3 , -1 , -3 , 5 , 3 , 6 , 7 ]：

1）que序列为空，我们读入一个数字1 ，并且在 num 队列中记下索引1。

2）下一步，读入数字3 。3比此时的队列尾1还要大，满足单调不减，入队，同时记下对应的索引2。

3）接下来读入数字-1 。此时队列尾部元素3比-1小，不满足单调不减的性质，也就是说在-1存在的情况下，3不可能是这个区间内最小的元素了，所以我们把3这个元素从que队列中请出去（同时包括 num 队列中对应的索引2）。接下来的元素1同理。这时，que成了空队列，我们让-3和索引3分别入队。循环进行到第3轮，样例中k=3，所以我们开始输出前3个元素“窗口”（1，3，-1）内的最小元素，就是-1 。

4）读入-3，弹出-1，存入-3 。第二轮“窗口”（3，-1，-3）内的元素最小值就是-3 。

5）读入5，队列内满足单调不减性质。第三轮最小值仍是队首元素-3。

6）读入3，弹出5，留下3。此时的最小值还是队首的-3 。

7）读入6。这个时候循环进行到第7轮，窗口的最右边元素索引是7，窗口长度为3，也就是说此时窗口内应该是索引 [5，6，7] 的元素。虽然此时队列还是满足单调不减性质，但是队首元素-3的索引是4，不在窗口的范围内 （num.front() < i-k+1），因此我们让元素-3从队首出队。现在知道为什么我们要同时记下索引了吧~这时候队列内的元素为 [ 3 , 6 ]，最小值为队首的3。

8）读入7，满足单调队列的性质，入队，队首3索引在窗口范围内，所以最小为队首的3。循环到此结束。

每个窗口区间的最大值同理，只需把判断是否比尾部元素小改为是否比尾部元素大，构造单调不增序列就可以啦。

下面是完整的AC代码：

#include <iostream>
#include <cstdio>
#include <climits>
#include <deque>
#include <algorithm>
#define grp int T;cin>>T;while(T--)
#define elif else if
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define rrep(i,a,b) for(int i=a;i>=b;--i)
using namespace std;
typedef long long ll;

int n, k;
int m[1000010];
deque<int> que;
deque<int> num;

int main() {

	scanf("%d %d", &n, &k);
	rep(i, 1, n) {
		scanf("%d", &m[i]);
	}
	rep(i, 1, n) {
		while (!que.empty() && que.back() > m[i]) {
			que.pop_back();
			num.pop_back();
		}
		que.push_back(m[i]);
		num.push_back(i);
		if (num.front() < i - k + 1) {
			que.pop_front();
			num.pop_front();
		}
		if (i >= k) {
			printf("%d ", que.front());
		}
	}
	putchar('\n');
	que.clear();
	num.clear();
	rep(i, 1, n) {
		while (!que.empty() && que.back() < m[i]) {
			que.pop_back();
			num.pop_back();
		}
		que.push_back(m[i]);
		num.push_back(i);
		if (num.front() < i - k + 1) {
			que.pop_front();
			num.pop_front();
		}
		if (i >= k) {
			printf("%d ", que.front());
		}
	}
	putchar('\n');
	return 0;
}