UVA 1401 Remember the Word（用Trie加速动态规划）

Remember the Word

Neal is very curious about combinatorial problems, and now here comes a problem about words. Knowing that Ray has a photographic memory and this may not trouble him, Neal gives it to Jiejie.

Since Jiejie can't remember numbers clearly, he just uses sticks to help himself. Allowing for Jiejie's only 20071027 sticks, he can only record the remainders of the numbers divided by total amount of sticks.

The problem is as follows: a word needs to be divided into small pieces in such a way that each piece is from some given set of words. Given a word and the set of words, Jiejie should calculate the number of ways the given word can be divided, using the words in the set.

Input

The input file contains multiple test cases. For each test case: the first line contains the given word whose length is no more than 300 000.

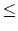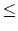The second line contains an integer S <tex2html_verbatim_mark>, 1S4000 <tex2html_verbatim_mark>.

Each of the following S <tex2html_verbatim_mark>lines contains one word from the set. Each word will be at most 100 characters long. There will be no two identical words and all letters in the words will be lowercase.

There is a blank line between consecutive test cases.

You should proceed to the end of file.

Output

For each test case, output the number, as described above, from the task description modulo 20071027.

Sample Input

abcd
4
a
b
cd
ab

Sample Output

Case 1: 2

题目大意：背单词。给出一个由S个不同单词组成的字典和一个长字符串。把这个字符串分解成若干个单词的连接（单词可以重复使用），有多少种方法？比如，有4个单词a,b,cd,ab,则abcd有两种分解方法：a+b+cd和ab+cd.

分析：不难想到这样的递推法：令d(i)表示从字符i开始的字符串（即后缀S[i..L]）的分解方案数，则d(i)=sum{d(i+len(x))|单词x是S[i..L]的前缀}。
　　如果先枚举x，再判断它是否为S[i..L]的前缀，时间无法承受（最多可能有4000个单词，判断还需要一定的时间）。可以换一个思路，先把所有单词组织成Trie，然后试着在Trie中“查找”S[i..L]。查找过程中每经过一个单词结点，就找到一个上述状态转移方程中的x，最多只需要比较100次就能能找到所有的x。

代码如下：

 #include<cstring>
 #include<vector>
 using namespace std;

 const int maxnode =  *  + ;
 const int sigma_size = ;

 // 字母表为全体小写字母的Trie
 struct Trie {
   int ch[maxnode][sigma_size];
   int val[maxnode];
   int sz; // 结点总数
   void clear() { sz = ; memset(ch[], , sizeof(ch[])); } // 初始时只有一个根结点
   int idx(char c) { return c - 'a'; } // 字符c的编号

   // 插入字符串s，附加信息为v。注意v必须非0，因为0代表“本结点不是单词结点”
   void insert(const char *s, int v) {
     int u = , n = strlen(s);
     for(int i = ; i < n; i++) {
       int c = idx(s[i]);
       if(!ch[u][c]) { // 结点不存在
         memset(ch[sz], , sizeof(ch[sz]));
         val[sz] = ;  // 中间结点的附加信息为0
         ch[u][c] = sz++; // 新建结点
       }
       u = ch[u][c]; // 往下走
     }
     val[u] = v; // 字符串的最后一个字符的附加信息为v
   }

   // 找字符串s的长度不超过len的前缀
   void find_prefixes(const char *s, int len, vector<int>& ans) {
     int u = ;
     for(int i = ; i < len; i++) {
       if(s[i] == '\0') break;
       int c = idx(s[i]);
       if(!ch[u][c]) break;
       u = ch[u][c];
       if(val[u] != ) ans.push_back(val[u]); // 找到一个前缀
     }
   }
 };

 #include<cstdio>
 const int maxl =  + ; // 文本串最大长度
 const int maxw =  + ;   // 单词最大个数
 const int maxwl =  + ;   // 每个单词最大长度
 const int MOD = ;

 int d[maxl], len[maxw], S;
 char text[maxl], word[maxwl];
 Trie trie;

 int main() {
   int kase = ;
   while(scanf("%s%d", text, &S) == ) {
     trie.clear();
     for(int i = ; i <= S; i++) {
       scanf("%s", word);
       len[i] = strlen(word);
       trie.insert(word, i);
     }
     memset(d, , sizeof(d));
     int L = strlen(text);
     d[L] = ;
     for(int i = L-; i >= ; i--) {
       vector<int> p;
       trie.find_prefixes(text+i, L-i, p);
       for(int j = ; j < p.size(); j++)
         d[i] = (d[i] + d[i+len[p[j]]]) % MOD;
     }
     printf("Case %d: %d\n", kase++, d[]);
   }
   return ;
 }