Ex 6_17 数量无限的硬币兑换问题_第七次作业

子问题定义:定义一个数组b,大小比兑换价格的大小多一个元素，其中b[i]表示是否能用面值为x1，x2，x3,..,xn的硬币兑换价格i。

递归关系:

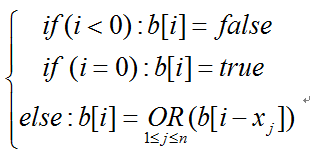
初值设定：设b[0]=true

求解顺序：按下标从小到大依次求解b[i]的值，最后返回b[v]中的结果即为最终结果。

 package org.xiu68.ch06.ex7;

 public class Ex6_17 {

     //数量无限的面值为x1,x2,x3,...,xn的硬币是否能兑换价格v
     public static void main(String[] args) {
         // TODO Auto-generated method stub
         int[] coin=new int[]{5,6};
         for(int i=0;i<=30;i++)
             convertChange(coin,i);
     }

     //coin:硬币面值
     //v:要兑换的价格
     public static void convertChange(int[] x,int v){
         boolean b[]=new boolean[v+1];    //能否用硬币兑换价格v
         b[0]=true;                        

         for(int i=1;i<=v;i++){            //能否用硬币兑换价格i (子问题的规模)
             for(int j=0;j<x.length;j++){
                 if(i>=x[j] && b[i-x[j]]==true){
                     b[i]=true;
                     break;
                 }else{
                     b[i]=false;
                 }
             }
         }
         System.out.println(v+":"+b[v]);
     }

     //运行结果
 /*    0:true
     1:false
     2:false
     3:false
     4:false
     5:true
     6:true
     7:false
     8:false
     9:false
     10:true
     11:true
     12:true
     13:false
     14:false
     15:true
     16:true
     17:true
     18:true
     19:false
     20:true
     21:true
     22:true
     23:true
     24:true
     25:true
     26:true
     27:true
     28:true
     29:true
     30:true*/
 }