bzoj 3730: 震波 动态点分治_树链剖分_线段树

##### 题目描述 ：

在一片土地上有N个城市，通过N-1条无向边互相连接，形成一棵树的结构，相邻两个城市的距离为1，其中第i个城市的价值为value[i]。
不幸的是，这片土地常常发生地震，并且随着时代的发展，城市的价值也往往会发生变动。
接下来你需要在线处理M次操作：
0 x k 表示发生了一次地震，震中城市为x，影响范围为k，所有与x距离不超过k的城市都将受到影响，该次地震造成的经济损失为所有受影响城市的价值和。
1 x y 表示第x个城市的价值变成了y。
为了体现程序的在线性，操作中的x、y、k都需要异或你程序上一次的输出来解密，如果之前没有输出，则默认上一次的输出为0

#### 题解：
第一道动态点分治题
感觉所有点分治的题的大体思路是这样的：
先假定原树的树高是 $O(logn)$ 级别，并思考在原树中怎么做。
想出来在原树中的做法后再进行一遍点分治来进行优化。
而本题中，我们不仅仅需要点分治，而是动态点分治。
首先，考虑对每个点开一颗以距离为下标，价值为权值的线段树，维护的是以该点为树根，该点子树中的节点相对与它的距离以及权值。

注：下文中提到的树均为原树，而非点分树（一会我们再会说用动态点分治优化）

考虑修改操作（对 $x$ 进行修改）
直接修改似乎有些困难，可以转换成对 $x$ 加上 $new(x)-old(x)$

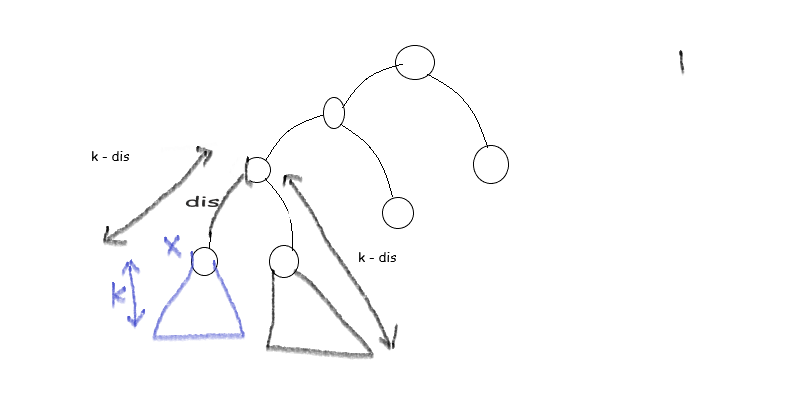
一步步跳父亲，修改 [0  dis-k] 的的所有权值，然而这么做会有上图中的问题：

由祖先向修改点会延申 $dis-k$ 的距离，这一部分是完全多余的。

于是，我们对每个点再开一颗线段树，以该点子树中到父亲距离为下标，维护权和。

考虑统计答案：

边向上跳边加上 $dis-k$ 的贡献，同时还要减掉那一部分多余的贡献。

Code:

#include<bits/stdc++.h>
#define setIO(s) freopen(s".in","r",stdin)
#define maxn 3011111
#define N 200010
#define inf 0x7f7f7f
using namespace std;
int hd[N],nx[N],to[N],cnt;
int n,m,val[N],vis[N];
void add(int u,int v)
{
    nx[++cnt]=hd[u],hd[u]=cnt,to[cnt]=v;
}
namespace heavyedge{
    int dep[N],hson[N],fa[N],siz[N],top[N];
    void dfs1(int u,int ff)
    {
        dep[u]=dep[ff]+1,fa[u]=ff,siz[u]=1;
        for(int i=hd[u];i;i=nx[i])
            if(to[i]!=ff)
            {
                dfs1(to[i],u),siz[u]+=siz[to[i]];
                if(siz[to[i]]>siz[hson[u]]) hson[u]=to[i];
            }
    }
    void dfs2(int u,int tp)
    {
        top[u]=tp;
        if(hson[u]) dfs2(hson[u],tp);
        for(int i=hd[u];i;i=nx[i])
        {
            if(to[i]==fa[u]||to[i]==hson[u]) continue;
            dfs2(to[i],to[i]);
        }
    }
    int LCA(int u,int v)
    {
        while(top[u]!=top[v]) dep[top[u]] < dep[top[v]] ? v = fa[top[v]] : u = fa[top[u]];
        return dep[u] < dep[v] ? u : v;
    }
    int main()
    {
        dfs1(1,0), dfs2(1,1);
        return 0;
    }
};
int Dis(int u,int v)
{
    return heavyedge::dep[u] + heavyedge::dep[v] - (heavyedge::dep[heavyedge::LCA(u,v)] << 1);
}
int siz[N],f[N],root,sn,Fa[N];
int GetRoot(int u,int ff)
{
    siz[u] = 1,f[u] = 0;
    for(int i = hd[u]; i ; i = nx[i])
    {
        if(to[i] == ff || vis[to[i]]) continue;
        GetRoot(to[i],u);
        siz[u] += siz[to[i]];
        f[u] = max(f[u],siz[to[i]]);
    }

    f[u] = max(f[u],sn - siz[u]);
    if(f[u] < f[root]) root = u;
}
void dfs(int u)
{
    vis[u] = 1;
    for(int i = hd[u]; i ; i = nx[i])
    {
        if(vis[to[i]]) continue;
        root = 0, sn = siz[to[i]], GetRoot(to[i],u);
        Fa[root] = u, dfs(root);
    }
}
struct Segment_Tree{
    int tot;
    struct Node
    {
        int l,r,v;
    }t[maxn<<1];
    void update(int &o,int l,int r,int p,int w)
    {
        if(!o) o = ++tot;
        t[o].v += w;
        if(l == r) return;
        int mid = (l + r) >> 1;
        if(p <= mid) update(t[o].l,l,mid,p,w);
        else update(t[o].r,mid + 1,r,p,w);
    }
    int query(int o,int l,int r,int L,int R)
    {
        if(!o || l > r) return 0;
        if(l >= L && r <= R) return t[o].v;
        int ret = 0, mid = (l + r) >> 1;
        if(L <= mid) ret += query(t[o].l,l,mid,L,R);
        if(mid + 1 <= R) ret += query(t[o].r,mid + 1,r,L,R);
        return ret;
    }
}T;
int ans = 0,rt[N];
#define fax(x) (x + n)
int Query(int x,int k)
{
    int ret = T.query(rt[x],0,n,0,k);
    for(int i = x; Fa[i] ; i = Fa[i])
    {
        int dis = Dis(x, Fa[i]);
        if(dis > k) continue;
        ret += T.query(rt[Fa[i]],0,n,0,k - dis);
        ret -= T.query(rt[fax(i)],0,n,0,k - dis);
    }
    return ret;
}
void Update(int x,int k)
{
    T.update(rt[x],0,n,0,k);
    for(int i = x; Fa[i]; i = Fa[i])
    {
        int dis = Dis(x, Fa[i]);               //正确性显然
        T.update(rt[Fa[i]],0,n,dis,k);
        T.update(rt[fax(i)],0,n,dis,k);
    }
}
int main()
{
    // setIO("input");
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n; ++i) scanf("%d",&val[i]);
    for(int i = 1,u,v;i < n; ++i)  scanf("%d%d",&u,&v), add(u,v),add(v,u);
    heavyedge :: main();
    f[0] = inf, sn = n,root = 0,GetRoot(1,0), dfs(root);
    for(int i = 1;i <= n; ++i) Update(i,val[i]);
    while(m--)
    {
        int x,y,opt;
        scanf("%d%d%d",&opt,&x,&y);
        x ^= ans, y ^= ans;
        if(opt == 0)  printf("%d\n",ans = Query(x,y));
        if(opt == 1)  Update(x,y-val[x]),val[x]=y;
    }

    return 0;
}