poj 1410 Intersection (判断线段与矩形相交 判线段相交)

题目链接

Intersection

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 12040		Accepted: 3125

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example: 
line: start point: (4,9) 
end point: (11,2) 
rectangle: left-top: (1,5) 
right-bottom: (7,1)

 
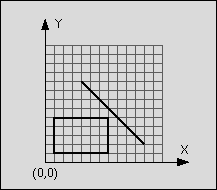
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format: 
xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

题意：

有一个矩阵是实心的，给出一条线段，问线段和矩阵是否相交

分析：有很多坑点，

①给出的矩形顶点的坐标需要自己重新排下序再使用，看discuss说所谓的top等并不是严格指上方，只是一个相对的参考，所以要重新排下序再用。

②因为题目里面说了矩形的内部也算矩形的一部分，所以线段在矩形内部是认为和矩形相交的。

③在判断线段与矩形四个边是否有交点时，要注意对非规范相交的判定，当线段和边共线且不相交时叉积也为0。

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cstdlib>
 #include <cmath>
 #include <algorithm>
 #define LL __int64
 const int maxn = 1e2 + ;
 const double eps = 1e-;
 using namespace std;

 struct node
 {
     double x, y;
 }l1, l2, a, b, c, d;

 double mult(node a, node b, node c) //叉积
 {
     return ((b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y));
 }
 bool solve() //判断点在矩形里
 {
     if((l1.x>=a.x && l1.x<=b.x && l1.y>=d.y && l1.y<=a.y) || (l2.x>=a.x && l2.x<=b.x && l2.y>=d.y && l2.y<=a.y))
     return true;
     return false;
 }
 bool solve2(node a, node b, node c, node d) //判断线段ab与线段cd是否相交，相交返回true,包含线段重合的情况，已测试。
 {
     if(max(a.x, b.x)<min(c.x, d.x)) return false;
     if(max(a.y, b.y)<min(c.y, d.y)) return false;
     if(max(c.x, d.x)<min(a.x, b.x)) return false;
     if(max(c.y, d.y)<min(a.y, b.y)) return false;
     if(mult(c, d, a)*mult(c, d, b)>)
         return false;
     if(mult(a, b, c)*mult(a, b, d)>)
        return false;
     return true;
 }
 int main()
 {
     int n;
     scanf("%d", &n);
     int xx = ;
     while(n--)
     {
         scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &l1.x, &l1.y, &l2.x, &l2.y, &a.x, &a.y, &c.x, &c.y);
         if(a.x > c.x) {
             b.x = a.x;
             d.x = c.x;
         }
         else {
             b.x = c.x;
             d.x = a.x;
         }
         if(a.y > c.y) {
             b.y = a.y;
             d.y = c.y;
         }
         else {
             b.y = c.y;
             d.y = a.y;
         }
         a.x = d.x; a.y = b.y;
         c.x = b.x; c.y = d.y;
         if(solve())
             cout<<"T"<<endl;
         else if(solve2(l1, l2, a, b)||solve2(l1, l2, a, d)||solve2(l1, l2, c, b)||solve2(l1, l2, c, d))
         cout<<"T"<<endl;
         else cout<<"F"<<endl;
     }
     return ;
 }