数据结构（C#）：图的最短路径问题、（Dijkstra算法）

　　今天曾洋老师教了有关于图的最短路径问题，现在对例子进行一个自己的理解和整理：

题目：

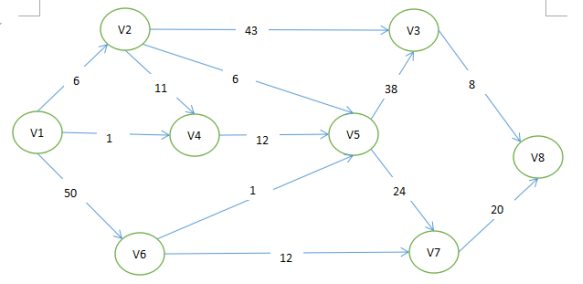
要求：变成计算出给出结点V1到结点V8的最短路径

答：

　　首先呢，我会先通过图先把从V1到V8的各种路径全部计算下来，如下：

　　（1）v1 -> v4 -> v5 -> v3 -> v8   =>  1+12+38+8=59

　　（2）v1 -> v4 -> v5 -> v7 -> v8  =>  1+12+24+20=57

　　（3）v1 -> v6 -> v5 -> v7 -> v8  =>  50+1+24+20=95

　　（4）v1 -> v6 -> v7 -> v8  =>  50+12+20=82

　　（5）v1 -> v2 -> v3 -> v8  => 6+43+8=57

　　（6）v1 -> v2 -> v5 -> v3 -> v8  =>  6+6+38+8=58

　　（7）v1 -> v2 -> v5 -> v7 -> v8  =>  6+6+24+20=56（最短路径）

　　（8）v1 -> v2 -> v4 -> v5 -> v3 -> v8  =>  6+11+12+24+20=75

　　（9）v1 -> v2 -> v4 -> v5 -> v7 -> v8  =>  6+11+12+24+20=73

从上面列出来的路径中，很清楚的看到（7）的路径数是最短的，那么，下面我们通过Dijkstra算法来确定从V1到其他数之间的最小距离分别是多少

步骤一：

先定义两个数组：

f：表示判断是否已经找到最短路径，1表示找到，0表示暂且没找到

d：表示当前最短路径

首先，从V1开始，f的第一个一定是1，因为它与它本身的距离一定是最短的（无距离）

　　　　　　　　　d的第一个一定是0，因为V1和V1无算数概念可言，

　　　　　　　　　接着V1分别与其他路径进行计算，必须是直接路径才算，不是直接路径的只能算是无穷大

　　　　　　　　　（例如题中，V1到V2的距离为6，那么在d的数组中的距离就放入6，而V1到V3没有直接到达，需要经过V2，所以只能是无穷大）

　　　　如图所示：

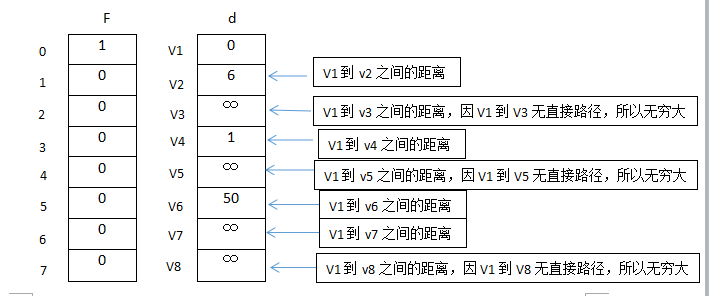
步骤二：

在输入完V1到其他数字的距离后，我们开始看d中的数字，在d的数组中，最小的数字为V4对应的1

那么，我们就把d中的V4为结点，把它相对应在f的位置从0改成1,（在f中，只要为1的，在d中相对应的数字在之后运算中都无需再改，因为它就是最短路径了）

接着，我们就可以从V1经过V4之后的所有路径进行计算了（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）

　　　　如图所示：

步骤三：

在输入V4的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V2对应的6

那么，这次我们把V6对应的数字为结点，在f中对应的0改成1

再通过V6与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）

如图所示：

步骤四：

在输入V4的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V5对应的12

那么，这次我们把V5对应的数字为结点，在f中对应的0改成1

再通过V5与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）

如图所示：

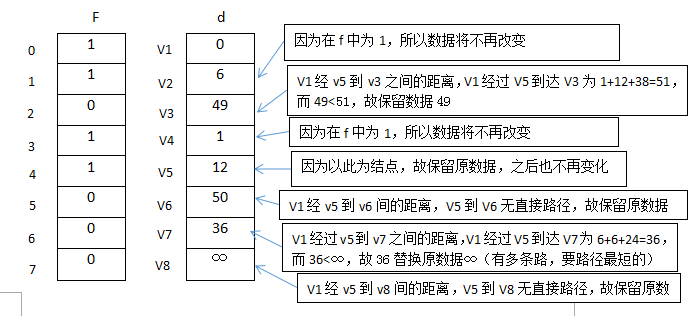
步骤五：

在输入V5的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V7对应的36

那么，这次我们把V7对应的数字为结点，在f中对应的0改成1

再通过V7与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）

如图所示：

步骤六：

在输入V7的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V3对应的49

那么，这次我们把V3对应的数字为结点，在f中对应的0改成1

再通过V3与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）

如图所示：

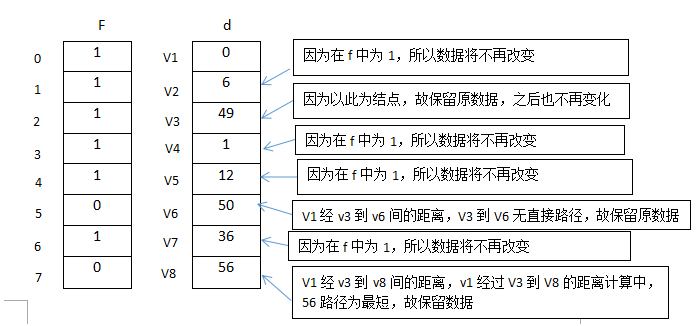
步骤七：

在输入V3的所有数据后，我们再次看d中的数字，在d的数组中，最小的数字为V6对应的50

那么，这次我们把V6对应的数字为结点，在f中对应的0改成1

再通过V6与其他在f中为0，d中相对应的数据进行路径长短计算（在计算过程中，若数据比原数据大，就保留原数据，否则替换原数据）

如图所示：

步骤八：

在输入V6的所有数据后，我们看到f数组中，只剩下了V8的数据为0，

那么，这次我们只要把V8在f中对应的0改成1，那么这次试题就结束了

如图所示：

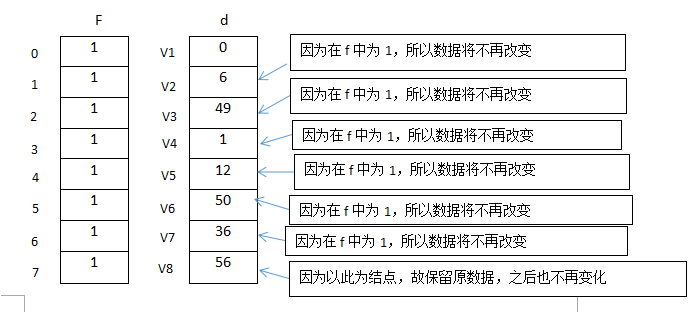
结果：

以V1为开始结点到其他的结点的最短距离分别是：

V1 -> V2  =  6

V1 -> V3  =  49

V1 -> V4  = 1

V1 -> V5  =12

V1 -> V6  = 50

V1 -> V7  =  36

V1 -> V8  = 56

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　END