P4965 薇尔莉特的打字机

题目

P4965 薇尔莉特的打字机

快到十二点了正在颓废突然发现了一道好题

虽然毒瘤，但确实是容斥原理的好题啊，做法也特别巧妙(标程

思路

题目大意(怕自己突然忘)

n个初始字符，m个操作(加入或删除)，任何一个操作都可能无效，求最后不同的字符方案数\((n,m<=5*10^6)\)

先考虑无删除操作

这里的\(t_{0..i}\)为一个字串，\(\widetilde{t_{0..i}}\)指该字串不同的子序列个数，\(dp_i\)为\(\widetilde{t_{0..i-1}}\)

若\(t_{i}\)这个字符在循环时第一次出现，即\(t_{0...i-1}\)没出现过\(t_{i}\)，显然我们考虑的状态有三种

\(~~~~~1.\widetilde{t_{0..i-1}}\)，有 \(dp_{i-1}\)个\(\Longrightarrow\)理解：插入操作无效或只考虑前面字符的方案数

\(~~~~~2.\widetilde{t_{0..i-1}} + \{t_i\}\)，有\(dp_{i-1}\)个\(\Longrightarrow\)理解：插入操作有效，且与前面字符组合起来的方案数

\(~~~~~3.\widetilde{t_{i..i}}\)\(\Longrightarrow\)理解：插入操作有效\(t_{i}\)单独组成一种方案

综上，\(t_{i}\)这个字符在循环时第一次出现：\(dp_{i}=2*dp{i-1}+1\)

\(\begin{aligned}
\\
\end{aligned}\)

那不是第一次出现呢?显然会出现重复的子序列

\(lst[c]\)表示字符\(c\) 上一次出现的位置

1.\(\widetilde{t_{0..lst[t_i]-1}}+\{t_{lst[t_i]}\}\)与\(\widetilde{t_{0..lst[t_i]-1}}+\{t_i\}\) 重复

2.\(\{t_{lst[t_i]}\}\) 与 \(\{t_i\}\) 重复

综上，\(dp_i\)要去掉\(dp_{lst[t_i]-1}+1\)

\(\therefore dp_i=\begin{cases}2*dp_{i-1}+1\quad(t_i\text{第一次出现})\\2dp_{i-1}-dp_{lst[t_i]-1}\quad (t_i\text{出现过})\end{cases}\)

目前为止，时间复杂度为\(O(m)\)，毒瘤的出题人不可能就这样放过我们嘛\(emmm\)

考虑删除操作

其实删除操作只用考虑删除前面的文本串，为什么？删除插入操作无异与：删除与插入两个操作同时无效，而前面的方程已经将此情况考虑进去了

故我们只用考虑文本串与插入操作中间的删除操作

当能作为有效删除操作为\(cnt\)个时，我们枚举有\(k(k<=cnt)\)个有效操作

则此时新增子序列\(s_{0..n-k-1} + \widetilde{t_{pre[p_k]..m-1}}\)

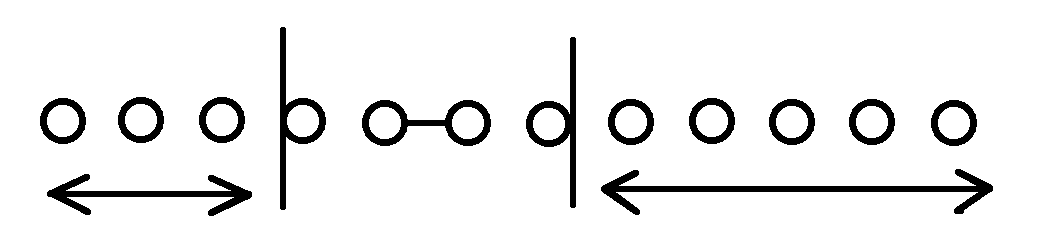
发现没有？从小到大枚举\(k\)，时间复杂度瞬间指数加\(1\)成了\(O(m^2)\)，那我们就从\(m-1\)~\(0\)逆推，又变成线性的了！！

故\(dp_i\)为\(\widetilde{t_{i..m-1}}\)，\(lst[c]\)为倒推时字符\(c\)上一次出现的位置，由于删除操作的存在，方程中的\(dp_{i-1}\) 改为\(dp_{pre[i]}\)(这些应该都好理解吧)

\(\begin{aligned}
\\
\end{aligned}\)

同样地，我们还得考虑重复部分，

若退格所删去的最后一个字符即\(s_{n-k}\)在 \(t_{pre[p_k]..m-1}\) 中出现过，则会产生重复的答案：第\(k\)删除在文本串\(s\)中删除的字符是\(s_{n-k}\)，

而在第\(k-1\) 个删除 时，\(s_{n-k}\)不会被删除，则一旦 \(s_{n-k}\) 在 \(t_{pre[p_k]..m-1}\) 中出现过，就意味着在只有\(k-1\)个删除时\(s_{n-k}\)会与后面的发生重复

重复子序列为\(s_{0..n-k}+\widetilde{t_{pre[lst[s_{n-k}]]..m-1}}\)以及\(s_{0..n-k}\)，个数为 \(dp_{pre[lst[s_{n-k}]]}+1\)，计算答案时要将这部分减去

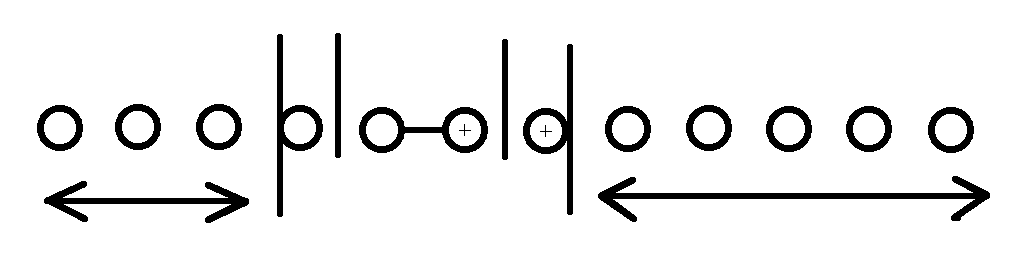
My complete code

上短得可怜的代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int p=0x125E591;
const int maxn=5000000+9;
int n,m,pos,cnt,ans;
int lst[maxn],pre[maxn],dp[maxn];
char s[maxn],t[maxn];
inline int Get(char x){
    return (lst[x])?p-dp[pre[lst[x]]]:1;
}
int main(){
    scanf("%d%d",&n,&m);
    scanf(" %s %s",s,t);
    for(int i=0;i<m;++i)
        cnt+=(t[i]=='u');
    for(int i=m-1;i>=0;--i)
    	if(t[i]=='u'){
    		if(n-cnt>=0)
                ans=(ans+dp[pos]+Get(s[n-cnt]))%p;
            --cnt;
        }else{
            dp[i]=(2*dp[pre[i]=pos]+Get(t[i]))%p;
            pos=lst[t[i]]=i;
        }
    printf("%d",(ans+dp[pos]+1)%p);
    return 0;
}

总结

动规啊容斥啊这些真的得完全弄懂再去写代码，几次想写代码了还是回过头自己纯手推了一下

能想到写篇博客竟然花了快一个多小时，凌晨一点半 其实也还早啊，睡觉