AVL树的平衡算法（JAVA实现）

1、概念：

　　AVL树本质上还是一个二叉搜索树，不过比二叉搜索树多了一个平衡条件：每个节点的左右子树的高度差不大于1。

二叉树的应用是为了弥补链表的查询效率问题，但是极端情况下，二叉搜索树会无限接近于链表，这种时候就无法体现二叉搜索树在查询时的高效率，而最初出现的解决方式就是AVL树。如下图：

2、旋转

　　说到AVL树就不得不提到树的旋转，旋转是AVL维持平衡的方式，主要有以下四种类型。

　　2.1、左左旋转

　　　　如图2-1所示，此时A节点的左树与右树的高度差为2，不符合AVL的定义，此时以B节点为轴心，AB间连线为转轴，将A节点旋转至B节点下方，由B节点的父节点变成子节点。实现所有节点的左右子树高

　　度差小于等于1。如图2-2。

　　2.2、右右旋转

　　　　右右旋转与左左旋转类似，但是动作相反，如图2-3，2-4所示，以B节点为轴心，BC间连线为轴，将C节点旋转至B下方，成为B的子节点。实现所有节点的左右子树高度差小于等于1。　　

　　　　2.3、左右旋转

　　　　　　左右旋转稍复杂一点，需要旋转两次，如果用左左旋转的方式直接旋转图2-5中的树，会变成图2-8的样子，此时B节点的左右子树高度差依然没有平衡，所以要先对2-5的树做一步处理，就是以BC为轴，

　　　　将C节点旋转至B节点的位置，如图2-6所示，此时就将树转换成了左左旋转的场景，之后使用左左旋转即可完成平衡。

　　　　2.4、右左旋转

　　　　　　右左旋转与左右旋转类似，也是旋转两次。如下图，具体细节请看下面的代码详解。

3、代码实现

　　3.1、新增

　　　　二叉树的插入不在赘述，这里只分析插入时的平衡方法。如果新增节点没有兄弟节点时会引起树的高度变化，此时需要对上层节点的平衡值进行修改，如果出现了不平衡树，则需要调用平衡方法，代码如下：

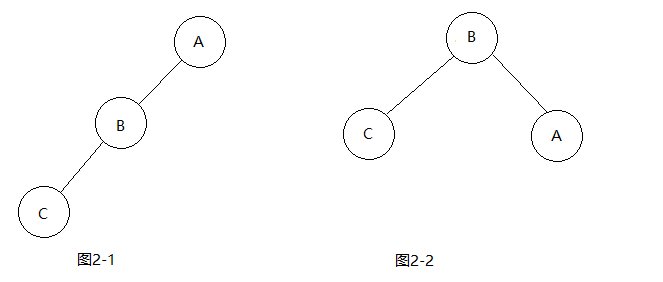
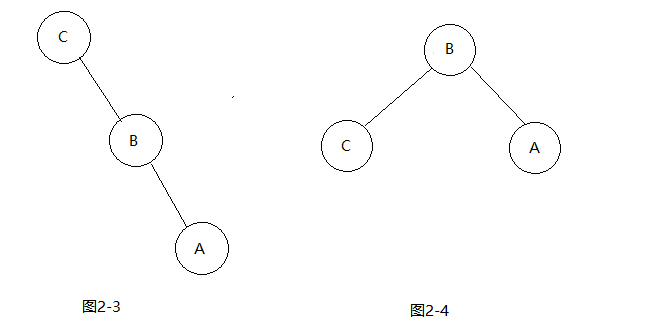
private void balance(Node node){

        Node parent = node.getParent();

        Node node_middle = node;

        Node node_prev = node;

        Boolean avl = true;

        do{

            if(node_middle == parent.getLeft() && (-1 <= parent.getAVL()-1 && parent.getAVL()-1 <= 1)){

                //node_middle为parent的左树，此时parent左树高度+1不会造成不平衡。

                parent.subAVL();

                node_prev = node_middle;

                node_middle = parent;

                //由于上面对parent的平衡值进行了修改，如果修改后的平衡值为0，说明此时parent节点的高度没有改变，之前较短的左树高度+1，变为与右树高度相同。

                if(parent != null && parent.getAVL() == 0)

                    parent = null;

                else

                    parent = parent.getParent();

            }else if(node_middle == parent.getRight() && (-1 <= parent.getAVL()+1 && parent.getAVL()+1 <= 1)){

                //node_middle为parent的右树，此时parent右树高度+1不会造成不平衡。

                parent.addAVL();

                node_prev = node_middle;

                node_middle = parent;

                //由于上面对parent的平衡值进行了修改，如果修改后的平衡值为0，说明此时parent节点的高度没有改变，之前较短的右树高度+1，变为与左树高度相同。

                if(parent != null && parent.getAVL() == 0)

                    parent = null;

                else

                    parent = parent.getParent();

            }else{//出现最小不平衡节点，新增时不需要考虑更高节点，所以直接中断循环，调用平衡方法

                avl = false;

            }

        }while(parent != null && avl);

        if(parent == null){

            return;

        }

        //选择相应的旋转方式

        chooseCalculation(parent, node_middle, node_prev);

    }

　　3.2、删除

　　　　删除较新增复杂一些，主要是因为存在一次旋转无法达到平衡效果的情况，而且删除本身也分为三种情况，分别是：

　　　　3.2.1、删除叶子节点

　　　　　　由于叶子节点没有子树，不涉及替换的问题，所以直接删除即可，如果删除节点没有兄弟节点会引起高度变化，此时依次对父级节点的平衡值做对应修改，如果出现不平衡树则要进行旋转。

　　　　3.2.2、删除节点存在一个子节点

　　　　　　此时将子节点上移，替换删除节点的位置，这个操作势必会造成所在子树的高度变化，所以需要依次对父级节点的平衡值做对应修该，如果出现不平衡树进行旋转操作。

　　　　3.2.3、删除节点存在两个子节点

　　　　　　这种情况比较复杂，由于存在两个子节点，所以不能简单的将其中一个子节点提高一级，因此需要在节点的子树中搜索一个合适的节点进行替换，之前自己构思的时候选择的是搜寻一个最长子树的最

　　　　　　接近删除节点的值的叶子节点，具体实现的时候发现需要考虑的场景太多，并不适合，参考算法导论上的思路后改成了搜寻左树的最大节点，此时只需考虑左树的情况即可。实现方法如下：

public void deleteNode(int item){

        Node node = get(item);

        if(node == null)

            return;

        Node parent = node.getParent();

        if(!node.hasChild()){//叶子节点

            if(parent == null){//删除最后节点

                root = null;

                return;

            }

            if(node.hasBrother()){//node有兄弟节点时，需要判断是否需要调用平衡方法

                if(node == parent.getLeft())

                    isBalance(node, 1);

                else

                    isBalance(node, -1);

                parent.deleteChildNode(node);

            }else{//node没有兄弟节点时，高度减一，需要进行平衡

                deleteAvl(node);

                parent.deleteChildNode(node);

            }

        }else if(node.getLeft() != null && node.getRight() == null){//有一个子节点时，将子节点上移一位，然后进行平衡即可

            if(parent == null){//删除的是根节点

                root = node;

                return;

            }

            if(node == parent.getLeft()){

                parent.setLeft(node.getLeft());

            }else{

                parent.setRight(node.getLeft());

            }

            node.getLeft().setParent(parent);

            deleteAvl(node.getLeft());

        }else if(node.getLeft() == null && node.getRight() != null){//有一个子节点时，将子节点上移一位，然后进行平衡即可

            if(parent == null){//删除的是根节点

                root = node;

                return;

            }

            if(node == parent.getRight()){

                parent.setRight(node.getRight());

            }else{

                parent.setLeft(node.getRight());

            }

            node.getRight().setParent(parent);

            deleteAvl(node.getRight());

        }

        else{//有两个子节点时，先在节点左树寻找最大节点last，然后删除last，最后将被删除节点的value替换为last的value

            Node last = findLastNode(node);

            int tmp = last.getValue();

            deleteNode(last.getValue());

            node.setValue(tmp);

        }

        node = null;//GC

    }

　　3.3、旋转

　　　　3.3.1、左左旋转　　

private void LeftLeftRotate(Node node){

        Node parent = node.getParent();

        if(parent.getParent() != null && parent == parent.getParent().getLeft()){

            node.setParent(parent.getParent());

            parent.getParent().setLeft(node);

        }else if(parent.getParent() != null && parent == parent.getParent().getRight()){

            node.setParent(parent.getParent());

            parent.getParent().setRight(node);

        }else{

            root = node;

            node.setParent(null);

        }

        parent.setParent(node);

        parent.setLeft(node.getRight());

        if(node.getRight() != null)

            node.getRight().setParent(parent);

        node.setRight(parent);

        if(node.getAVL() == -1){//只有左节点时，parent转换后没有子节点

            parent.setAVL(0);

            node.setAVL(0);

        }else if(node.getAVL() == 0){//node有两个子节点，转换后parent有一个左节点

            parent.setAVL(-1);

            node.setAVL(1);

        }//node.getAVL()为1时会调用左右旋转

    }

　　　　3.3.2、右右旋转　

private void RightRightRotate(Node node){

        Node parent = node.getParent();

        if(parent.getParent() != null && parent == parent.getParent().getLeft()){

            node.setParent(parent.getParent());

            parent.getParent().setLeft(node);

        }else if(parent.getParent() != null && parent == parent.getParent().getRight()){

            node.setParent(parent.getParent());

            parent.getParent().setRight(node);

        }else{

            root = node;

            node.setParent(null);

        }

        parent.setParent(node);

        parent.setRight(node.getLeft());

        if(node.getLeft() != null)

            node.getLeft().setParent(parent);

        node.setLeft(parent);

        if(node.getAVL() == 1){

            node.setAVL(0);

            parent.setAVL(0);

        }else if(node.getAVL() == 0){//当node有两个节点时，转换后层数不会更改，左树比右树高1层，parent的右树比左树高一层

            parent.setAVL(1);

            node.setAVL(-1);

        }

    }

　　　　3.3.3、左右旋转

private void LeftRightRotate(Node node){

        Node parent = node.getParent();

        Node child = node.getRight();

        //左右旋转时node的avl必为1，所以只需考虑child的avl

        if(!child.hasChild()){

            node.setAVL(0);

            parent.setAVL(0);

        }else if(child.getAVL() == -1){

            node.setAVL(0);

            parent.setAVL(1);

        }else if(child.getAVL() == 1){

            node.setAVL(-1);

            parent.setAVL(0);

        }else if(child.getAVL() == 0){

            node.setAVL(0);

            parent.setAVL(0);

        }

        child.setAVL(0);

        //第一次交换

        parent.setLeft(child);

        node.setParent(child);

        node.setRight(child.getLeft());

        if(child.getLeft() != null)

            child.getLeft().setParent(node);

        child.setLeft(node);

        child.setParent(parent);

        //第二次交换

        if(parent.getParent() != null && parent == parent.getParent().getLeft()){

            child.setParent(parent.getParent());

            parent.getParent().setLeft(child);

        }else if(parent.getParent() != null && parent == parent.getParent().getRight()){

            child.setParent(parent.getParent());

            parent.getParent().setRight(child);

        }else{

            root = child;

            child.setParent(null);

        }

        parent.setParent(child);

        parent.setLeft(child.getRight());

        if(child.getRight() != null)

            child.getRight().setParent(parent);

        child.setRight(parent);

    }

　　　　3.3.4、右左旋转

private void RightLeftRotate(Node node){

        Node parent = node.getParent();

        Node child = node.getLeft();

        if(!child.hasChild()){

            node.setAVL(0);

            parent.setAVL(0);

        }else if(child.getAVL() == -1){

            node.setAVL(1);

            parent.setAVL(0);

        }else if(child.getAVL() == 1){

            node.setAVL(0);

            parent.setAVL(-1);

        }else if(child.getAVL() == 0){

            parent.setAVL(0);

            node.setAVL(0);

        }

        child.setAVL(0);

        //第一次交换

        parent.setRight(child);

        node.setParent(child);

        node.setLeft(child.getRight());

        if(child.getRight() != null)

            child.getRight().setParent(node);

        child.setRight(node);

        child.setParent(parent);

        //第二次交换

        if(parent.getParent() != null && parent == parent.getParent().getLeft()){

            child.setParent(parent.getParent());

            parent.getParent().setLeft(child);

        }else if(parent.getParent() != null && parent == parent.getParent().getRight()){

            child.setParent(parent.getParent());

            parent.getParent().setRight(child);

        }else{

            root = child;

            child.setParent(null);

        }

        parent.setParent(child);

        parent.setRight(child.getLeft());

        if(child.getLeft() != null)

            child.getLeft().setParent(parent);

        child.setLeft(parent);

    }

完整代码github地址：https://github.com/ziyuanjg/AVLTree

AVL树的平衡算法（JAVA实现）的更多相关文章

AVL树的JAVA实现及AVL树的旋转算法
1,AVL树又称平衡二叉树,它首先是一颗二叉查找树,但在二叉查找树中,某个结点的左右子树高度之差的绝对值可能会超过1,称之为不平衡.而在平衡二叉树中,任何结点的左右子树高度之差的绝对值会小于等于 1. ...
AVL树（平衡二叉查找树）
首先要说AVL树,我们就必须先说二叉查找树,先介绍二叉查找树的一些特性,然后我们再来说平衡树的一些特性,结合这些特性,然后来介绍AVL树. 一.二叉查找树 1.二叉树查找树的相关特征定义二叉树查找树 ...
判断AVL树是否平衡
AVL树是高度的平衡二插搜索树,其左子树和右子树的高度之差不超过1(树中的左子树和右子树都是AVL树),维持这个高度之差就要控制它的平衡因子.那么判断一颗AVL树是否平衡就需要判断它的左子树和右子树高 ...
AVL树高度平衡的二叉查找树
1.What is AVL tree? AVL tree 是一种特殊的二叉查找树,,首先我们要在树中引入平衡因子balance,表示结点右子树的高度减去左子树的高度差(右-左),对于一棵AVL树要么它 ...
AVL树 & 重平衡概念
AVL树是有平衡条件的二叉搜索树.这个平衡条件必须容易保持,而且需要保证树的深度是O(logN). AVL=BBST 作为二叉搜索树的最后一部分,我们来介绍最为经典的一种平衡二叉搜索树:AVL树.回顾 ...
二叉树之AVL树的平衡实现(递归与非递归)
这篇文章用来复习AVL的平衡操作,分别会介绍其旋转操作的递归与非递归实现,但是最终带有插入示例的版本会以递归呈现. 下面这张图绘制了需要旋转操作的8种情况.(我要给做这张图的兄弟一个赞)后面会给出这八 ...
leecode 树的平衡判定 java
以前写过c++版本的,感觉java写的好舒心啊/** * Definition for binary tree * public class TreeNode { * int val; * TreeN ...
Java数据结构和算法(七)--AVL树
在上篇博客中,学习了二分搜索树:Java数据结构和算法(六)--二叉树,但是二分搜索树本身存在一个问题: 如果现在插入的数据为1,2,3,4,5,6,这样有序的数据,或者是逆序这种情况下的二分搜索树 ...
AVL树(三)之 Java的实现
概要前面分别介绍了AVL树"C语言版本"和"C++版本",本章介绍AVL树的Java实现版本,它的算法与C语言和C++版本一样.内容包括:1. AVL树的介绍 ...

随机推荐

[Java] JSP笔记 - Filter 过滤器
一.什么是Web过滤器 Servlet API 很久以前就已成为企业应用开发的基石,而 Servlet 过滤器则是对 J2EE 家族的相对较新的补充. Servlet 过滤器是可插入的 Web 组件, ...
JSP多文件上传到服务器
问题描述: 作为一个Java开发Web方向的程序员,很重要的一个功能,就是上传文件功能是一定要掌握的,今天整理了一下代码. 1.JSP显示界面代码和动态添加上传文件个数. <%@ page la ...
Tomcat部署web项目,如何直接通过域名访问,不加项目名称
问题:下面的问题是互联网上问得比较多的,但是显然都是同一个问题. JavaWeb项目部署到tomcat服务之后设置不需要输入项目名称即可访问? Tomcat部署web项目,如何直接通过域名访问,不加项 ...
报错com/android/dx/command/dexer/Main : Unsupported major.minor version 52.0
看着错误信息应该是从高版本换成低版本报的错误,然而我的JDK并没有变动.会像昨天走之前干了什么? 自己在AndroidStudio上倒弄自己的小项目,更新了build tools到24了删除24,e ...
多材质（Shader）实现
最近在cocos creator上打算写个U3D中shader功能的插件(能在属性面板调整shader属性). 对其中一个功能有点疑惑,就是U3D中一个渲染物体上可以挂多个材质,后来查询了下,一个物体 ...
面向对象编程（OOP）
什么是面向对象编程,对于面向对象编程与面向过程编程的解释随处可见,个人认为对面向对象编程解释最好的一个定义是:依赖倒转原则是面向对象编程的标志,面向对象编程是一种思想,无论使用哪一种编程语言,如果在编 ...
谈谈__proto__和prototype的区别
我想javascript中的原型链一直想很多初学javascript的同学感到非常的困惑,今天看了一些文章,结合自己的理解,把原型链这个东西从新来整理一下,如有不对之处,望大家帮忙指出. 首先,我们应 ...
如何在ARM中创建Express Route
很早之前就想试试Azure的express route,但是一直没有找到合适的机会,正好有个客户需要上express route,所以最近先自己研究研究,防止在做poc的时候耗费更多时间,本次场景我们 ...
Thrift的TBinaryProtocol二进制协议分析
先上张图,说明一下thrift的二进制协议是什么东东. 报文格式编码: bool类型: 一个字节的类型,两个字节的字段编号,一个字节的值(true:1,false:0). Byte类型: 一个字节的类 ...
doT.js
最近用到的数据模板引擎有很多,今天讲的doT.js也是其中一种. doT.js的特点是体积小,速度快,并且不依赖其他插件. 官网下载:http://olado.github.io 下面是用法: 模板引 ...

AVL树的平衡算法（JAVA实现）

AVL树的平衡算法（JAVA实现）的更多相关文章

随机推荐

热门专题