Egret入门学习日记 --- 第二篇 （书籍的选择 && 书籍目录 && 书中 3.3 节 内容）

第二篇 （书籍的选择 && 书籍目录 && 书中 3.3 节 内容）

　　既然选好了Egret，那我就要想想怎么学了。

　　　　开始第一步，先加个Q群先，这不，拿到了一本《Egret  HTML5游戏开发指南》，阅至三章，得到印象相对较深的好处和坏处：

　　　　　　好处：

　　　　　　　　1、原来 Egret 这么牛皮，他们的 Egret Runtime 从底层访问OpenGL接口，让HTML5游戏和原生APP游戏，性能差别不到5帧。媲美原生了！

　　　　　　　　2、了解了WebGL技术原来是搞3D游戏用的

　　　　　　　　3、了解了Egret版本号的变迁规则

　　　　　　　　

　　　　　　坏处：

　　　　　　　　1、书中内容老旧，2016年的Egret和现在的简直天差地别，根本没法一边看一边操作。

　　　　　　　　2、我边看边总结做笔记，但是才看到第三章，各种内容和现在不一致。所以，我做笔记到第三章，就做不下去了。

　　　　　　　　

　　　　我懵逼了，《Egret  HTML5游戏开发指南》这本书不管用怎么办？接着我就百度找Egret入门。搜索到了这本《Egret引擎基础入门》，百度阅读卖20多人民币。

　　　　吸收了上次的教训，我这回先看看这本书新不新。　　

　　　　

　　　　嗯，相对2016年的《Egret  HTML5游戏开发指南》，这本《Egret引擎基础入门》更加新一些，而且作者还是有在更新的。

　　　　并且作者也有在2月份时，有回复读者的评论，感觉挺靠谱。

　　　　　

　　　　但是！小心使得万年船，我先试读一下书中的内容先！

　　　　

　　　　哥哥，我就是从那本书过来你这里的。你又叫我回去？不回！打死不回！

　　　　

　　　　哦？我瞅瞅现在Egret的版本到多少了。

　　　　

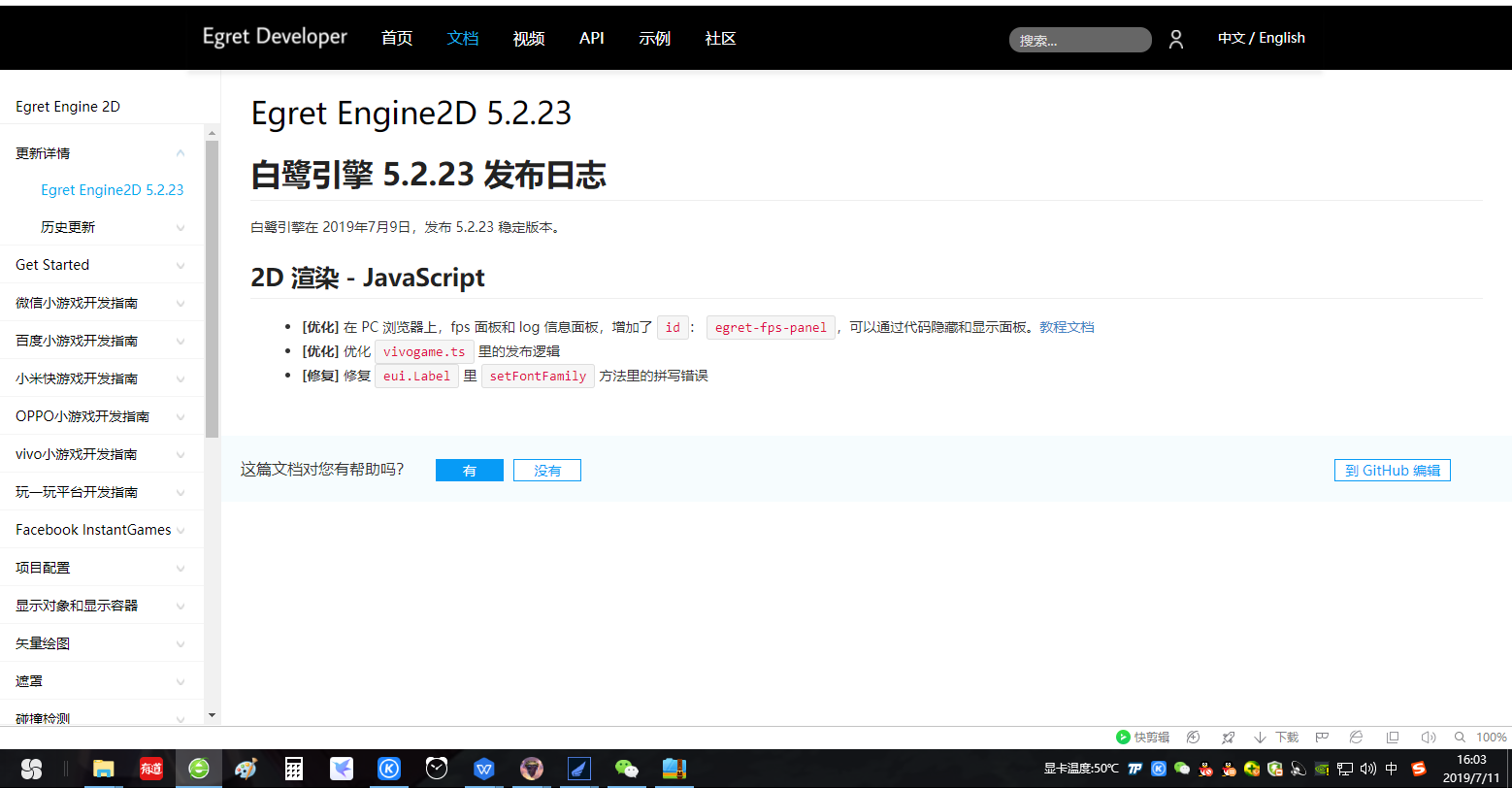
　　　　嗯，现在版本也才5.2.23, 说明《Egret引擎基础入门》这本书还是比较新的。

　　　　那么就开始可以买这本书了，是的，我买了。买了之后。。。。。。我就后悔了。

　　　　作者还能退款吗？

　　　　主要是《Egret引擎基础入门》这本书，前言作者是更新了，估计就更新写了个版本号。。。。。。但是之后的到了第三章的内容，就不同了，和现在的白鹭根本不一样。

　　　　这是书中的内容：

　　　　　　Main.ts是入口文件

　　　　　　

　　　　然而我现在看到的Main.ts是长这个样子的：

　　　　　　

　　　　这还是我偶然间去看了直播公开课，才知道createGameScene这个方法是开始游戏场景。

　　　　这不。。。。。。我笔记又断了。

　　　　甚至到了后面更加严重，连EUI界面都显示不出来。

　　　　这是书中内容：

　　　　　　1、创建EUI界面的EXML文件，起名为MainSkin.exml。（书中并没有提到在哪个目录下创建该文件。）

　　　　　　　　　

　　　　　　　　　

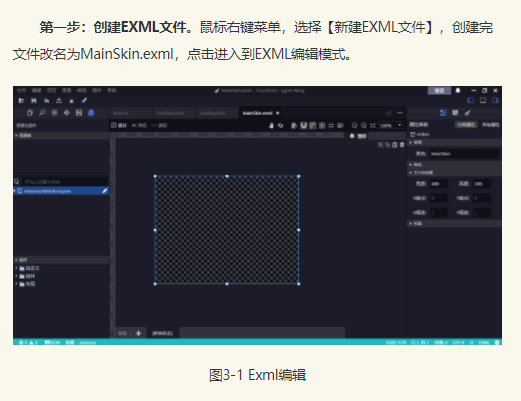
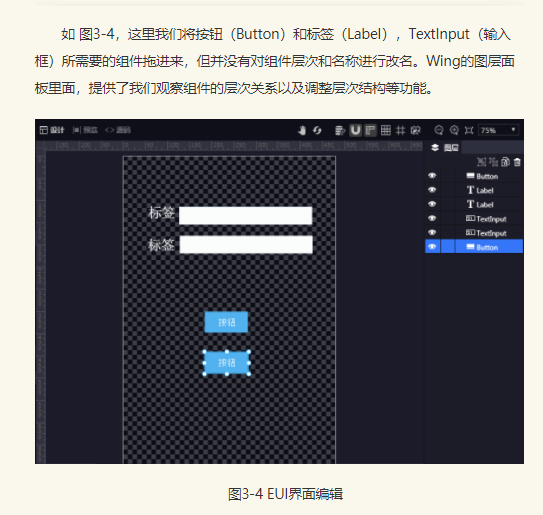
　　　　　　　　2、创建绑定类ts文件，起名为MainView.ts，注意设置关联MainSkin.exml文件的皮肤名字（我在截图中才发现MainSkin.exml原来是在src目录下）

　　　　　　　　　　　

　　　　　　　　　　

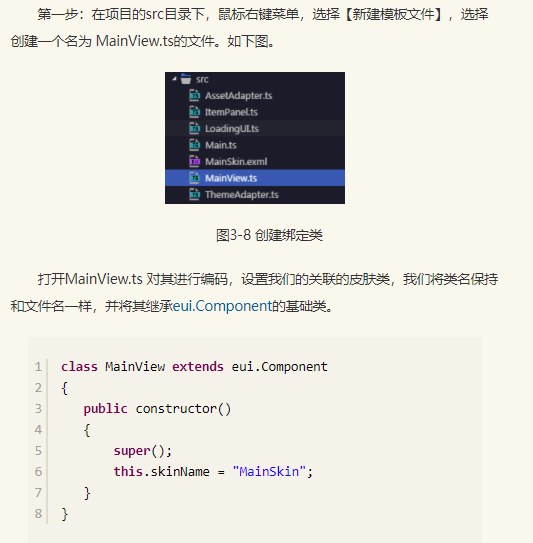
　　　　　　　　3、实例化界面（startCreateScene这个方法已经淘汰了，现在是用的createGameScene，在上文我有提到）

　　　　　　　　　　

　　　　好，接下来这是我的操作：

　　　　　　1、创建EUI界面的EXML文件，起名为MainSkin.exml，包括源码里的皮肤名称也注意了。

　　　　　　　　

　　　　　　　　

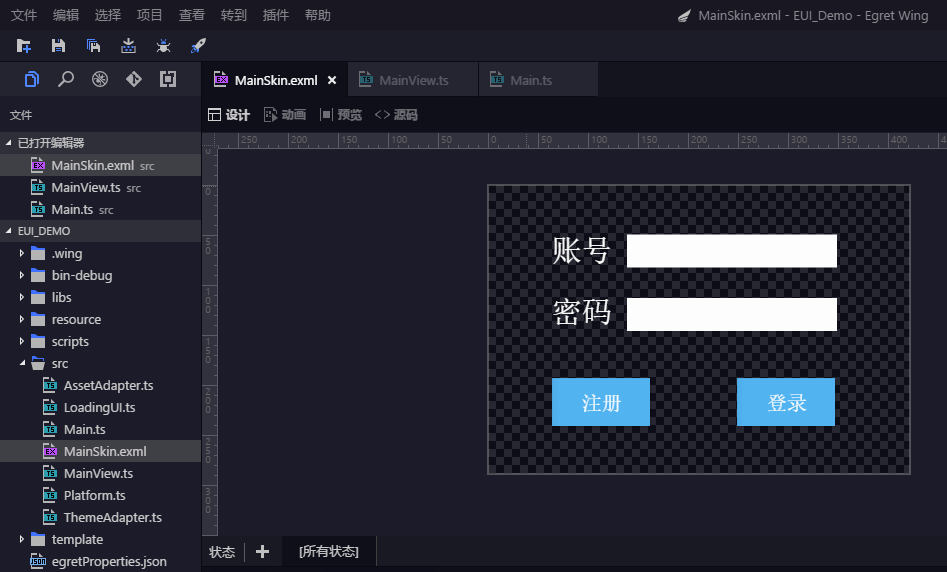
　　　　　　2、创建绑定类ts文件，起名为MainView.ts，注意设置关联MainSkin.exml文件的皮肤名字。

　　　　　　　　

　　　　　　3、实例化界面

　　　　　　　　

　　　　　　4、运行效果

　　　　　　　　

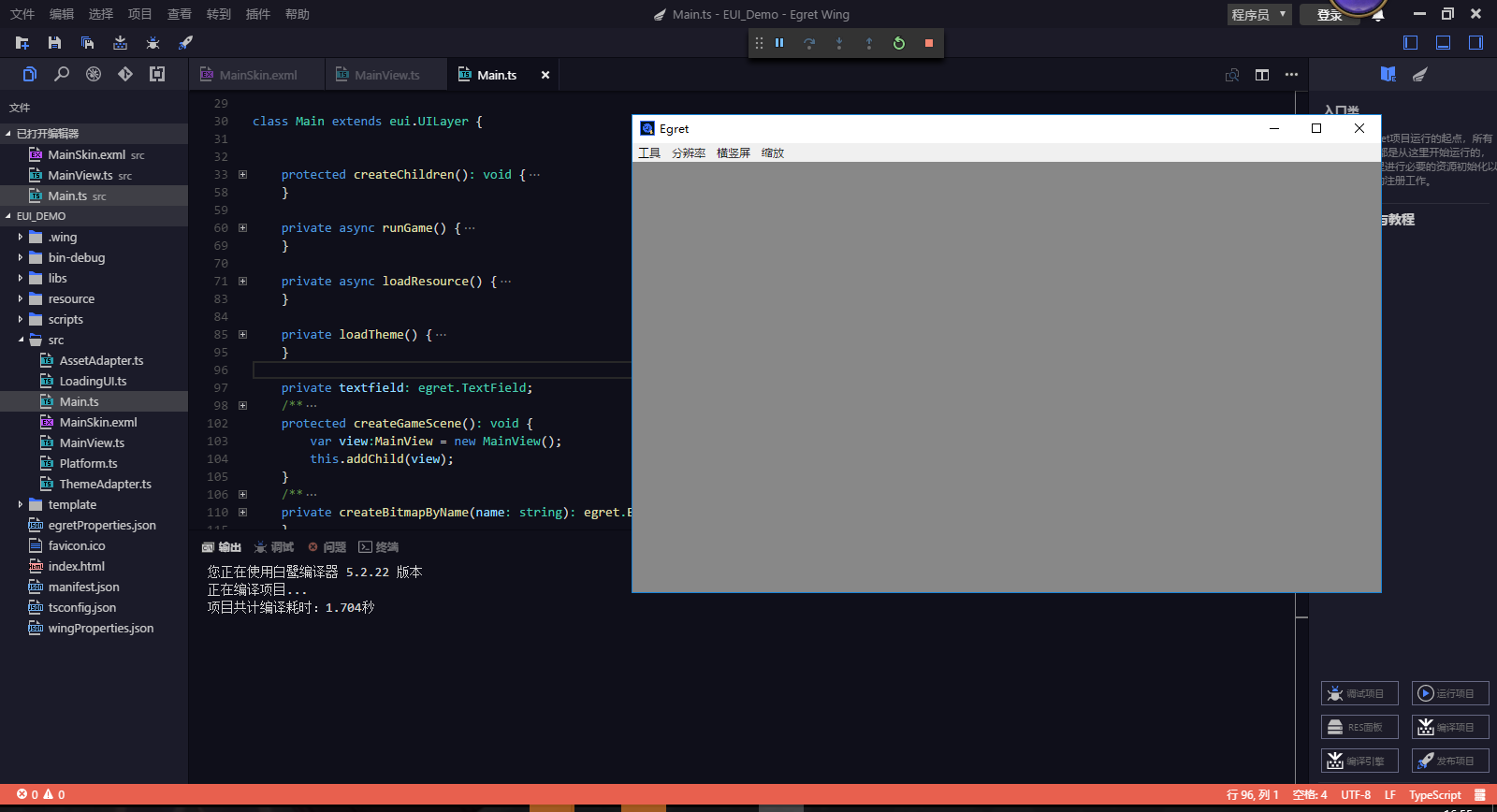
　　　　　　　你怕不是在逗我吧，老哥？嘛效果都木有！

　　　　我找群里的人问也没几个人回我，回我的，要么和我吹牛，要么叫我去看白鹭官方文档，好吧我去瞅瞅：

　　　　　　

　　　　一脸懵逼。。。。。。这对于小白的我简直就是。。。。。。不说了。

　　　　迷茫的我，又再次找上了度娘，2019年该如何入门Egret？这不，看到了一篇博客：

　　　　　　https://www.cnblogs.com/cloud-/p/10453496.html

　　　　　　这篇博客的发布时间是 2019-02-28 22:10 ，但是这篇博客推荐我去看这本书。

　　　　　　　

　　　　　　点击链接后，跳转：

　　　　　　

　　　　　　。。。。。。

　　　　　　

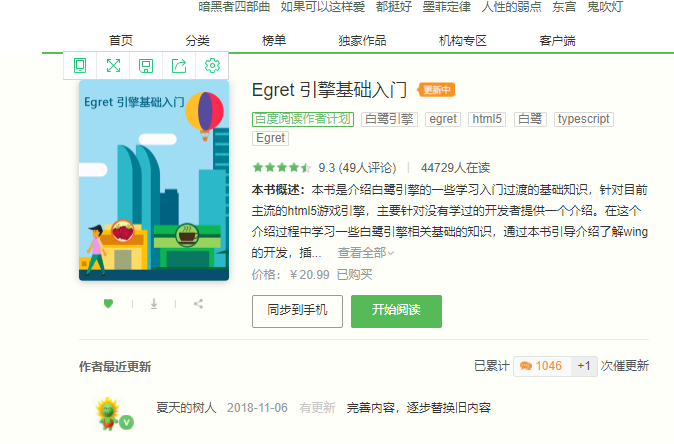
　　　　　　我看还不行么。。。。。。

　　　　　　

　　

　 （

　　　　来自 2019-7-23 的我：

　　　　　　书中目录：

　　　　　　

　　　　　　

　　　　　   

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　　　　　

　　）