点云ICP注册

背景

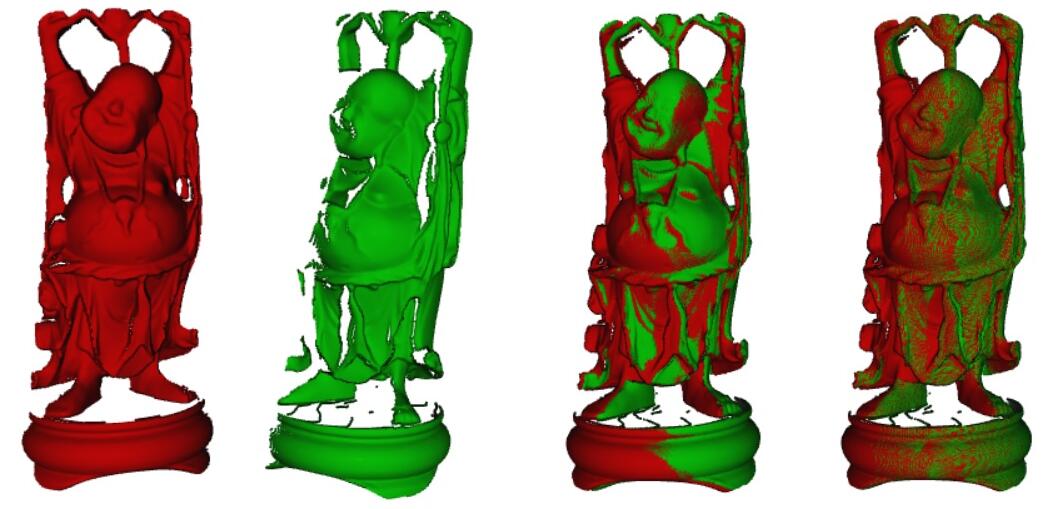
两个点云要注册在一块，一般分两个步骤：先做一个大致的对齐，也就是所谓的初始注册，一般可以通过一些可靠的点对来计算得到（如图3所示）；然后在初始注册的基础上进行精细注册，提升注册的精度（如图4所示）。精细注册的方法，一般采用ICP算法，也就是最近点迭代的方法。

ICP算法总览

下面先总的介绍一下ICP算法，之后再详细介绍里面的一些重要步骤。

算法输入是两片有部分重叠的点云a和b，并且已经初始注册好了，输出是ICP注册的刚体变换T：

1. 对b进行点采样，得到采样点集s

2. 在a中寻找采样点集s的最近对应点，得到点对集合c

3. 对c中的点云进行加权处理，并删掉一些不好的点对

4. 应用目标能量来优化点对距离，得到刚体变换Ti。Ti对采样点集进行刚体变换

5. 迭代步骤2-4，直到目标能量优化停止。T=Tn * ...... T1 * T0

点采样

由于计算速度的要求，一般是需要对点云b进行采样。然后用采样点去找对应进行优化。除了计算上的要求，如果用全点云进行匹配的话，精度也不会更加的好。因为更好的采样方法可以避免陷入能量局部极小的情况。常见的采样方法有均匀采样和几何采样。

均匀采样：采样点分布均匀，采样速度快，适合几何特征比较多的点云。因为这样的点云，均匀采样总能采样到几何特征。如果几何特征少的话，如下左图所示，有可能就采样不到几何特征。
几何采样：采样点会在几何特征明显的地方被采样到，如下右图所示。它能够抓住点云的几何特征，使得注册精度更高，更稳定。计算速度可能会慢一些，并且不太适合噪音比较大的点云，因为噪音其实就是几何特征了。

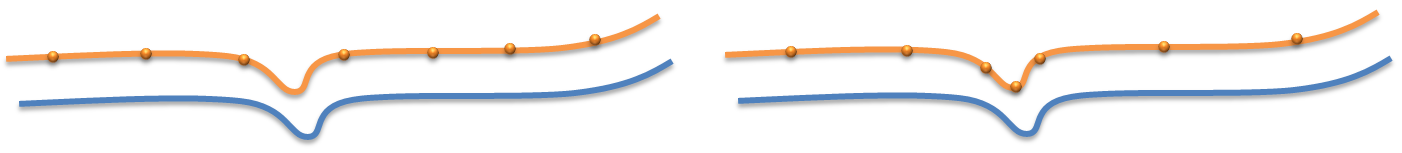
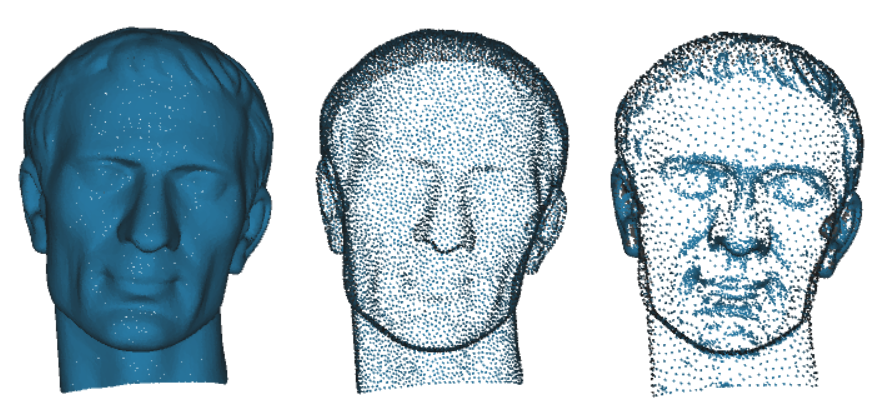
一个比较理想的采样方法，既能够采样到点云的几何特征，分布上也能做到局部均匀，然后就是计算速度要快。下面是一个采样示例，左图是原始点云，中间图是均匀采样，右图是几何采样。

点对应

从ICP的名字，就能看出点对应怎么去找，也就是给每个采样点找最近点。查找最近点是比较简单的，一般用KD Tree来加速查找。这些点对，有些是无效的，需要剔除掉。常用的剔除策略有距离和法线：

距离：点云a和b一般只有部分重叠，b的采样点集里，有部分点在a里是没有对应的。记这部分点为c，那么c的对应点对是需要剔除掉的。经过观察，我们发现c的点对距离一般是比较大的，所以可以设置一个距离阈值，来过滤掉这些点对。这个阈值算是一个参数了，可以根据点云的平均距离来设置，迭代开始的时候设置的大一些，如果找到的点对数目太少，可以适当的增大这个距离阈值。ICP迭代过程中，点云距离会逐渐减小，这个距离阈值也可以随之动态减小。
法线：在ICP迭代初期，点云位姿相差比较大，很多距离相近的点对也是错误的无效点对。我们可以根据点的一些属性来过滤掉这些无效的点对。常用的属性就是点云法线。比如点法线夹角要小于一个角度阈值。这个阈值和距离阈值一样，也是动态变换的。

目标能量

常用的目标能量有两种：点到点的能量和点到平面的能量。直观上讲，点到点的能量如左图所示，优化的是有效点对之间的距离；点到平面的能量，如右图所示，优化的是点到点云局部平面的距离。

点到点的能量：∑ || a - T(s) ||：其中s是点云b的有效采样点，a是s对应的点，T是刚体变换
点到平面的能量：∑ || (a - T(s)) * n(s) ||：其中n(s)是采样点s的法线

这两个能量，各有优缺点：

速度：本质上两个能量都是优化两个点云曲面的距离，点到点能量是线性收敛，点到平面能量的迭代等价于Gauss-Newton迭代，它的收敛速度是优于线性收敛的，情况好的时候，可以达到二阶收敛速度。
点到点能量不需要法线信息。有时候可靠的法线信息不容易得到，比如曲面严重不光滑，噪音十分严重，或者点云相对于物体采样非常稀疏等。不可靠的法线会使得点到平面的能量优化不稳定。

求解目标能量

能量里面只有T的旋转变换是非线性的，可以转化成线性最小二乘求解。常用的两种转化方式：

一种是把T当作仿射变换，对求解得到的T做SVD分解，求得仿射变换在刚体变换空间中的投影
另一种是把旋转矩阵用欧拉角的方式来表示，这样T里面的非线性部分就是sin和cos。我们假设每次迭代刚体变换的旋转角度不大，则cos(theta) = 1, sin(theta) = theta。这样就把T转化为线性矩阵了。

迭代停止条件

迭代算法总要有个停止条件。这个看似平凡的步骤，却是所有迭代算法的关键。它能影响算法最终的效果和性能。ICP常见的迭代停止条件：

最大迭代次数
迭代过程中，刚体变换近似恒等变换了
迭代过程中，点云之间的距离小于一定的阈值
迭代过程中，点云之间的距离越来越大了，需要中止无效迭代。或者更新算法参数重新迭代。

有兴趣的读者，欢迎参考视频版本