最长上升子序列（N*log（N））hdu1025

（HDU1025）

Constructing Roads In JGShining's Kingdom

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 18804    Accepted Submission(s): 5311

Problem Description

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.

Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource. You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource.

With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.

Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II.

The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones.

But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.

For example, the roads in Figure I are forbidden.

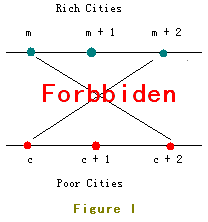
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

 

Input

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.

 

Output

For each test case, output the result in the form of sample. 
You should tell JGShining what's the maximal number of road(s) can be built. 

 

Sample Input

2

1 2

2 1

3

1 2

2 3

3 1

 

Sample Output

Case 1: My king, at most 1 road can be built. Case 2: My king, at most 2 roads can be built.

 题意：上面n个点，下面n个点，然后在这2n个点之间随意连线，一个点只能被连一次，问最多有多少条线不交叉。

方法一：upper_bound()容器

 #include"stdio.h"
 #include"string.h"
 #include"stdlib.h"
 #include"algorithm"
 #include"queue"
 #include"math.h"
 #include"iostream"
 #include"vector"
 #define M 100009
 #define inf 0x3f3f3f3f
 #define eps 1e-9
 #define PI acos(-1.0)
 #include"map"
 #include"vector"
 #include"set"
 #include"string"
 #include"stack"
 #define LL __int64
 using namespace std;
 int a[M],b[M],n;
 int finde()
 {
     int t=;
     b[t]=a[];
     t++;
     for(int i=;i<=n;i++)
     {
         int id=upper_bound(b,b+t,a[i])-b;
         //在b数组中弹出比ai大的最左边的元素，然后返回下标，否则返回last的下标
         if(id==t)
             t++;
         b[id]=a[i];
     }
     return t;
 }
 int main()
 {
     int kk=;
     while(scanf("%d",&n)!=-)
     {

         for(int i=;i<=n;i++)
         {
             int k,p;
             scanf("%d%d",&k,&p);
             a[k]=p;
         }
         int leng=finde();
         printf("Case %d:\n",kk++);
         if(leng==)
             cout<<"My king, at most "<< leng <<" road can be built."<<endl;
         else
             cout<<"My king, at most "<< leng <<" roads can be built."<<endl;
         cout<<endl;
     }
     return ;
 }

方法二：二分查找

 #include"stdio.h"
 #include"string.h"
 #include"stdlib.h"
 #include"algorithm"
 #include"queue"
 #include"math.h"
 #include"iostream"
 #include"vector"
 #define M 100009
 #define inf 0x3f3f3f3f
 #define eps 1e-9
 #define PI acos(-1.0)
 #include"map"
 #include"vector"
 #include"set"
 #include"string"
 #include"stack"
 #define LL __int64
 using namespace std;
 int a[M],b[M],c[M],n;
 int finde(int n,int k)
 {
     int l=;
     int r=n;
     while(l<=r)
     {
         int mid=(l+r)/;
         if(c[mid]<k)
             l=mid+;
         else
             r=mid-;
     }
     return l;
 }
 int main()
 {
     int kk=;
     while(scanf("%d",&n)!=-)
     {

         for(int i=;i<=n;i++)
         {
             int k,p;
             scanf("%d%d",&k,&p);
             a[k]=p;
         }
         memset(c,inf,sizeof(c));
         b[]=;
         c[]=a[];
         for(int i=;i<=n;i++)
         {
             int id=finde(n,a[i]);
             c[id]=a[i];
             b[i]=id;
         }
         int leng=;
         for(int i=;i<=n;i++)
             leng=max(leng,b[i]);

         printf("Case %d:\n",kk++);
         if(leng==)
             cout<<"My king, at most "<< leng <<" road can be built."<<endl;
         else
             cout<<"My king, at most "<< leng <<" roads can be built."<<endl;
         cout<<endl;
     }
     return ;
 }

 方法三：模拟upper_bound

 #include"stdio.h"
 #include"string.h"
 #include"stdlib.h"
 #include"algorithm"
 #include"queue"
 #include"math.h"
 #include"iostream"
 #include"vector"
 #define M 100009
 #define inf 0x3f3f3f3f
 #define eps 1e-9
 #define PI acos(-1.0)
 #include"map"
 #include"vector"
 #include"set"
 #include"string"
 #include"stack"
 #define LL __int64
 using namespace std;
 int a[M],b[M],c[M],n;
 int binary_find(int n,int k)
 {
     int l=;
     int r=n-;
     while(l<=r)
     {
         int mid=(l+r)/;
         if(b[mid]>=k)
             r=mid-;
         else
             l=mid+;
     }
     return l;
 }
 int fun(int n)
 {
     int t=;
     b[t]=a[];
     t++;
     for(int i=;i<=n;i++)
     {
         int id=binary_find(t,a[i]);
         if(id==t)
             t++;
         b[id]=a[i];
     }
     return t;
 }
 int main()
 {
     int kk=;
     while(scanf("%d",&n)!=-)
     {

         for(int i=;i<=n;i++)
         {
             int k,p;
             scanf("%d%d",&k,&p);
             a[k]=p;
         }
         int leng=fun(n);
         printf("Case %d:\n",kk++);
         if(leng==)
             cout<<"My king, at most "<< leng <<" road can be built."<<endl;
         else
             cout<<"My king, at most "<< leng <<" roads can be built."<<endl;
         cout<<endl;
     }
     return ;
 }