建模算法(一)——线性规划
一、解决问题
主要是安排现有资源(一定),取得最好的效益的问题解决,而且约束条件都是线性的。
二、数学模型
1、一般数学模型
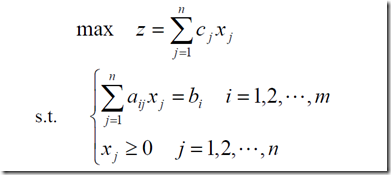
2、MATLAB数学模型
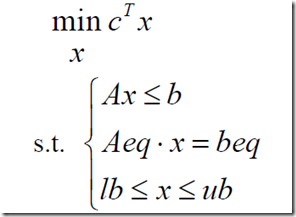
其中c,x都是列向量,A,Aeq是一个合适的矩阵,b,beq是合适的列向量。然后lb和ub是下限和上线(但是请注意= =,lb是一个变量的名字)
三、相关方程解法
1、图解法,画出可行域,这个可以进行编程进行实现、
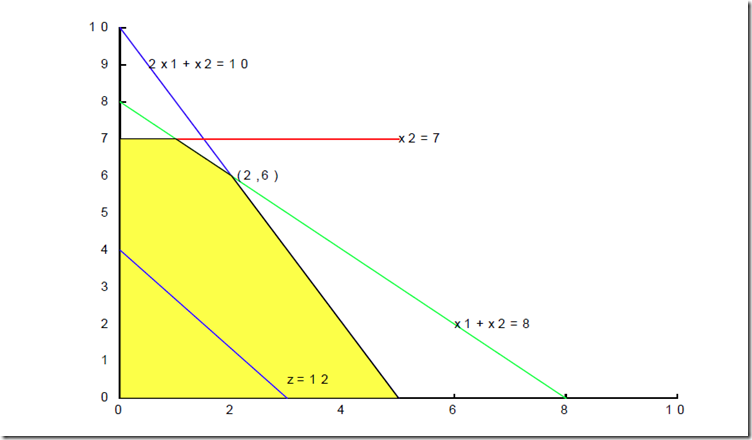
2、直接使用MATLAB的相关方法进行解题、
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,Xo,OPTIONS)
其中fval返回的是目标函数的值,然后x则是返回取到fval时x的对应的值,然后LB和UB是对应x的上界和下界(可以省略),x0是x的初始值(暂时可以忽略)
OPTIONS是控制参数。
四、一些其他问题转换成线性规划
1、绝对值之和最小
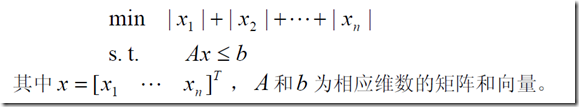
在这里我们就可以令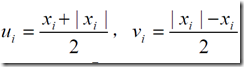 ,就可以满足
,就可以满足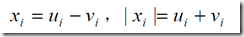 ,这样子这个问题就变成了
,这样子这个问题就变成了

2、两个数的差的绝对值,在xi固定时,取得max,之后在去定yi
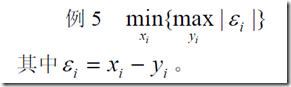
我们取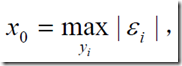 ,就可以转换问题了
,就可以转换问题了
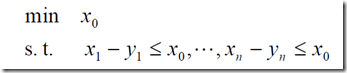
五、一些线性规划可以解决的实际问题
1、生产力有限,要求取得最大收益

2、运输问题(产销问题)
要求运输费用最小

在这里需要记得有一个很重要的等式,就是所有产地送出去的等于所有销售地收到的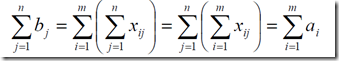
3、指派问题
要求花费的工作时间要最短

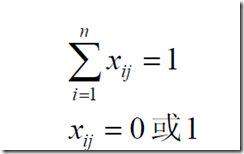
(2)求解指派问题的匈牙利算法、
首先我们要知道对与系数矩阵C由这样的性质,同时对每一行(列)加上或者减去同样的一个数,得到的新矩阵和原矩阵的指派问题具有相同的最优指派。
一般步骤是:
a、每行每列消除最小的数字,使得出现能够出现N(与矩阵大小相同)个位于不同行不同列的零元素,选定就是最优解。
b、如果上一步骤没办法直接完成,则、

4、对偶理论(与反函数相比较)
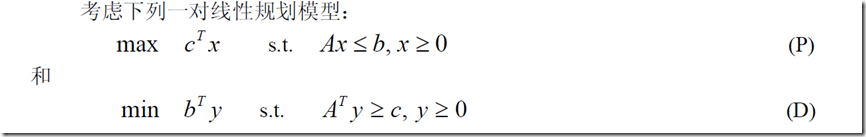

最重要的是掌握其性质,可以用来检验是不是最优解、、

5、投资的收益和风险(主要多目标函数如何并成一个目标函数)

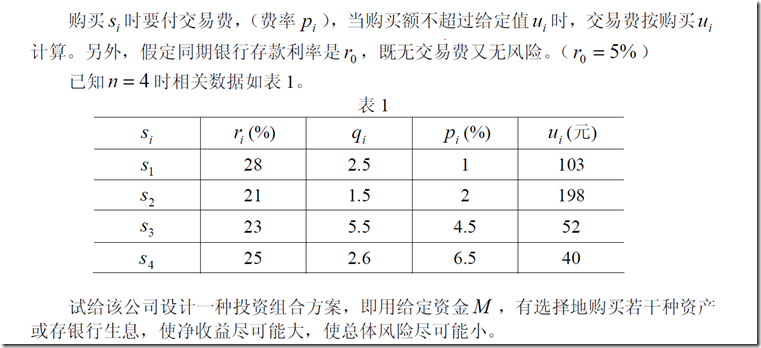
下一步主要是设立变量(这是数学建模中一步很关键的地方,你指标选的好,方程就好列好解,否则。。。。)

之后就是加入限定,一些理想化的假设

然后写出方程

其中第一个目标函数为收益,第二个为风险。
下一步就是化简目标函数
(1)固定风险水平,优化收益

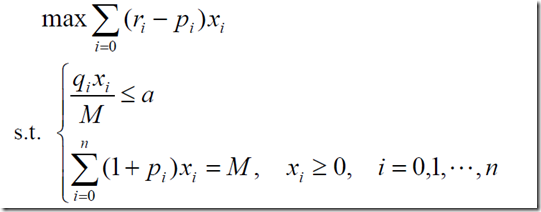
(2)固定盈利水平,极小化风险

(3)同时考虑两个,这样的话需要加入一个权重s。
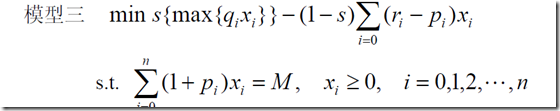
建模算法(一)——线性规划的更多相关文章
- Python小白的数学建模课-03.线性规划
线性规划是很多数模培训讲的第一个算法,算法很简单,思想很深刻. 要通过线性规划问题,理解如何学习数学建模.如何选择编程算法. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛 ...
- 建模算法(三)——非线性规划
一.非线性规划和线性规划不同之处 1.含有非线性的目标函数或者约束条件 2.如果最优解存在,线性规划只能存在可行域的边界上找到(一般还是在顶点处),而非线性规划的最优解可能存在于可行域的任意一点达到. ...
- 建模算法(二)——整数规划
一.概述 1.定义:规划中变量部分或全部定义成整数是,称为整数规划. 2.分类:纯整数规划和混合整数规划. 3.特点: (1)原线性规划有最优解,当自变量限制为整数后: a.原最优解全是整数,那最优解 ...
- python 版 mldivide matlab 反除(左除)《数学建模算法与程序》Python笔记
今天在阅读数学建模的时候看到了差分那章 其中有一个用matlab求线性的代码,这里我贴出来 这里我送上 Python代码 In [39]: import numpy as np ...: from s ...
- 建模算法(十一)——目标规划
求解多目标规划的思路 1.加权系数法 为每一个目标加一个权系数,把多目标模型转化成单一目标模型.但是困难时确定合理的权系数,以反映不同目标之间的重要程度. 2.优先等级法 将各目标按其重要程度分为不同 ...
- 建模算法(十)——灰色理论之关联度分析
一.数据变换技术 为了保证建模的质量和系统分析结果的准确性,对原始的数据要进行去量纲处理. 1.定义 设有序列,则成映射为序列x到序列y的数据变换. (1) f 是初值化变换. (2) f 是均值化变 ...
- 建模算法(六)——神经网络模型
(一)神经网络简介 主要是利用计算机的计算能力,对大量的样本进行拟合,最终得到一个我们想要的结果,结果通过0-1编码,这样就OK啦 (二)人工神经网络模型 一.基本单元的三个基本要素 1.一组连接(输 ...
- 建模算法(五)——图与网络
(一)图与网络的基本概念 一.无向图 含有的元素为顶点,弧和权重,但是没有方向 二.有向图 含有的元素为顶点,弧和权重,弧具有方向. 三.有限图.无限图 顶点和边有限就是有限图,否则就是无限图. 四. ...
- 【BZOJ1937】[Shoi2004]Mst 最小生成树 KM算法(线性规划)
[BZOJ1937][Shoi2004]Mst 最小生成树 Description Input 第一行为N.M,其中 表示顶点的数目, 表示边的数目.顶点的编号为1.2.3.…….N-1.N.接下来的 ...
随机推荐
- C# Socket大文件上传
public sealed class SocketData { private SocketData() { } public static SendFileMode SendFile(Socket ...
- DetachedCriteria详细使用
一.基本使用 1. 说明 Restrictions 是产生查询条件的工具类. 2. 定义 可以直接用class 创建 DetachedCriteria searDc = DetachedCriteri ...
- MongoDB的快速手动安装
上一篇文章<MongoDB.WebIDE:升级版的Mongodb管理工具>漏了点东西:就是关于MongoDB主从库的安装配置和启动.网上关于MongoDB的安装有大量的文章供大家学习.我这 ...
- 我用的/etc/vimrc
" 映射非数字/字母键, 如:ctrl,shift, alt, home,end,功能键F1~F12, 要把这些键用尖括号括起来!如: map <F3> :NERDTree< ...
- 安装lnmp后,忘记phpmyadmin的root密码,怎么办
如果忘记MySQL root密码,如何重设密码?执行如下命令:wget http://soft.vpser.net/lnmp/ext/reset_mysql_root_password.sh;sh r ...
- 简论:int i = 0
int i =0; 或许这就是i和0的缘分吧...
- 想在BD自然排名中脱颖而出吗?加张合适的图片吧!
经常在BD或gg搜索不难发现有些搜索结果会带有缩略图,类似下图,图文搭配,看着不累 在一大排搜索结果中,都是文字的话,还没认真看就感觉累,如果在这些搜索结果中突然出现一条图文结合的条目,是不是有耳目一 ...
- php面试题之五——PHP综合应用(高级部分)
五.PHP综合应用 1.写出下列服务的用途和默认端口(新浪网技术部) ftp.ssh.http.telnet.https ftp:File Transfer Protocol,文件传输协议,是应用层的 ...
- 淘宝(阿里百川)手机客户端开发日记第三篇 SlidingPaneLayout实现侧滑菜单
需要的三个布局文件: activity_main.xml :主窗体布局 left.xml : 左侧栏目分类布局 right.xml : 右侧内容详情 需要的组件: android.support.v4 ...
- Python strip、lstrip和rstrip的用法
Python中strip用于去除字符串的首尾字符,同理,lstrip用于去除左边的字符,rstrip用于去除右边的字符. 这三个参数都可以传入一个参数,指定要去除的首尾字符. 需要注意的是,传入的是一 ...
