用MATLAB对信号做频谱分析

1.首先学习下傅里叶变换的东西。学高数的时候老师只是将傅里叶变换简单的说了下，并没有深入的讲解。而现在看来，傅里叶变换似乎是信号处理的方面的重点只是呢，现在就先学习学习傅里叶变换吧。

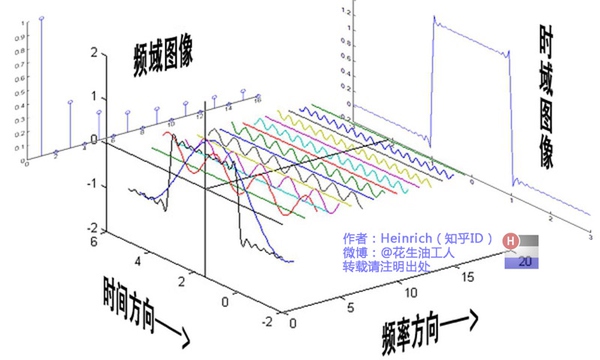
上面这幅图在知乎一个很著名的关于傅里叶变换的文章中的核心插图，我觉得这幅图很直观的就说明了傅里叶变换的实质。时域上的东西直观的反应到了频域上了，很完美的结合到了一起，233333.  无数正弦波叠加，震荡的叠加的最后结果竟然是方波，同理，任何周期性函数竟然都能拆分为傅里叶级数的形式，这样的简介与优雅，真令人折服。

2.MATLAB对信号做频谱分析

代码：(1)对 f1 = Sa(2t)的频谱分析

 clear;clc;
 hold on;
 R=0.05;
 t=-1.2:R:1.2;
 t1 = *t;
 f1=sinc(t1);                       %Sa函数
 subplot(,,),plot(t,f1)
 xlabel('t'),ylabel('f1')
 axis([-,,-0.3,1.2]);             %写出Sa函数上下限

 N=;
 k=-N:N;
 W1=;
 W=k*W1/N;
 F=f1*exp(-j*t'*W)*R;               %f1的傅里叶变换
 F=real(F);                         %取F的实部
 subplot(,,),plot(W,F)
 xlabel('W'),ylabel('F(jw)')  

结果如下图：

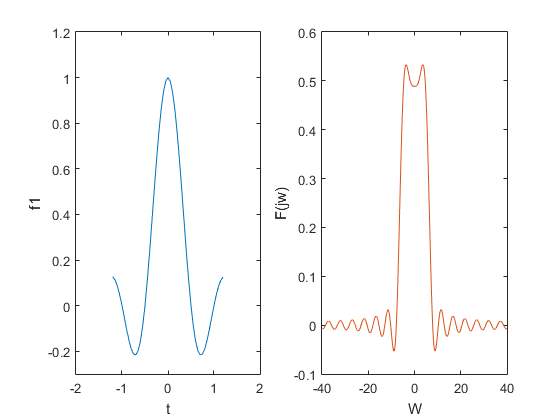
(2)对 f2 = u(t+2) - u(t-2)的频谱分析

 R=0.05;
 t=-:R:;
 f2=(t>=-)-(t>=);
 subplot(,,),plot(t,f2)
 grid on;
 xlabel('t'),ylabel('f2')
 axis([-,,-0.5,1.5]);

 N=;k=-N:N;
 W1=;
 W=k*W1/N;
 F=f2*exp(-j*t'*W)*R;
 F=real(F);
 subplot(,,),plot(W,F)
 grid on;
 xlabel('W'),ylabel('F(jw)')  

结果如下图：

(3)对f3 = t[u(t+1) - u(t-1) ]的频谱分析

 R=0.05;
 h=0.001;
 t=-1.2:R:1.2;
 y=t.*(t>=-)-t.*(t>=);
 f4=diff(y)/h;
 subplot(,,),plot(t,y)
 xlabel('t'),ylabel('y')
 axis([-1.2,1.2,-1.2,1.2]);

 N=;
 k=-N:N;
 W1=;
 W=k*W1/N;
 F=y*exp(-j*t'*W)*R;
 F=real(F);
 subplot(,,),plot(W,F)
 xlabel('W'),ylabel('F(jw)')
 axis([-,,-0.06,0.06]);

结果如下图：

(4)对正弦波做FFT频谱分析

 %*************************************************************************%
 %                              FFT实践及频谱分析                           %
 %*************************************************************************%
 %***************正弦波****************%
 fs=;%设定采样频率
 N=;
 n=:N-;
 t=n/fs;
 f0=;%设定正弦信号频率
 %生成正弦信号
 x=sin(*pi*f0*t);
 figure();
 subplot();
 plot(t,x);%作正弦信号的时域波形
 xlabel('t');
 ylabel('y');
 title('正弦信号y=2*pi*10t时域波形');
 grid; 

 %进行FFT变换并做频谱图
 y=fft(x,N);%进行fft变换
 mag=abs(y);%求幅值
 f=(:length(y)-)'*fs/length(y);%进行对应的频率转换
 figure();
 subplot();
 plot(f,mag);%做频谱图
 axis([,,,]);
 xlabel('频率(Hz)');
 ylabel('幅值');
 title('正弦信号y=2*pi*10t幅频谱图N=128');
 grid; 

 %求均方根谱
 sq=abs(y);
 figure();
 subplot();
 plot(f,sq);
 xlabel('频率(Hz)');
 ylabel('均方根谱');
 title('正弦信号y=2*pi*10t均方根谱');
 grid; 

 %求功率谱
 power=sq.^;
 figure();
 subplot();
 plot(f,power);
 xlabel('频率(Hz)');
 ylabel('功率谱');
 title('正弦信号y=2*pi*10t功率谱');
 grid; 

 %求对数谱
 ln=log(sq);
 figure();
 subplot();
 plot(f,ln);
 xlabel('频率(Hz)');
 ylabel('对数谱');
 title('正弦信号y=2*pi*10t对数谱');
 grid; 

 %用IFFT恢复原始信号
 xifft=ifft(y);
 magx=real(xifft);
 ti=[:length(xifft)-]/fs;
 figure();
 subplot();
 plot(ti,magx);
 xlabel('t');
 ylabel('y');
 title('通过IFFT转换的正弦信号波形');
 grid; 

执行结果如下图：

(5)对矩形波做FFT频谱分析

 %****************.矩形波****************%
 fs=;%设定采样频率
 t=-:0.1:;
 x=rectpuls(t,);
 x=x(:);
 figure();
 subplot(); plot(t(:),x);%作矩形波的时域波形
 xlabel('t');
 ylabel('y');
 title('矩形波时域波形');
 grid; 

 %进行FFT变换并做频谱图
 y=fft(x);%进行fft变换
 mag=abs(y);%求幅值
 f=(:length(y)-)'*fs/length(y);%进行对应的频率转换
 figure();
 subplot();
 plot(f,mag);%做频谱图
 xlabel('频率(Hz)');
 ylabel('幅值');
 title('矩形波幅频谱图');
 grid; 

 %求均方根谱
 sq=abs(y);
 figure();
 subplot();
 plot(f,sq);
 xlabel('频率(Hz)');
 ylabel('均方根谱');
 title('矩形波均方根谱');
 grid; 

 %求功率谱
 power=sq.^;
 figure();
 subplot();
 plot(f,power);
 xlabel('频率(Hz)');
 ylabel('功率谱');
 title('矩形波功率谱');
 grid; 

 %求对数谱
 ln=log(sq);
 figure();
 subplot();
 plot(f,ln);
 xlabel('频率(Hz)');
 ylabel('对数谱');
 title('矩形波对数谱');
 grid; 

 %用IFFT恢复原始信号
 xifft=ifft(y);
 magx=real(xifft);
 ti=[:length(xifft)-]/fs;
 figure();
 subplot();
 plot(ti,magx);
 xlabel('t');
 ylabel('y');
 title('通过IFFT转换的矩形波波形');
 grid; 

执行结果如下图：

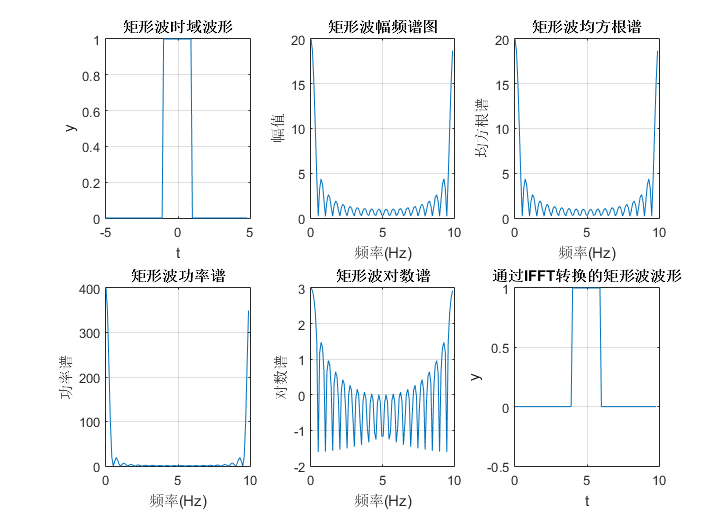
(6)对白噪声做频谱分析

 %****************.白噪声****************%
 fs=;%设定采样频率
 t=-:0.1:;
 x=zeros(,);
 x()=;
 figure();
 subplot();
 plot(t(:),x);%作白噪声的时域波形
 xlabel('t');
 ylabel('y');
 title('白噪声时域波形');
 grid; 

 %进行FFT变换并做频谱图
 y=fft(x);  %进行fft变换
 mag=abs(y);%求幅值
 f=(:length(y)-)'*fs/length(y);%进行对应的频率转换
 figure();
 subplot();
 plot(f,mag);%做频谱图
 xlabel('频率(Hz)');
 ylabel('幅值');
 title('白噪声幅频谱图');
 grid; 

 %求均方根谱
 sq=abs(y);
 figure();
 subplot();
 plot(f,sq);
 xlabel('频率(Hz)');
 ylabel('均方根谱');
 title('白噪声均方根谱');
 grid; 

 %求功率谱
 power=sq.^;
 figure();
 subplot();
 plot(f,power);
 xlabel('频率(Hz)');
 ylabel('功率谱');
 title('白噪声功率谱');
 grid; 

 %求对数谱
 ln=log(sq);
 figure();
 subplot();
 plot(f,ln);
 xlabel('频率(Hz)');
 ylabel('对数谱');
 title('白噪声对数谱');
 grid; 

 %用IFFT恢复原始信号
 xifft=ifft(y);
 magx=real(xifft);
 ti=[:length(xifft)-]/fs;
 figure();
 subplot();
 plot(ti,magx);
 xlabel('t');
 ylabel('y');
 title('通过IFFT转换的白噪声波形');
 grid;   

执行结果如下：