MH/T4029.3 IFPL报文解析

MH/T4029.3是民航业用来规定飞行计划相关数据交互的规范,今天我们先来解析下其中I类的IFPL报文.

我们先来看看IFPL报文长啥样.

ZCZC

-TITLE IFPL

-FILTIM 010909

-IFPLID 201332005

-SOURCE AIRNET:ZUCK

-ARCID CSN6435

-ADEP ZBAA

-ADES ZUUU

-EOBD 20130301

-EOBT 0850

-SSRCODE A1270

NNNN

其中ZCZC是报文的开头标记,NNNN是报文的结束标记,没有实际意义

反序列化

1. 下面我们根据报文创建我们的对象,忽略报头和报尾

    class IFPL
    {
        public string TITLE { get; set; }
        public string FILTIM { get; set; }
        public string IFPLID { get; set; }
        public string SOURCE { get; set; }
        public string ARCID { get; set; }
        public string ADEP { get; set; }
        public string ADES { get; set; }
        public string EOBD { get; set; }
        public string EOBT { get; set; }
        public string SSRCODE { get; set; }
    }

1. 下面我们安装下MH/T4029.3报文解析工具,程序包控制台输入命令:
   
   Install-Package Extensioner.MHT40293 -Version 1.0.0
2. 反序列化报文

            var message = @"ZCZC
-TITLE IFPL
-FILTIM 010909
-IFPLID 201332005
-SOURCE AIRNET:ZUCK
-ARCID CSN6435
-ADEP ZBAA
-ADES ZUUU
-EOBD 20130301
-EOBT 0850
-SSRCODE A1270
NNNN";

            var model = MessageConvert.DeserializeObject<IFPL>(message);

            Console.ReadKey();

反序列化后的对象如下图:



是不是很简单?

序列化

反过来我们有时候需要把对象转换为MH/T4029.3报文,怎么办呢?也很简单!类库已经帮我们封装好了方法,我们直接调用即可.

我们把上面的model序列化然后打印一下

            var value = MessageConvert.SerializeObject(model);

            Console.WriteLine(value);

序列化后的报文入下图:



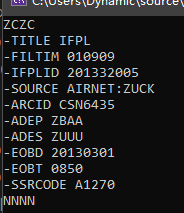
So easy!

完整代码如下:

点击查看代码

using Extensioner.MHT40293;
using System;

namespace MHT40293.IFPLTest
{
    class Program
    {
        static void Main(string[] args)
        {
            var message = @"ZCZC
-TITLE IFPL
-FILTIM 010909
-IFPLID 201332005
-SOURCE AIRNET:ZUCK
-ARCID CSN6435
-ADEP ZBAA
-ADES ZUUU
-EOBD 20130301
-EOBT 0850
-SSRCODE A1270
NNNN";

            var model = MessageConvert.DeserializeObject<IFPL>(message);

            var value = MessageConvert.SerializeObject(model);

            Console.WriteLine(value);

            Console.ReadKey();
        }
    }

    class IFPL
    {
        public string TITLE { get; set; }
        public string FILTIM { get; set; }
        public string IFPLID { get; set; }
        public string SOURCE { get; set; }
        public string ARCID { get; set; }
        public string ADEP { get; set; }
        public string ADES { get; set; }
        public string EOBD { get; set; }
        public string EOBT { get; set; }
        public string SSRCODE { get; set; }
    }

}