UVA12113-Overlapping Squares（二进制枚举）

Problem UVA12113-Overlapping Squares

Accept：116  Submit：596

Time Limit: 3000 mSec

 Problem Description

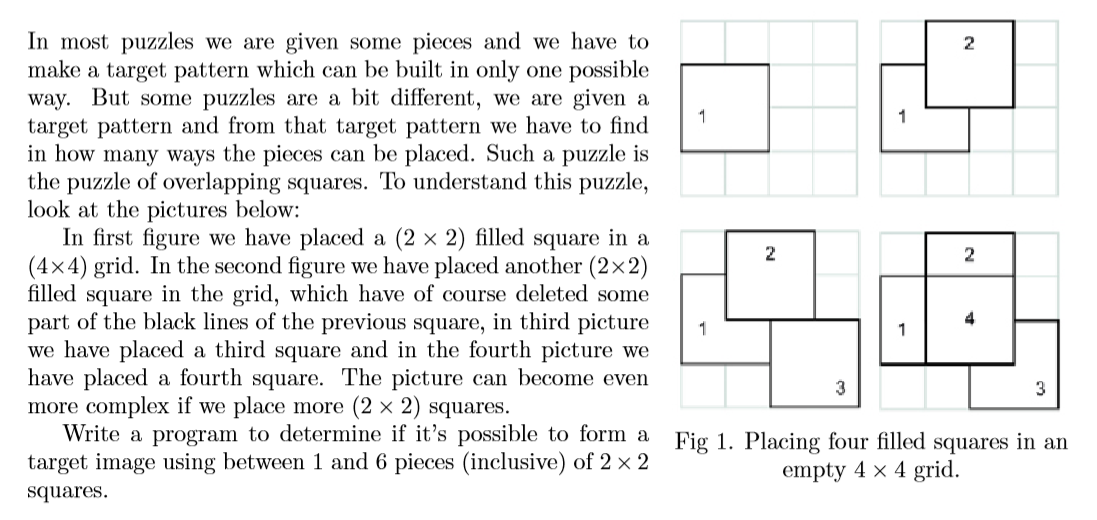
 Input

The input consists of several test cases. Each test case is contained in five lines and each line contains nine characters. If the horizontal border of a filled square is visible it is denoted with ‘ ’ (ASCII value 95) sign and if vertical border of a filled square is visible then it is denoted with ‘|’ (ASCII value 124) character. The board contains no other character than ‘ ’, ‘|’ and of course ‘ ’ (ASCII Value 32). The border lines of the squares can only be along the grid lines. Each board lines end with a ‘#’ (Hash character) which denotes the end of line. This character is not a part of the grid or square. The last test case is followed by a single zero, which should not be processed.

 Output

For each test case, print the case number and ‘Yes’ or ‘No’, depending on whether it’s possible to form the target.

 Sample Input

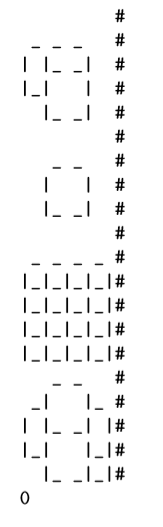
 Sample Ouput

Case 1: Yes
Case 2: Yes
Case 3: No
Case 4: Yes

题解：感觉最近做的题都十分考验代码能力（然而我很水），想到一共只有九种摆放方案之后这个题的思维就基本上结束了，所有的挑选方案只有2^9，直接二进制枚举，对于相同的挑选方案，不同的摆放顺序也会带来不同的覆盖结果，解决方法就是next_permutation()，预处理出来不同小正方形的覆盖格子的标号，接下来暴力就好。

 #include <bits/stdc++.h>

 using namespace std;

 const int maxn = (<<);
 const int N = ,M = ;
 const int kind = ;

 int edge[][] = {{,,,,,,,}};
 int core[][] = {{,,,}};
 int bits[kind+],target[N*M];

 int read(){
     char str[];
     int cnt = ,edges = ;
     for(int i = ;i < N;i++){
         gets(str);
         if(str[] == '') return -;
         for(int j = ;j < M;j++){
             if(str[j] == ' ') target[cnt++] = ;
             else target[cnt++] = ,edges++;
         }
     }
     return edges;
 }

 void init(){
     for(int i = ;i < ;i++){
         for(int j = ;j < ;j++){
             if(!i && !j) continue;
             int plus,minus;
             if(j == ) plus = ,minus = ;
             else plus = ,minus = ;
             for(int k = ;k < ;k++){
                 edge[i*+j][k] = edge[i*+j-minus][k]+plus;
             }
             for(int k = ;k < ;k++){
                 core[i*+j][k] = core[i*+j-minus][k]+plus;
             }
         }
     }
 }

 int bitcount(int s){
     return s ==  ?  : bitcount(s>>)+(s&);
 }

 void bitpos(int s){
     int cnt = ;
     for(int i = ;i < ;i++){
         if(s&(<<i)) bits[cnt++] = i;
     }
 }

 int iCase = ;

 int main()
 {
 #ifdef GEH
     freopen("helloworld.01,inp","r",stdin);
 #endif
     init();
     int edge_cnt;
     while(edge_cnt=read()){
         if(edge_cnt == -) break;
         int tmp[M*N];
         bool ok = false;
         for(int s = ;s < maxn;s++){
             int n = bitcount(s);
             bitpos(s);
             if(n> || n*<edge_cnt) continue;
             do{
                 memset(tmp,,sizeof(tmp));
                 for(int i = ;i < n;i++){
                     for(int j = ;j < ;j++){
                         tmp[edge[bits[i]][j]] = ;
                     }
                     for(int j = ;j < ;j++){
                         tmp[core[bits[i]][j]] = ;
                     }
                 }

                 if(memcmp(tmp,target,sizeof(target)) == ){
                     ok = true;
                     break;
                 }
             }while(next_permutation(bits,bits+n));
             if(ok) break;
         }
         printf("Case %d: ",iCase++);
         if(ok) printf("Yes\n");
         else printf("No\n");
     }
     return ;
 }