机器学习算法总结(二)——决策树（ID3, C4.5, CART）

　　决策树是既可以作为分类算法，又可以作为回归算法，而且在经常被用作为集成算法中的基学习器。决策树是一种很古老的算法，也是很好理解的一种算法，构建决策树的过程本质上是一个递归的过程，采用if-then的规则进行递归（可以理解为嵌套的 if - else 的条件判断过程），关于递归的终止条件有三种情形：

　　1）当前节点包含的样本属于同一类，则无需划分，该节点作为叶子节点，该节点输出的类别为样本的类别

　　2）该节点包含的样本集合为空，不能划分

　　3）当前属性集为空，则无法划分，该节点作为叶子节点，该节点的输出类别为样本中数量多数的类别

　　事实上，我们在递归的过程中不会等达到上面的条件才终止递归，往往会提前终止来减小过拟合（提前终止也是一种较好的减小过拟合的方式，不只是在决策树算法中，在很多场景下都有应用）。

　　决策树主要的有点是模型具有很好的可读性，模型可以可视化，分类速度快（log(n) 的时间复杂度），本文介绍三种最常见的决策树算法 — ID3，C4.5，CART，并介绍三种算法的优缺点。

1、信息论基础

　　首先我们需要熟悉信息论中熵的概念，熵度量了事物的不确定性，熵越大，表示事物的不确定性越高，混乱程度越高。则随机变量X的熵定义为：

　　

　　条件熵H(Y|X)表示在已经知道随机变量X的条件下随机变量Y的不确定性，随机变量X给定的条件下随机变量Y的条件熵H(Y|X)，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：

　　

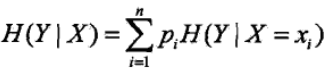
2、ID3算法

　　前面说过决策树本质上是 if-else 的嵌套，然而如何决定每一层的if 条件呢？在ID3算法中用的是信息增益作为选择特征的指标，信息增益的定义是在特征A给定的条件下，集合D的信息熵H(D) 和在 特征A条件下的条件熵H(D|A) 的差值，描述了选取特征A对数据集进行划分对信息熵的减小程度，信息增益的表达式：

　　

　　具体的信息增益计算过程如下：

　　1）计算数据集D的信息熵H(D)：

　　

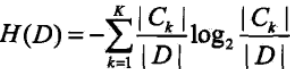
　　2）计算特征A对数据集D的条件熵H(D|A):

　　

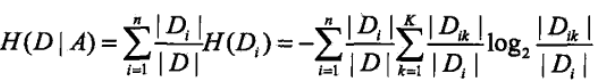
　　3）计算信息增益g(D, A)

　　

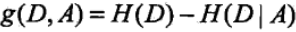
　　因此ID3算法的流程就很简单了，每次都采用信息增益来选取最优划分特征来划分数据集，直到遇到了递归终止条件，具体算法流程如下：

　　定义输入值：训练数据集D，特征集A（可以从训练集中提取出来），阀值ε（用来实现提前终止）；

　　1）若当前节点中所有实例属于同一类C_k，则该结点作为叶子节点，并将类别C_k作为该结点的输出类；

　　2）若A为空，则将当前结点作为叶子节点，并将数据集中数量最多的类作为该结点输出类；

　　3）否则，计算所有特征的信息增益，若此时最大的信息增益小于阀值ε，则将当前结点作为叶子节点，并将数据集中数量最多的类作为该结点输出类；

　　4）若当前的最大信息增益大于阀值ε，则将最大信息增益对应的特征A作为最优划分特征对数据集进行划分，根据特征A的取值将数据集划分为若干个子集；

　　5）对第i个结点，以Di为训练集，以Ai为特征集（将之前用过的特征从特征集中去除），递归的调用前面的1- 4 步。

　　 ID3算法简单，但是其缺点也不少：

　　1）ID3算法采用信息增益来选择最优划分特征，然而人们发现，信息增益倾向与取值较多的特征，对于这种具有明显倾向性的属性，往往容易导致结果误差；

　　2）ID3算法没有考虑连续值，对与连续值的特征无法进行划分；

　　3）ID3算法无法处理有缺失值的数据；

　　4）ID3算法没有考虑过拟合的问题，而在决策树中，过拟合是很容易发生的；

　　5）ID3算法采用贪心算法，每次划分都是考虑局部最优化，而局部最优化并不是全局最优化，当然这一缺点也是决策树的缺点，获得最优决策树本身就是一个NP难题，所以只能采用局部最优；

3、C4.5算法

　　C4.5算法的提出旨在解决ID3算法的缺点 ，因此讲解C4.5算法我们从ID3算法的缺点出发：

　　1）采用信息增益比来替代信息增益作为寻找最优划分特征，信息增益比的定义是信息增益和特征熵的比值，对于特征熵，特征的取值越多，特征熵就倾向于越大；

　　　　信息增益比的表达式如下：

　　　　

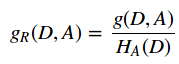
　　　　其中 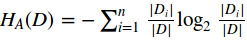 ，n是特征A取值的个数。

　　2）对于连续值的问题，将连续值离散化，在这里只作二类划分，即将连续值划分到两个区间，划分点取两个临近值的均值，因此对于m个连续值总共有m-1各划分点，对于每个划分点，依次算它们的信息增益，选取信息增益最大的点作为离散划分点；

　　3）对于缺失值的问题，我们需要解决两个问题，第一是在有缺失值的情况下如何选择划分的属性，也就是如何得到一个合适的信息增益比；第二是选定了划分属性，对于在该属性的缺失特征的样本该如何处理。

　　　　对于第一个问题，对于某一个有缺失特征值的特征A。C4.5的思路是将数据分成两部分，对每个样本设置一个权重（初始可以都为1），然后划分数据，一部分是有特征值A的数据D1，另一部分是没有特征A的数据D2. 然后对于没有缺失特征A的数据集D1来和对应的A特征的各个特征值一起计算加权重后的信息增益比，最后乘上一个系数，这个系数是无特征A缺失的样本加权后所占加权总样本的比例。

　　　　对于第二个子问题，可以将缺失特征的样本同时划分入所有的子节点，不过将该样本的权重按各个子节点样本的数量比例来分配。比如缺失特征A的样本a之前权重为1，特征A有3个特征值A1，A2，A3。 3个特征值对应的无缺失A特征的样本个数为2，3，4。则a同时划分入A1，A2，A3。对应权重调节为2/9，3/9，4/9；

　　4）对于过拟合的问题，采用了后剪枝算法和交叉验证对决策树进行剪枝处理，这个在CART算法中一起介绍。

　　虽说C4.5解决了ID3算法中的几个缺点，但其仍有很多不足之处：

　　1）C4.5的剪枝算法不够优秀；

　　2）C4.5和ID3一样，都是生成的多叉树，然而在计算机中二叉树模型会比多叉树的运算效率高，采用二叉树也许效果会更好；

　　3）在计算信息熵时会涉及到大量的对数运算，如果是连续值还需要进行排序，寻找最优离散划分点，这些都会增大模型的运算；

　　4）C4.5算法只能处理分类问题，不能处理回归问题，限制了其应用范围。

4、CART算法

　　CART树是在C4.5算法的基础上对其缺点进行改进的算法，采用二叉树作为树模型的基础结构，采用基尼指数（分类问题）和和方差（回归问题）属性来选取最优划分特征。CART算法由以下两部组成：

　　1）决策树生成：基于训练集极大可能的生成决策树（事实上，在生成树的过程中可以加入一些阀值，对决策树做一些预剪枝处理，配合之后的后剪枝效果会更好）；

　　2）决策树剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，这时用损失函数最小作为剪枝的标准（寻找全局最优子树）；

　　CART分类树

　　先引入基尼指数，基尼指数也可以表述数据集D的不确定性，基尼指数越大，样本集合的不确定性就越大，对于给定的样本集，假设有k个类别，第k个类别的概率为P_k，则基尼指数的表达式为：

　　

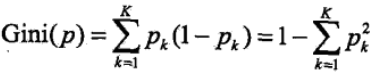
　　对于给定的样本集合D，其基尼指数可以表述为：

　　

　　在给定特征A的情况下，若集合被特征A的取值给分成D₁和D₂ ，则在特征A的条件下的基尼指数可以表述为：

　　

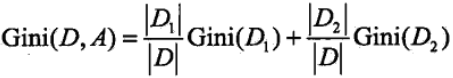
　　因此在进行最优划分特征选择时，我们选择在该特征下基尼指数最小的特征，而且在二分类的问题中基尼指数和熵的差异不大，基尼指数和熵之半的曲线如下

　　

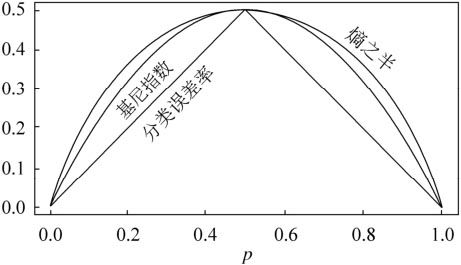
　　引入基尼指数解决了计算熵时大量的对数运算的问题，然而CART树是二叉树，那么我们在选取了特征之后，又该如何划分数据集呢？

　　1）对于连续值

　　　　在C4.5中我们对于连续值的处理就是将其划分为两类，那么在CART中更是如此，划分方式和C4.5算法一模一样，唯一的区别是度量方式不同，在CART中采用基尼指数作为度量属性，选择使得在该特征下基尼指数最小的划分点来将连续值划分为两类；

　　2）对于离散值

　　　　对与离散值的处理和ID3或者C4.5都有很大的不同，对于某个特征A，其取值可能不只两个，对于取值大于2的，我们需要随意组合将其分为两类，选择基尼指数最小的那一类作为当前的划分（因为对与特征A，并没有将其按照取值完全分开，因此此时特征A不会从特征集中去除，会留到之后可能再被选择，这也是和ID3、C4.5不同的地方）。

　　对于CART分类树的算法流程和C4.5差不多，只要注意每次都是进行二类划分，即使该特征的取值有多个。

　　CART回归树

　　CART回归树是CART算法中新引进的用来处理回归问题，其算法流程和CART分类树差不多，但在细节上有写不同，主要是以下两个方面：

　　1）对连续值的处理方式不一样，采用的特征选择属性不一样，在这里采用的是常用的和方差来进行特征选择，其表达式如下：

　　

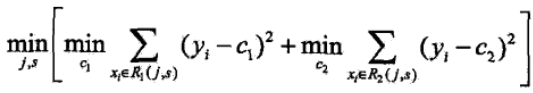
　　对于任意特征A，对应的任意划分点将数据集划分成D₁和D₂两个部分，寻找到使得D₁和D₂各自集合的均方误差最小，并且D₁和D₂的均方误差之和也最小的划分点，该划分点就是该特征最佳的划分点，因此利用和方差选取最优特征时，就是选取使得和方差最小的特征和划分点。

　　2）决策树的预测方式不一样，在分类算法中都是采用叶子结点中数量最多的类别作为输出值，而对于回归问题，一般采用叶子结点中的样本集的均值或者中位数作为输出值，有的还会基于叶子结点中的集合建立线性回归模型来作为输出值。

　　CART算法虽然在C4.5算法的基础上进行了很大的改进，但是仍然存在一些缺点：

　　1）每次用最优特征进行划分，这种贪心算法很容易陷入局部最优，事实上分类决策不应该由某一特征决定，而是一组特征决定的，比如多变量决策树（事实上我觉得还不如用集成算法）；

　　2）样本敏感性，样本的一点改动足以影响整个树的结构，也可以通过集成算法解决；

　　感觉单独的决策树算法用的不多，决策树大多是作为集成算法的基学习器来用的。

5、CART算法的剪枝

　　无论是对于分类树还是回归树，都可以用同样的方式进行剪枝，决策树是非常容易过拟合的，因此对决策树进行剪枝是很有必要的（剪枝说白了就是减小模型的复杂度），具体的剪枝算法如下：

　　首先我们看看剪枝的损失函数度量，在剪枝的过程中，对于任意的一刻子树T,其损失函数为：

　　

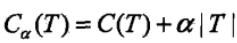
　　其中，α为正则化参数，这和线性回归的正则化一样。C(T)为训练数据的预测误差，分类树是用基尼系数度量，回归树是均方差度量。|T|是子树T的叶子节点的数量。当α=0时，即没有正则化，原始的生成的CART树即为最优子树。当α= ∞ 时，即正则化强度达到最大，此时由原始的生成的CART树的根节点组成的单节点树为最优子树。当然，这是两种极端情况。一般来说，α越大，则剪枝剪的越厉害，生成的最优子树相比原生决策树就越偏小。对于固定的α，一定存在使损失函数C_α(T)最小的唯一子树。

　　具体的从整体树开始剪枝，对与任意内部结点，以t为单结点数的损失函数是：

　　

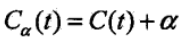
　　以t为根节点的子树T_t的损失函数是：

　　

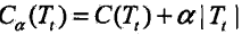
　　当α=0或者α很小时，Cα(Tt) < Cα(T) ；

　　当α增大到一定的程度时 Cα(Tt) = Cα(T)；

　　当α继续增大时不等式反向，也就是说，如果满足：α=(C(T) − C(T_t)) / (|T_t| − 1)，T_t和T有相同的损失函数，但是T节点更少，因此可以对子树T_t进行剪枝，也就是将它的子节点全部剪掉，变为一个叶子节点T。

　　最后我们看看CART树的交叉验证策略。上面我们讲到，可以计算出每个子树是否剪枝的阈值α，如果我们把所有的节点是否剪枝的值α都计算出来，然后分别针对不同的α所对应的剪枝后的最优子树做交叉验证。这样就可以选择一个最好的α，有了这个α，我们就可以用对应的最优子树作为最终结果。

　　现在我们现在来看看CART树的剪枝算法：

　　输入是CART树建立算法得到的原始决策树T；

　　输出是最优决策子树Tα；

　　具体算法过程如下：

　　1）初始化α_min = ∞， 最优子树集合ω = {T}；

　　2）从叶子节点开始自下而上计算各内部节点t的训练误差损失函数C_α(T_t)（回归树为均方差，分类树为基尼系数）， 叶子节点数|T_t|，以及正则化阈值α=min{(C(T) − C(T_t)) / (|Tt| − 1), αmin}, 更新α_min = α；

　　3) 得到所有节点的α值的集合M;

　　4）从M中选择最大的值α_k，自上而下的访问子树t的内部节点，如果(C(T) − C(Tt)) / (|Tt| − 1) ≤ α_k时，进行剪枝。并决定叶节点t的值。如果是分类树，则是概率最高的类别，如果是回归树，则是所有样本输出的均值。这样得到α_k对应的最优子树T_k

　　5）最优子树集合ω = ω ∪ T_k， M = M − {α_k};

　　6) 如果M不为空，则回到步骤4。否则就已经得到了所有的可选最优子树集合ω；

　　7) 采用交叉验证在ω选择最优子树T_α　　　

6、决策树的优缺点

　　决策树的优点：

　　1）决策树简单直观，相比于如神经网络之类的黑盒模型，决策树容易理解，还可以进行可视化；

　　2）基本上不需要做预处理，不需要做归一化，不需要处理缺失值；

　　3）使用决策树进行预测的时间复杂度只有O(log₂m)，m为样本数；

　　4）即可以处理离散值，也可以处理连续值，无论数对于分类问题还是回归问题；

　　5）可以很容易的处理多分类的问题；

　　6）可以用交叉验证来对决策数进行剪枝，避免过拟合（对于很复杂的决策树，最好配合预剪枝一起处理）；

　　7）对于异常点的容错性好，健壮性高；

　　决策树的缺点：

　　1）决策树很容易过拟合，很多时候即使进行后剪枝也无法避免过拟合的问题，因此可以通过设置树深或者叶节点中的样本个数来进行预剪枝控制；

　　2）决策树属于样本敏感型，即使样本发生一点点改动，也会导致整个树结构的变化，可以通过集成算法来解决；

　　3）寻找最优决策树是各NP难题，一般是通过启发式方法，这样容易陷入局部最优，可以通过集成算法来解决；　　

　　4）决策树无法表达如异或这类的复杂问题；