Timus 1132 Square Root(二次剩余）

http://acm.timus.ru/problem.aspx?space=1&num=1132

题意：

求 x^2 ≡ n mod p  p是质数 的 解

本题中n>=1

特判p=2，接下来求当p是奇素数时的解

引理1：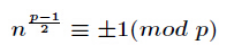

引理2：方程有解当且仅当

定理：

设a满足 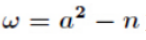不是模p的二次剩余，

即无解，

那么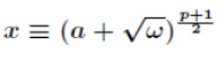是二次剩余方程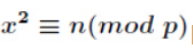的解

#include<cstdio>
#include<cstdlib>
#include<algorithm>
 
using namespace std;
 
typedef long long LL;
 
int w;
 
struct T
{
    int p,d;
};
 
int mod(LL a,int p)
{
    a%=p;
    if(a<) a+=p;
    return a;
}
 
int Pow(int a,int b,int p)
{
    int res=;
    for(;b;a=1LL*a*a%p,b>>=)
        if(b&) res=1LL*res*a%p;
    return res;
}
 
//求勒让德符号
int Legendre(int a,int p)
{
    return Pow(a,p->>,p);
}
 
//二次域上的乘法
T mul(T a,T b,int p)
{
    T ans;
    ans.p=(1LL*a.p*b.p%p+1LL*a.d*b.d%p*w%p)%p;
    ans.d=(1LL*a.p*b.d%p+1LL*a.d*b.p%p)%p;
    return ans;
}
 
//二次域上的快速幂
T power(T a,int b,int p)
{
    T ans;
    ans.p=;
    ans.d=;
    for(;b;a=mul(a,a,p),b>>=)
        if(b&) ans=mul(ans,a,p);
    return ans;
}
 
int solve(int n,int p)
{
    if(p==) return ;
    if(Legendre(n,p)+==p) return -;
    int a;
    LL t;
    while()
    {
        a=rand()%p;
        t=1LL*a*a-n;
        w=mod(t,p);
        if(Legendre(w,p)+==p) break;
    }
    T tmp;
    tmp.p=a;
    tmp.d=;
    T ans=power(tmp,p+>>,p);
    return ans.p;
}
 
int main()
{
    int t;
    scanf("%d",&t);
    int n,p;
    int a,b;
    while(t--)
    {
        scanf("%d%d",&n,&p);
        n%=p;
        a=solve(n,p);
        if(a==-)
        {
            puts("No root");
            continue;
        }
        b=p-a;
        if(a>b) swap(a,b);
        if(a==b) printf("%d\n",a);
        else printf("%d %d\n",a,b);
    }
}