C#学习笔记04--排序/查找/二维数组/交叉数组

一. 冒泡排序(重点)

思路:  每次比较把较小的放在前面, 大的放到后面;

图解:下图是最坏情况下的排序

`

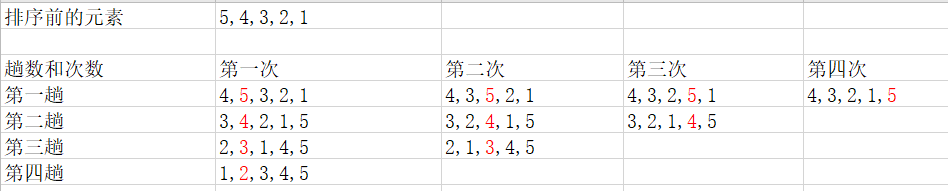
冒泡排序m个元素, 就有(m-1)趟排序, 第一趟m-1次, 第二趟 m-2次....    总结下来就是趟数加上次数就等于总的元素数;

核心算法:

            int[] intNums = new int[] { , , , ,  };
            int temp;
            for (int i = ; i < intNums.Length -  ; i++)
            {
                for (int j = ; j < intNums.Length -  - i; j++)
                {
                    if (intNums[j] > intNums[j + ])
                    {
                        temp = intNums[j];
                        intNums[j] = intNums[j + ];
                        intNums[j + ] = temp;
                    }
                }
            }
            foreach (int item in intNums)
            {
                Console.WriteLine(item);
            }

 优化:

上述我们写的代码有个很大的问题,  只有当数组初始排序是最坏情况的时候, 需要走完所有的趟数和次数. 初始排序的时候有一部分已经是有序的, 例如 {5, 1, 2, 3, 4}这样的一个顺序, 当执行完一趟的时候 我们其实已经得到了最终的结果, 没有必要再进行一趟趟的循环.

当数据量少的时候影响还不是很大, 但是如果数量上升到一定数量的时候这个时间就很可怕了. 因此我们可以对它进行一些优化; 当判断发到顺序已经排好了就可以终止循环, 那么如何来判断?

显而易见, 在一趟中没有发生任何交换的时候, 即内层for循环里的if如果没有被激活, 就代表顺序已经排好了.

如下, 我们可以用一个标签来判断:

            int[] intNums = new int[] { , , , ,  };
            int temp;
            bool tag = true; //定义一个tag标签 用来进行判断
            // 在循环条件中加了一个与运算, 如果tag为true那么就继续进行循环, 如果为false就直接终止循环, 不用使用break来终止了;
            for (int i = ; i < intNums.Length -  && tag; i++)
            {
                tag = false; // 这里是必不可少的, 如果少了那么 tag 就会一直为真, 不会提前终止循环了.
                for (int j = ; j < intNums.Length -  - i; j++)
                {
                    if (intNums[j] > intNums[j + ])
                    {
                        tag = true;
                        temp = intNums[j];
                        intNums[j] = intNums[j + ];
                        intNums[j + ] = temp;
                    }
                }
            }
            foreach (int item in intNums)
            {
                Console.WriteLine(item);
            }

二.选择排序

思路: 

以数组 array = {5, 4, 3, 2, 1}为例,:

第一趟用第一个元素和剩下的元素比较大小, 找到最小的数, 然后把它的下标和值记录下来, 这一趟结束后将其和第一个元素进行交换;

第二趟用第二元素和它之后的元素进行比较, 找到最小值, 最后再进行交换, 然后以此类推.

总的来说就是, 没有找到数组中最小的数,它依次放到前面来.

图解:

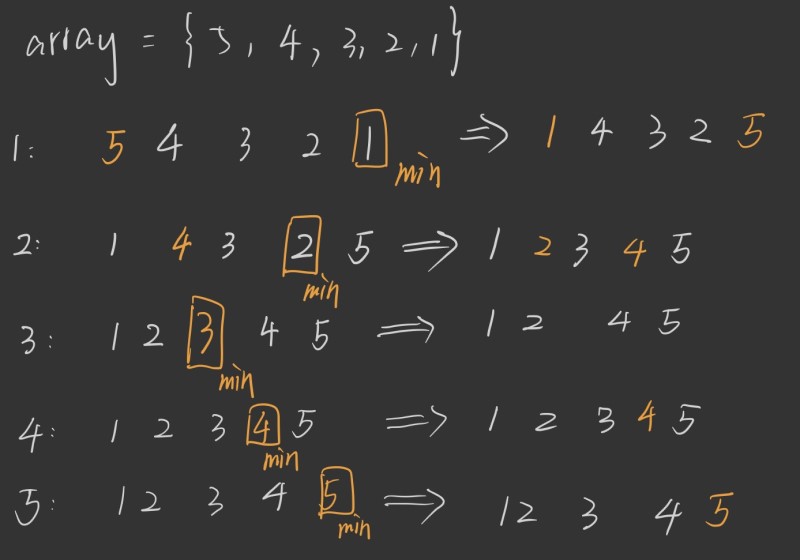
核心算法:

            int[] array = new int[] { , , , ,  };

            for (int i = ; i < array.Length - ; i++)
            {
                int min = array[i]; // min用来存放最小值
                int index = i; // index就用来存放最小值的下标
                for (int j = i + ; j <= array.Length - ; j++)
                {
                    if (min > array[j])
                    {
                        min = array[j];
                        index = j;
                    }
                }
                array[index] = array[i];
                array[i] = min;

            }
            foreach (int item in array)
            {
                Console.Write(item + " ");
            }    

三.二分查找

查找元素是经常会用到的, 通常没有任何技巧的查找方法就是一个个遍历, 对比我们的期望元素. 这种查找方法有一个非常致命的缺点, 如果数据量过于庞大, 对性能的消耗非常大;

说明:二分查找又称为折半查找, 这种查找是有前提的:要查找的数组必须是有序的, 升序和降序均可; 以升序数组为例, 首先拿到已知元素(num)与数组中间位置的元素(mid)进行比较, 如果 mid > num, 说明 mid右边的数一定都比num大, 那么就可以把mid右边的数都pass, 直接从mid 左边的数里查找有没有num. 同理, 如果mid < num , 就说明mid左边的数都小于num , 就可以把它们都pass了. 这样反反复复知道查找到num为止.

图解:

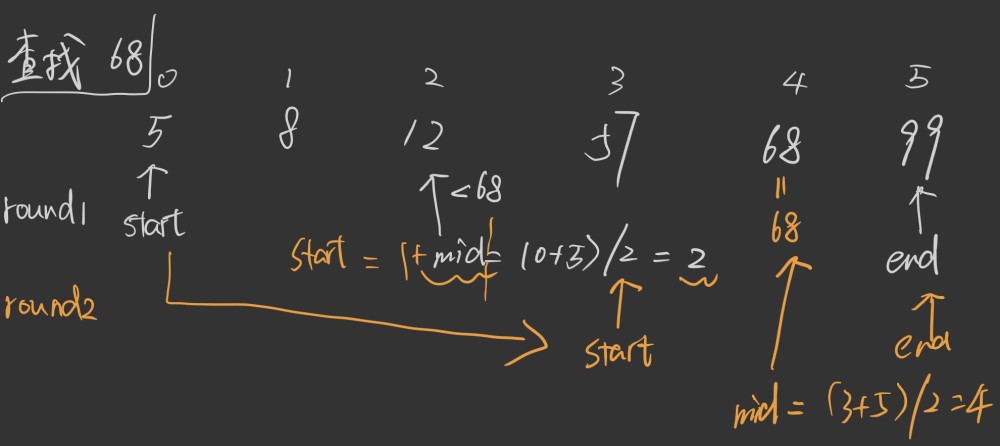
核心算法:

            int[] sortNums = new int[] { , , , , , ,  };
            int start = , end = sortNums.Length - ; // 定义开头和结尾的旗
            Console.WriteLine("请输入你想要查找的数:");
            int num = int.Parse(Console.ReadLine());
            while(start <= end) // 如果start > end说明num不在 查找的数组里
            {

                int mid = (start + end) / ; // 每次都是开头结尾中间的元素和num比较
                if (sortNums[mid] > num)
                {
                    end = mid - ;

                }
                else if(sortNums[mid] < num)
                {
                    start = mid + ;
                }
                else
                {
                    Console.WriteLine("查到了, 在第 {0} 个位置", mid + );
                    break;
                }
            }
            if (start > end)
            {
                Console.WriteLine("对不起元素没有找到.");
            }

四.二维数组(重点)

4.1二维数组的声明和初始化

声明

数据类型[,] = new 数据类型[行数, 列数];

初始化 : 分为动态初始化和静态初始化 , 花括号里面的各个花括号代表一行

第一种动态初始化:

int[, ] array = new int[, ] {{, , }, {, , }};

第二种动态初始化:

int[, ] array = new int[, ]  {{, , }, {, , }};

静态初始化:

int[, ] array = {{, , }, {, , }};

注意: 二维数组静态初始化定义时, 行数的个数可以是任意的, 但是列数的个数必须是相同的, 即 每个内层花括号中元素的个数必要要相同.

4.2 二维数组的遍历

C#中通过 GetLength方法可以得到二维数组的行数和列数

array.GetLength(0)  得到有多少行数;

array.GetLength(1) 得到有多少列数;

int[,] array = new int[, ] { { , ,  }, { , ,  } };
for(int i = ; i < array.GetLength(); i++)
{
       for(int j = ; j < array.GetLength(); j++)
       {
            Console.Write(array[i, j] + " " );
       }
        Console.WriteLine();
}

 

练习

1.定义一个数组, 将该数组的转置存到另一个数组中;

            int[,] array = new int[, ] { { , ,  }, { , ,  } };
            int[,] newArray = new int[array.GetLength(1), array.GetLength(0)];
             for(int i = ; i < array.GetLength(); i++)
            {
                for(int j = ; j < array.GetLength(); j++)
                {
                    newArray[j, i] = array[i, j];
                }
            }

            Console.WriteLine("转置为:");
            for (int i = ; i < newArray.GetLength(); i++)
            {
                for (int j = ; j < newArray.GetLength(); j++)
                {
                    Console.Write(newArray[i, j] + " ");
                }
                Console.WriteLine();
            }     

2.有一个3行4列的二维数组, 要求编程找出最大元素, 并输出所在的行和列.

           int[,] array = new int[,] { { , , ,  }, { , , ,  }, { , , ,  } };
            int max = array[, ], r = , c = ;
            for (int i = ; i < array.GetLength(); i++)
            {
                for (int j = ; j < array.GetLength(); j++)
                {
                    if(max < array[i, j])
                    {
                        max = array[i, j];
                        r = i;
                        c = j;
                    }
                }
            }
            Console.WriteLine("最大值为: {0}, 在{1}行 {2}列", max, r+, c+);

五.交错数组

5.1 交错数组中包含一维数组

声明:

int[][] array = new int[行数][列数];   行数必须写, 但是列数可以不写

初始化:

int[][] array = new int[][];
array[] = new int[] { , , ,  };
array[] = new int[] { , ,  };
array[] = new int[] { ,  };
// 赋值的时候必须动态赋值

int[][] array1 =
{
new int[] {1, 2, 3},
new int[] {3, 4, 5,6}
};

取值:

直接把写上行号和列号就可以, 例如, 如果我们要取 array1 中的元素2, 就可以写 array1[0][1];

遍历:

交错数组的遍历要比二维数组更简单一些, 交错数组可以被拆分开

            int[][] array = new int[][];
            array[] = new int[] { , , ,  };
            array[] = new int[] { , ,  };
            array[] = new int[] { ,  };

            for(int i = ; i < array.Length; i++)
            {
                for(int j = ; j < array[i].Length; j++)
                {
                    Console.Write(array[i][j] + " " );
                }
                Console.WriteLine();
            }

5.2 交错数组中包含二维数组

这个直接上代码会比较清晰

声明:

取值:

遍历: