SDOI2012 走迷宫
走迷宫
Morenan被困在了一个迷宫里。迷宫可以视为N个点M条边的有向图，其中Morenan处于起点S，迷宫的终点设为T。可惜的是，Morenan非常的脑小，他只会从一个点出发随机沿着一条从该点出发的有向边，到达另一个点。这样，Morenan走的步数可能很长，也可能是无限，更可能到不了终点。若到不了终点，则步数视为无穷大。但你必须想方设法求出Morenan所走步数的期望值。
N<=10000，M<=1000000，保证强连通分量的大小不超过100
Clove_unique的题解
首先考虑图是一个DAG的情况
如果除了终点之外还有出度为0的点，那么答案为INF。因为有概率不走到终点，无穷级数里面有∞。
然后令f(i)表示从点i走到终点的期望步数，那么f(i)=∑(i,v)∈E(f(v)+1)、∗out(i)，其中out(i)从点i走一条边的概率（也就是出度的倒数）。
如果图不是一个DAG的话，可以缩点之后将图变成一个DAG，对于DAG上的边直接dp，但是强连通分量里的点可以互相到达，这实际上就是列出了一些方程然后高斯消元。
CO LD inf=1e18,eps=1e-12;
CO int N=10000+10,M=100+10;
vector<int> to[N],rto[N];
LD out[N];
int pos[N],dfn,low[N];
int stk[N],top,ins[N];
int bln[N],idx;
vector<int> scc[N];
void tarjan(int u){
pos[u]=low[u]=++dfn;
stk[++top]=u,ins[u]=1;
for(int i=0;i<(int)to[u].size();++i){
int v=to[u][i];
if(!pos[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(ins[v]) low[u]=min(low[u],pos[v]);
}
if(low[u]==pos[u]){
++idx;
int x;
do{
x=stk[top--],ins[x]=0;
bln[x]=idx,scc[idx].push_back(x);
}while(x!=u);
}
}
bool vis[N];
void dfs(int u){
vis[u]=1;
for(int i=0;i<(int)to[u].size();++i){
int v=to[u][i];
if(!vis[v]) dfs(v);
}
}
int in[N],tmp[N];
LD f[N],a[M][M];
void gauss(int n){
for(int i=1;i<=n;++i){
int p=i;
for(int j=i+1;j<=n;++j)
if(abs(a[j][i])>abs(a[p][i])) p=j;
if(p!=i) swap(a[p],a[i]);
for(int j=1;j<=n;++j)if(j!=i and abs(a[j][i])>eps){
double coef=-a[j][i]/a[i][i];
for(int k=i;k<=n+1;++k) a[j][k]+=coef*a[i][k];
}
}
for(int i=1;i<=n;++i) a[i][n+1]/=a[i][i],a[i][i]=1;
}
int main(){
int n=read<int>(),m=read<int>(),s=read<int>(),t=read<int>();
while(m--){
int u=read<int>(),v=read<int>();
to[u].push_back(v),rto[v].push_back(u);
++out[u];
}
for(int i=1;i<=n;++i) out[i]=1/out[i];
for(int i=1;i<=n;++i)
if(!pos[i]) tarjan(i);
dfs(s);
if(!vis[t]){
puts("INF");
return 0;
}
for(int u=1;u<=n;++u)
for(int i=0;i<(int)rto[u].size();++i){
int v=rto[u][i];
if(bln[u]!=bln[v]) ++in[bln[v]];
}
for(int i=1;i<=idx;++i)if(i!=bln[t])
if(!in[i]){
puts("INF");
return 0;
}
deque<int> Q(1,bln[t]);
while(Q.size()){
int x=Q.front();Q.pop_front();
memset(a,0,sizeof a);
int num=scc[x].size();
// cerr<<"scc="<<endl;
// for(int i=1;i<=num;++i) cerr<<" "<<scc[x][i-1];
// cerr<<endl;
for(int i=1;i<=num;++i) tmp[scc[x][i-1]]=i;
for(int i=1;i<=num;++i){
int u=scc[x][i-1];
a[i][i]=1,a[i][num+1]=f[u];
if(u==t) continue;
for(int j=0;j<(int)to[u].size();++j){
int v=to[u][j];
if(bln[v]!=bln[u]) continue;
a[i][tmp[v]]-=out[u],a[i][num+1]+=out[u];
}
}
gauss(num);
for(int i=1;i<=num;++i){
int u=scc[x][i-1];
f[u]=a[i][num+1];
for(int j=0;j<(int)rto[u].size();++j){
int v=rto[u][j];
if(bln[v]!=x){
if(--in[bln[v]]==0) Q.push_back(bln[v]);
f[v]+=(f[u]+1)*out[v];
}
}
}
}
printf("%.3Lf\n",f[s]);
return 0;
}
Fox Rocks
Mr. Fox sure loves his rocks! In fact, when he's not in a hurry, he often looks at the rocks lying around near him to decide where to wander in his forest.
Mr. Fox lives in a forest with \(N\) clearings, numbered from \(0\) to \(N-1\), with \(P\) one-way trails initially running amongst them. The \(i\)th trail runs from clearing \(A_i\) to a different clearing \(B_i\), and is littered with \(R_i\) rocks. No two clearings are connected by multiple trails running in the same direction, though they could be connected by 2 trails running in opposite directions. Additionally, an interesting property of this forest is that a trail from clearing \(a\) to clearing \(b\) may only exist if \(0 ≤ \lfloor\frac{b}{4}\rfloor - \lfloor\frac{a}{4}\rfloor ≤ 1\).
To entertain himself over a period of \(D\) days, Mr. Fox will cause one event to occur on each day. The \(i\)th event may be one of 3 types, determined by the value of \(E_i\):
Given 3 integers \(X_i, Y_i\), and \(Z_i\), Mr. Fox will create a new trail from clearing \(X_i\) to a different clearing \(Y_i\), and drop \(Z_i\) rocks onto it. It's guaranteed that no trail from \(X_i\) to \(Y_i\) will exist at the start of the \(i\)th day, and that \(0 ≤ \lfloor\frac{X_i}{4}\rfloor - \lfloor\frac{Y_i}{4}\rfloor ≤ 1\) will hold.
Given 2 distinct integers \(X_i\) and \(Y_i\), Mr. Fox will completely destroy the trail from clearing \(X_i\) to clearing \(Y_i\) (which is guaranteed to exist at the start of the \(i\)th day). Note that, once such a trail is destroyed, a new trail from \(X_i\) to \(Y_i\) may be created in the future.
Given 2 distinct integers \(X_i\) and \(Y_i\), Mr. Fox will take a "random stroll" starting at clearing \(X_i\), and would like to determine the probability that he'll visit clearing \(Y_i\) at least once during it.
A "random stroll" consists of repeating the following process potentially infinitely: If Mr. Fox is currently in some clearing \(c\), and there are no outgoing trails from \(c\), then the stroll ends immediately. Otherwise, he'll consider all of the rocks on all of the outgoing trails from \(c\), choose one of these rocks uniformly at random, follow the trail on which that rock lies to its destination clearing (without removing any rocks), and repeat the process from his new clearing.
For each event of type 3, output the requested probability.
\(1 ≤ T ≤ 20, 1 ≤ N ≤ 50,000, 0 ≤ P ≤ 100,000, 1 ≤ D ≤ 20,000\)
题解
性质分析
首先把算概率转化成算经过次数的期望。每个点的期望定义式是
\]
把题目所给的DAG套SCC的图按除以 \(4\) 下取整分块，显然每个点的期望只可能与到它有边的前一块或同一块的点有关。该如何利用这一性质呢？
考虑暴力的做法。我们先对起点所在的块进行解方程，算出块内每一个点的期望。然后把它们的期望看成常数，用它们的期望去更新下一块内点的期望方程的常数项。接着对下一块进行同样的操作即可。
现在我们要加速这一递推的过程。注意到一段连续块内期望的转移只与连边情况有关，在没有修改的情况下是固定的。
算法设计
我们可以使用主元法，把连续段头的那一块里的点的期望看成未知变量，将连续段尾的那一块里的每个点的期望用这些未知变量表示出来。这样合并两连续块段 \([l,mid],[mid+1,r]\) 的时候只需要把第 \(mid+1\) 块设的未知变量用第 \(l\) 块设的位置变量解出来，并带入第 \(r\) 块的系数向量，即可将第 \(r\) 块里的点的期望用第 \(l\) 块里点的期望表示出来。
用线段树来维护这个快速递推。询问的时候只需要把起点所在块内每个点的期望解出来，然后用线段树快速递推到终点所在块的前一块，最后暴力递推终点所在块的期望即可。
细节处理
考虑下面这组数据：
1
4 4 1
0 1 1
0 3 1
1 2 1
2 1 1
3 0 3
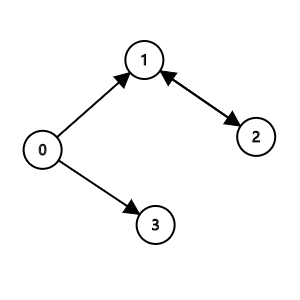
现在要算从 \(0\) 号节点出发走到 \(3\) 号节点的概率，显然它是 \(0.5\)。
但是我的程序会输出nan，这是因为 \(1,2\) 号节点的期望其实是 \(\infty\)，然后高斯消元就会出现某主元找不到系数非 \(0\) 行等等问题。
我的解决方法是额外维护每个点能不能直接或间接的走到下一块中去，如果不能的话直接钦定它的期望为 \(0\)。因为它不会对后面的点有贡献，所以这样做没有问题。
时间复杂度 \(O(64m\log \lfloor\frac{n}{4}\rfloor)\)。
struct node{LD v[4];};
node operator*(node a,LD k){
for(int i=0;i<=3;++i) a.v[i]*=k;
return a;
}
node operator/(node a,LD k){
for(int i=0;i<=3;++i) a.v[i]/=k;
return a;
}
node operator+(node a,CO node&b){
for(int i=0;i<=3;++i) a.v[i]+=b.v[i];
return a;
}
CO int N=50000+10;
LD edge[N][2][4],out[N];
namespace T{
int vis[N];
node coef[N][4];
LD a[4][4];node b[4];
#define lc (x<<1)
#define rc (x<<1|1)
void dfs(int u){ // search valid points
if(vis[u]) return;
vis[u]=1;
for(int i=0;i<=3;++i)if(edge[u][0][i]) dfs(4*(u/4)+i);
}
void push_up(int x,int l,int r){
int mid=(l+r)>>1;
memset(a,0,sizeof a),memset(b,0,sizeof b);
for(int i=0;i<=3;++i)if(vis[4*(mid+1)+i]) // mid+1
for(int j=0;j<=3;++j)if(edge[4*(mid+1)+i][1][j]) // mid
b[i]=b[i]+coef[lc][j]*edge[4*(mid+1)+i][1][j]/out[4*mid+j];
for(int i=0;i<=3;++i){
a[i][i]=1;
if(!vis[4*(mid+1)+i]) continue;
for(int j=0;j<=3;++j)if(edge[4*(mid+1)+i][0][j])
a[i][j]-=edge[4*(mid+1)+i][0][j]/out[4*(mid+1)+j];
}
for(int i=0;i<=3;++i){
int p=i;
for(int j=i+1;j<=3;++j)
if(abs(a[j][i])>abs(a[p][i])) p=j;
if(p!=i) swap(a[p],a[i]),swap(b[p],b[i]);
for(int j=0;j<=3;++j)if(j!=i){
b[j]=b[j]+b[i]*-a[j][i]/a[i][i]; // edit 4: gauss precision
for(int k=3;k>=i;--k) a[j][k]+=a[i][k]*-a[j][i]/a[i][i];
}
}
for(int i=0;i<=3;++i) b[i]=b[i]/a[i][i],a[i][i]=1;
memset(coef[x],0,sizeof coef[x]);
for(int i=0;i<=3;++i)if(vis[4*r+i])
for(int j=0;j<=3;++j)if(vis[4*(mid+1)+j])
coef[x][i]=coef[x][i]+b[j]*coef[rc][i].v[j];
}
void build(int x,int l,int r){
if(l==r){
memset(vis+4*l,0,4*sizeof(int));
for(int i=0;i<=3;++i)for(int j=0;j<=3;++j)
if(edge[4*(l+1)+i][1][j]) dfs(4*l+j);
memset(coef[x],0,sizeof coef[x]);
for(int i=0;i<=3;++i) coef[x][i].v[i]=vis[4*l+i]?1:0;
return;
}
int mid=(l+r)>>1;
build(lc,l,mid),build(rc,mid+1,r);
push_up(x,l,r);
}
void change(int x,int l,int r,int p){
if(l==r){
memset(vis+4*l,0,4*sizeof(int));
for(int i=0;i<=3;++i)for(int j=0;j<=3;++j)
if(edge[4*(l+1)+i][1][j]) dfs(4*l+j);
memset(coef[x],0,sizeof coef[x]);
for(int i=0;i<=3;++i) coef[x][i].v[i]=vis[4*l+i]?1:0;
return;
}
int mid=(l+r)>>1;
if(p<=mid) change(lc,l,mid,p);
else change(rc,mid+1,r,p);
push_up(x,l,r);
}
vector<node> query(int x,int l,int r,int ql,int qr){
if(ql<=l and r<=qr) return vector<node>(coef[x],coef[x]+4);
int mid=(l+r)>>1;
if(qr<=mid) return query(lc,l,mid,ql,qr);
if(ql>mid) return query(rc,mid+1,r,ql,qr);
vector<node> left=query(lc,l,mid,ql,mid),
right=query(rc,mid+1,r,mid+1,qr); // edit 3: ql,qr
memset(a,0,16*sizeof(LD)),memset(b,0,sizeof b);
for(int i=0;i<=3;++i)if(vis[4*(mid+1)+i]) // mid+1
for(int j=0;j<=3;++j)if(edge[4*(mid+1)+i][1][j]) // mid
b[i]=b[i]+left[j]*edge[4*(mid+1)+i][1][j]/out[4*mid+j];
for(int i=0;i<=3;++i){
a[i][i]=1;
if(!vis[4*(mid+1)+i]) continue;
for(int j=0;j<=3;++j)if(edge[4*(mid+1)+i][0][j])
a[i][j]-=edge[4*(mid+1)+i][0][j]/out[4*(mid+1)+j];
}
for(int i=0;i<=3;++i){
int p=i;
for(int j=i+1;j<=3;++j)
if(abs(a[j][i])>abs(a[p][i])) p=j;
if(p!=i) swap(a[p],a[i]),swap(b[p],b[i]);
for(int j=0;j<=3;++j)if(j!=i){
b[j]=b[j]+b[i]*-a[j][i]/a[i][i];
for(int k=3;k>=i;--k) a[j][k]+=a[i][k]*-a[j][i]/a[i][i];
}
}
for(int i=0;i<=3;++i) b[i]=b[i]/a[i][i],a[i][i]=1;
vector<node> ans(4);
for(int i=0;i<=3;++i)if(vis[4*qr+i]) // edit 2: qr
for(int j=0;j<=3;++j)if(vis[4*(mid+1)+j])
ans[i]=ans[i]+b[j]*right[i].v[j];
return ans;
}
#undef lc
#undef rc
}
int vis[N];
LD a[4][5],b[4];
void dfs(int u){ // search valid points
if(vis[u]) return;
vis[u]=1;
for(int i=0;i<=3;++i)if(edge[u][0][i]) dfs(4*(u/4)+i);
}
void real_main(int cas){
if(cas>1) puts("");
printf("Case #%d: ",cas);
int n=read<int>(),m=read<int>(),q=read<int>();
n+=4-n%4;
memset(edge,0,(n+4)*8*sizeof(LD)),memset(out,0,(n+4)*sizeof(LD)); // edit 5: init
while(m--){
int u=read<int>(),v=read<int>(),w=read<int>();
edge[v][v/4>u/4][u%4]=w,out[u]+=w;
}
T::build(1,0,n/4-1);
while(q--){
int opt=read<int>();
if(opt==1){
int u=read<int>(),v=read<int>(),w=read<int>();
edge[v][v/4>u/4][u%4]=w,out[u]+=w;
T::change(1,0,n/4-1,u/4);
}
else if(opt==2){
int u=read<int>(),v=read<int>();
out[u]-=edge[v][v/4>u/4][u%4],edge[v][v/4>u/4][u%4]=0;
T::change(1,0,n/4-1,u/4);
}
else{
int u=read<int>(),v=read<int>();
if(u/4>v/4){
printf("0.000000 ");
continue;
}
if(u/4==v/4){
memset(vis+4*(u/4),0,4*sizeof(int));
dfs(v);
for(int i=0;i<=3;++i)for(int j=0;j<=3;++j)
if(edge[4*(u/4+1)+i][1][j]) dfs(4*(u/4)+j);
memset(a,0,20*sizeof(LD)),a[u%4][4]=1;
for(int i=0;i<=3;++i){
a[i][i]=1;
if(!vis[4*(u/4)+i]) continue; // edit 1: T's vis
for(int j=0;j<=3;++j)if(j!=v%4 and edge[4*(u/4)+i][0][j])
a[i][j]-=edge[4*(u/4)+i][0][j]/out[4*(u/4)+j];
}
for(int i=0;i<=3;++i){
int p=i;
for(int j=i+1;j<=3;++j)
if(abs(a[j][i])>abs(a[p][i])) p=j;
if(p!=i) swap(a[p],a[i]);
for(int j=0;j<=3;++j)if(j!=i){
LD c=-a[j][i]/a[i][i];
for(int k=i;k<=4;++k) a[j][k]+=a[i][k]*c;
}
}
printf("%.6Lf ",a[v%4][4]/a[v%4][v%4]);
continue;
}
memset(a,0,sizeof a),a[u%4][4]=1;
for(int i=0;i<=3;++i){
a[i][i]=1;
if(!T::vis[4*(u/4)+i]) continue;
for(int j=0;j<=3;++j)if(edge[4*(u/4)+i][0][j])
a[i][j]-=edge[4*(u/4)+i][0][j]/out[4*(u/4)+j];
}
for(int i=0;i<=3;++i){
int p=i;
for(int j=i+1;j<=3;++j)
if(abs(a[j][i])>abs(a[p][i])) p=j;
if(p!=i) swap(a[p],a[i]);
for(int j=0;j<=3;++j)if(j!=i)
for(int k=4;k>=i;--k) a[j][k]+=a[i][k]*-a[j][i]/a[i][i];
}
for(int i=0;i<=3;++i) a[i][4]/=a[i][i],a[i][i]=1;
vector<node> mid=T::query(1,0,n/4-1,u/4,v/4-1);
memset(b,0,4*sizeof(LD));
for(int i=0;i<=3;++i)if(T::vis[4*(v/4-1)+i])
for(int j=0;j<=3;++j)if(T::vis[4*(u/4)+j])
b[i]+=a[j][4]*mid[i].v[j];
memset(vis+4*(v/4),0,4*sizeof(int));
dfs(v);
for(int i=0;i<=3;++i)for(int j=0;j<=3;++j)
if(edge[4*(v/4+1)+i][1][j]) dfs(4*(v/4)+j);
memset(a,0,20*sizeof(LD));
for(int i=0;i<=3;++i)
for(int j=0;j<=3;++j)if(edge[4*(v/4)+i][1][j])
a[i][4]+=b[j]*edge[4*(v/4)+i][1][j]/out[4*(v/4-1)+j];
for(int i=0;i<=3;++i){
a[i][i]=1;
if(!vis[4*(v/4)+i]) continue;
for(int j=0;j<=3;++j)if(j!=v%4 and edge[4*(v/4)+i][0][j])
a[i][j]-=edge[4*(v/4)+i][0][j]/out[4*(v/4)+j];
}
for(int i=0;i<=3;++i){
int p=i;
for(int j=i+1;j<=3;++j)
if(abs(a[j][i])>abs(a[p][i])) p=j;
if(p!=i) swap(a[p],a[i]);
for(int j=0;j<=3;++j)if(j!=i)
for(int k=4;k>=i;--k) a[j][k]+=a[i][k]*-a[j][i]/a[i][i];
}
printf("%.6Lf ",a[v%4][4]/a[v%4][v%4]);
}
}
}
int main(){
// freopen("Gym.in","r",stdin),freopen("Gym.out","w",stdout);
int T=read<int>();
for(int i=1;i<=T;++i) real_main(i);
return 0;
}
一些代码调试杂谈：
这道题的线段树合并实在太复杂，以至于我必须把
push_up和query的合并分开单独实现。我以前写的线段树询问递归的时候直接传的ql,qr，在这道题里面就吃了大亏。以后要换成现在这种实现方式了。高斯消元的不同写法有精度问题，解决方法是尽量不用中间变量，先乘后除。
为了方便实现我把
n补齐到了4的倍数。由于算vis的时候需要用到下一块的反向边，所以初始化的时候需要把前n+4个位置清空了。（造数据的能把我这个卡掉，真是佩服。）
鉴于这题的小样例怎么写都能过，没有数据给你调，所以需要自己写对拍。暴力程序：
CO int N=100+10;
int n;
int edge[N][N],out[N];
int vis[N];
LD arr[N][N];
void dfs(int u){
if(vis[u]) return;
vis[u]=1;
for(int v=0;v<n;++v)if(edge[v][u]) dfs(v);
}
void real_main(int cas){
if(cas>1) puts("");
printf("Case #%d: ",cas);
read(n);
int m=read<int>(),q=read<int>();
memset(edge,0,sizeof edge),memset(out,0,sizeof out);
while(m--){
int u=read<int>(),v=read<int>(),w=read<int>();
edge[u][v]=w,out[u]+=w;
}
while(q--){
int opt=read<int>();
if(opt==1){
int u=read<int>(),v=read<int>(),w=read<int>();
edge[u][v]=w,out[u]+=w;
}
else if(opt==2){
int u=read<int>(),v=read<int>();
out[u]-=edge[u][v],edge[u][v]=0;
}
else{
int u=read<int>(),v=read<int>();
memset(vis,0,sizeof vis);
dfs(v);
memset(arr,0,sizeof arr),arr[u][n]=1;
for(int i=0;i<n;++i){
arr[i][i]=1;
if(!vis[i]) continue;
for(int j=0;j<n;++j)if(edge[j][i] and j!=v)
arr[i][j]-=(LD)edge[j][i]/out[j];
}
for(int i=0;i<n;++i){
int p=i;
for(int j=i+1;j<n;++j)
if(abs(arr[j][i])>abs(arr[p][i])) p=j;
if(p!=i) swap(arr[p],arr[i]);
for(int j=0;j<n;++j)if(j!=i)
for(int k=n;k>=i;--k) arr[j][k]+=arr[i][k]*-arr[j][i]/arr[i][i];
}
printf("%.6Lf ",arr[v][n]/arr[v][v]);
}
}
}
int main(){
// freopen("Gym.in","r",stdin),freopen("Gbf.out","w",stdout);
int T=read<int>();
for(int i=1;i<=T;++i) real_main(i);
return 0;
}
这题算是刷新了我对高斯消元的认知。
SDOI2012 走迷宫的更多相关文章
- BZOJ 2707: [SDOI2012]走迷宫( tarjan + 高斯消元 )
数据范围太大不能直接高斯消元, tarjan缩点然后按拓扑逆序对每个强连通分量高斯消元就可以了. E(u) = 1 + Σ E(v) / degree(u) 对拍时发现网上2个程序的INF判断和我不一 ...
- BZOJ 2707: [SDOI2012]走迷宫 [高斯消元 scc缩点]
2707: [SDOI2012]走迷宫 题意:求s走到t期望步数,\(n \le 10^4\),保证\(|SCC| \le 100\) 求scc缩点,每个scc高斯消元,scc之间直接DP 注意每次清 ...
- 【BZOJ2707】[SDOI2012]走迷宫 Tarjan+拓扑排序+高斯消元+期望
[BZOJ2707][SDOI2012]走迷宫 Description Morenan被困在了一个迷宫里.迷宫可以视为N个点M条边的有向图,其中Morenan处于起点S,迷宫的终点设为T.可惜的是,M ...
- bzoj 2707 [SDOI2012]走迷宫（SCC+高斯消元）
Description Morenan被困在了一个迷宫里.迷宫可以视为N个点M条边的有向图,其中Morenan处于起点S,迷宫的终点设为T.可惜的是,Morenan非常的脑小,他只会从一个点出发随机沿 ...
- BZOJ2707 [SDOI2012]走迷宫 【概率dp + tarjan + 高斯消元】
题目 Morenan被困在了一个迷宫里.迷宫可以视为N个点M条边的有向图,其中Morenan处于起点S,迷宫的终点设为T.可惜的是,Morenan非常的脑小,他只会从一个点出发随机沿着一条从该点出发的 ...
- [SDOI2012]走迷宫 （强连通分量缩点，动态规划，高斯消元）
题面 Morenan被困在了一个迷宫里.迷宫可以视为N个点M条边的有向图,其中Morenan处于起点S,迷宫的终点设为T.可惜的是,Morenan非常的脑小,他只会从一个点出发随机沿着一条从该点出发的 ...
- bzoj2702[SDOI2012]走迷宫
题意:给你一个有向图,点数10000,边数1000000,SCC大小不超过100(按数据范围的写法只有第三部分数据满足这个条件,不过第二部分数据并没有出现大小大于100个点的SCC,我是用数组大小为1 ...
- BZOJ.2707.[SDOI2012]走迷宫(期望 Tarjan 高斯消元)
题目链接 一个点到达终点的期望步数 \(E_i=\sum_{(i,j)\in G}\frac{E_j+1}{out[i]}\),\(out[i]\)为点\(i\)的出度. 那么对于一个DAG可以直接在 ...
- BZOJ2707: [SDOI2012]走迷宫(期望 tarjan 高斯消元)
题意 题目链接 Sol 设\(f[i]\)表示从\(i\)走到\(T\)的期望步数 显然有\(f[x] = \sum_{y} \frac{f[y]}{deg[x]} + 1\) 证明可以用全期望公式. ...
随机推荐
- 【视频开发】【计算机视觉】相机标定（Camera calibration）《二》
简介 摄像机标定(Camera calibration)简单来说是从世界坐标系换到图像坐标系的过程,也就是求最终的投影矩阵 P 的过程,下面相关的部分主要参考UIUC的计算机视觉的课件(网址Sprin ...
- Linux简介和各发行版介绍
一.Linux 简介 Linux 内核最初只是由芬兰人李纳斯·托瓦兹(Linus Torvalds)在大学上学时出于个人爱好而编写的. Linux 是一套免费使用和自由传播的类 Unix 操作系统,是 ...
- maven site 命令报错
在执行 mvn site 命令时报错: java.lang.NoClassDefFoundError: org/apache/maven/doxia/siterenderer/DocumentCont ...
- osx或windows系统下，用ftp上传文件到阿里云虚拟主机脚本
某天突然发现,一直在用的ftp工具并不好用,操作界面太过繁琐,而且不太稳定.于是自己找资料,整合了几句虽然简单,但是方便的代码. mac脚本 #从本地向FTP批量上传文档 需要赋予该.shell文件权 ...
- 【java】获取客户端访问的公网ip和归属地
import com.alibaba.druid.support.json.JSONUtils; import org.thymeleaf.util.StringUtils; import javax ...
- 你不知道的js——数组 join
你可能对使用数组的 join 方法已经轻车熟路,但你也许不知道: 10.If element0 is undefined or null, let R be the empty String; oth ...
- Java学习：List接口
List接口 java.util.list接口 extends Collection接口 List接口的特点: 有序的集合,存储元素和取出元素的顺序是一致的(存储123 取出123) 有索引,包含了一 ...
- 封装：WPF基于MediaElement封装的视频播放器
原文:封装:WPF基于MediaElement封装的视频播放器 一.目的:应用MediaElement创建媒体播放器 二.效果图 三.目前支持功能 播放.暂停.停止.快进.快退.声音大小.添加播放列表 ...
- SAP销售订单需求类型的确定优秀级
需求类型的确定优秀级:1.策略组里的需求类型:2.MRP组里的:3.SO行项目类别+MRP类型4.SO行项目类别 部分截图:
- 阿里云RDS数据库sql server 导入数据并添加作业小结
在阿里云购买ECS服务器和RDS数据库时,要注意网络类型要一致,最好都是VPC,否则ECS不能在内网访问RDS,只能从外网访问:在RDS控制台左侧,数据库安全性的IP白名单中添加ECS外网IP:在数据 ...