目前决定cluster数目的常用方法是手动地决定cluster的数目

哪个K是正确的?

上图中的数据集，我们可以说它有4个clusters，也可以说它有2个clusters,但哪个是正确答案呢？其实这儿没有正确答案，数据集要划分的cluster的数目本来就是模拟两可的，可以是2个，3个，4个。这也是无监督学习的一部分，因为我们的数据集没有标签，所以没有清晰的答案。所以做一个能自动求出K值的算法是非常困难的

通过肘部法则(elbow method)来选择K值

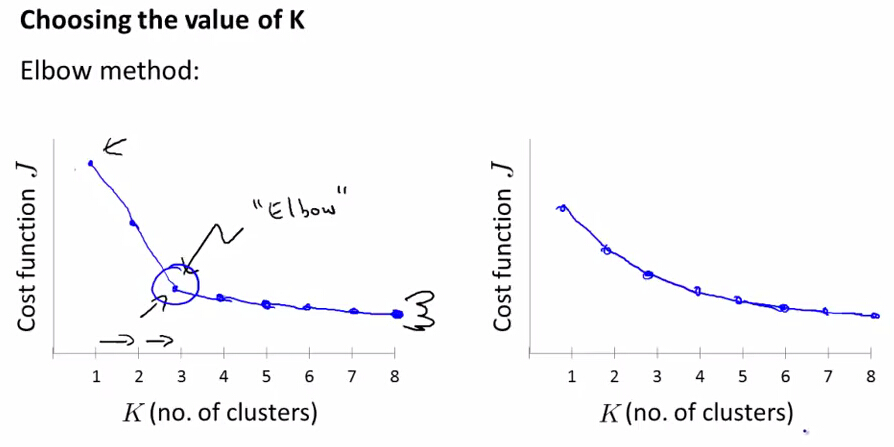
通过画K与cost function的关系曲线图，如左图所示，肘部的值(cost function开始时下降很快，在肘部开始平缓了)做为K值，K=3。

并不是所有的问题都可以通过画肘部图来解决，有的问题如右边的那个图，肘点位置不明显（肘点可以是3，4，5），这时就无法确定K值了。

故肘部图是可以尝试的一种方法，但是并不是对所有的问题都能画出如左边那么好的图来确定K值。

另一种选择K值的方法—后续目的(市场等)

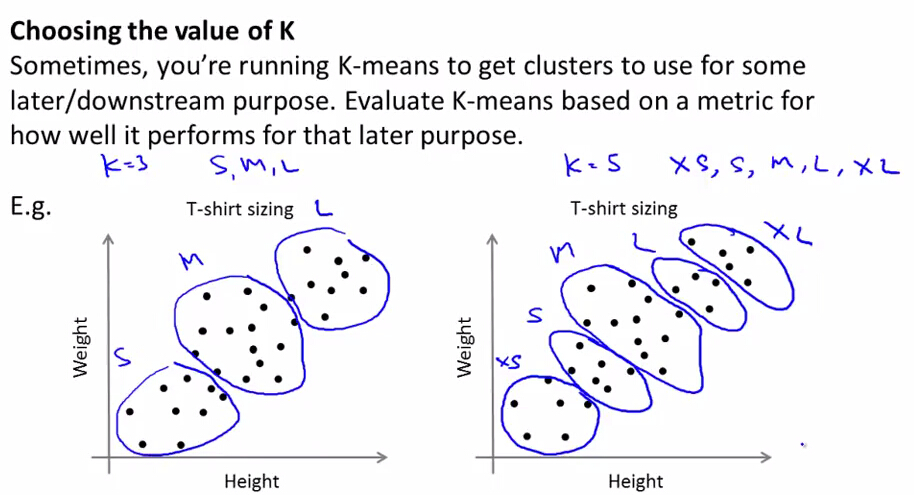
通过后续的一些目的，如市场方面的一些计算评估等。例如，T-shirt的例子，是将其设计为3种尺码还是5种尺码呢？要根据后续我们的一些目的来确定，是想T-shirt适应更多的顾客(5种)还是希望T-shirt更便宜(3种)，来确定K的值。

总结

  1. 选择K值现在大多数还是通过你的理解与洞察手动来选择的
  2. 可以尝试通过elbow method来选择K值，但是它并不通用，因为很多情况下，肘部点并不明确
  3. 大多数情况下，我们根据后续的目的来选择K值，看后续要做些什么，来看我们的K值应该怎么选

K-means:如何选择K(cluster的数目)的更多相关文章

  1. 9-n个人中选k个人的选择方法种类

    用递归法计算从n个人中选择k个人组成一个委员会的不同组合数分析: 1.如果k>n,结果为0 2.k=n时,只有1组 3.k<n的时候,可以把解空间分为两部分:假设其中一个人叫X,那么选X的 ...

  2. 【算法30】从数组中选择k组长度为m的子数组，要求其和最小

    原题链接:codeforce 267 Div2 C 问题描述: 给定长度为n的数组a[],从中选择k个长度为m的子数组,要求和最大. 形式描述为:选择$k$个子数组[$l_1$, $r_1$], [$ ...

  3. 第k大数（前k大数）

    题目:设计一组N个数,确定其中第k个最大值 1,普通方法(先排序,然后遍历,得到第k大的数)      注:如果是数组,直接arr[k],我们可以对这个乱序数组按照从大到小先行排序,然后取出前k大,总 ...

  4. 华为OJ2051-最小的K个数（Top K问题）

    一.题目描述 描述: 输入n个整数,输出其中最小的k个. 输入: 输入 n 和 k 输入一个整数数组 输出: 输出一个整数数组 样例输入: 5 2 1 3 5 7 2 样例输出: 1 2 二.Top ...

  5. 第K短路+严格第K短路

    所谓K短路,就是从s到t的第K短的路,第1短就是最短路. 如何求第K短呢?有一种简单的方法是广度优先搜索,记录t出队列的次数,当t第k次出队列时,就是第k短路了.但点数过大时,入队列的节点过多,时间和 ...

  6. [CareerCup] 13.1 Print Last K Lines 打印最后K行

    13.1 Write a method to print the last K lines of an input file using C++. 这道题让我们用C++来打印一个输入文本的最后K行,最 ...

  7. 一些简单的问题. 2的10次方与k (涉及到b k m的要用乘来解读)

    2的10次方是k k就表示2的10次方 2的16次方,解读为 2的6次方(64)*2的10次方(k)  简写为64k    64k=64*k 同理2的20次方  解读为2的10次方*2的10次方  k ...

  8. 机器学习 —— 基础整理（三）生成式模型的非参数方法： Parzen窗估计、k近邻估计；k近邻分类器

    本文简述了以下内容: (一)生成式模型的非参数方法 (二)Parzen窗估计 (三)k近邻估计 (四)k近邻分类器(k-nearest neighbor,kNN) (一)非参数方法(Non-param ...

  9. 快速排序／快速查找（第k个， 前k个问题）

    //快速排序:Partition分割函数,三数中值分割 bool g_bInvalidInput = false; int median3(int* data, int start, int end) ...

随机推荐

  1. Java之static作用的深度总结

    1.深度总结 引用一位网友的话,说的非常好,如果别人问你static的作用:如果你说静态修饰 类的属性 和 类的方法 别人认为你是合格的:如果是说 可以构成 静态代码块,那别人认为你还可以: 如果你说 ...

  2. 移动端实现裁剪图片生成base64图片(可缩放)

    移动端实现裁剪图片生成base64图片(可缩放)<pre><!DOCTYPE html><html lang="en"> <head> ...

  3. pat 1100

    1100 Mars Numbers (20 分)   People on Mars count their numbers with base 13: Zero on Earth is called ...

  4. 分页Model

    <?php namespace Admin\Model; use Think\Model; class PageModel extends Model{ /* *此函数分页函数.传入表名和当前页 ...

  5. php判断key是否存在的两种方法

    array_key_exists($key, $array) isset($array[$key]) 两种方式都可以!

  6. netty例子-客户端每隔5秒发送查询时间的请求，服务器端响应请求

    netty是jboss公司开发的,基于异步的.事件驱动的网络应用程序框架,快速开发高性能.高可靠性的服务器和客户端程序 public class TimeServer { ; public void ...

  7. 17 SpringMVC response响应

    1.Model.ModelMap和ModelAndView的使用详解 Spring-MVC在请求处理方法可出现和返回的参数类型中,最重要就是Model和ModelAndView了,对于MVC框架,控制 ...

  8. C++中STL中简单的Vector的实现

    该vector只能容纳标准库中string类, 直接上代码了,StrVec.h文件内容为: #ifndef STRVEC_H #define STRVEC_H #include<iostream ...

  9. LeetCode 5215. 黄金矿工（Java）DFS

    题目: 5215. 黄金矿工 你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为 m * n 的网格 grid 进行了标注.每个单元格中的整数就表示这一单元格中的黄金数量:如果该 ...

  10. QT5的QChart使用记录

    如果需要在QT中使用QChart类,需要在安装的时候勾选QChart选项,在工程的 .pro 文件里面添加 QT += charts 语句,包含 QChart 头文件就行了. 对于图表的显示,可以先拖 ...