linux centos7 防止暴力破解

系统 centos 7.4 系统，不知道的可以用 cat /etc/redhat-release 查看

利用到了linux 系统的日志，每次我们登陆服务器时，如果有登陆认证失败的情况，会在服务器的/var/log/secure文件中记录日志。错误日志如下截图：

 tail -3f /var/log/secure

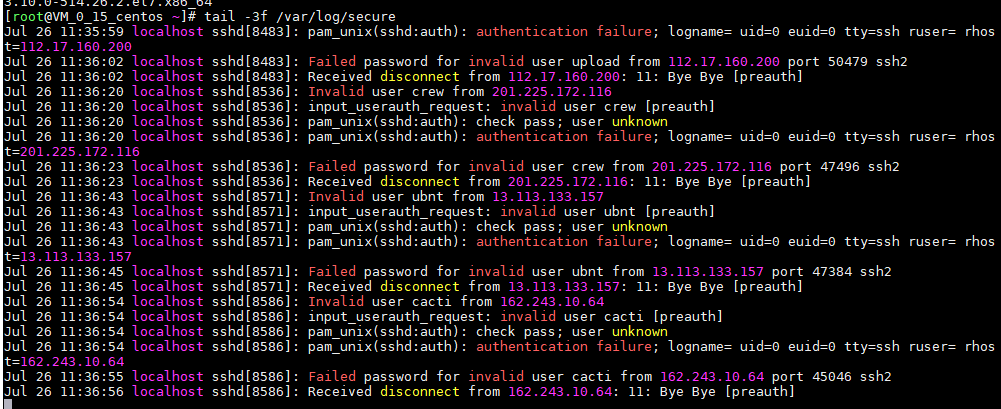
执行 du -h /var/log/secure 是否被暴力攻击超过1M基本说明被攻击

du -h /var/log/secure

什么是暴力破解，简单来说就是对一个服务器进行无数次尝试登陆，并用不同的密码进行登陆直到可以登陆成功。暴力破解的基本步骤可以分为以下几步：　　　　　　

　　　　　　1. 找到对应的linux服务器 Ip地址

　　　　　　2.扫描端口号：22 nmap扫描端口

　　　　　　3.开始暴力破解 : 一般root 破解你的密码登录你的机器破坏盗取你的重要的数据

　　对于这种情况我们有以下5种解决办法：

将密码设置复杂，长度大于8位或者最好大于20位，密码的复杂度：由大小写字母以及字符和数字组成。 0-9 a-z A-Z @!#$%*. 等等。
更改端口号，默认的端口是sshd(22),修改默认端口号。
不用root用户登陆(禁止root用户登陆)，使用其他用户登陆并且拥有root用户权限。
sshd服务，直接编写脚本检查/var/log/secure 内登录失败次数超过某个阈值的ip并将它添加到/etc/hosts.deny（使用fail2ban的优点更多）
使用fail2ban,起到登录失败多次后直接禁止某个时间段此ip登陆。

yum安装fail2ban方法参考：https://www.cnblogs.com/operationhome/p/9184580.html

以下是使用onestack软件安装fail2ban防止暴力破解方法：

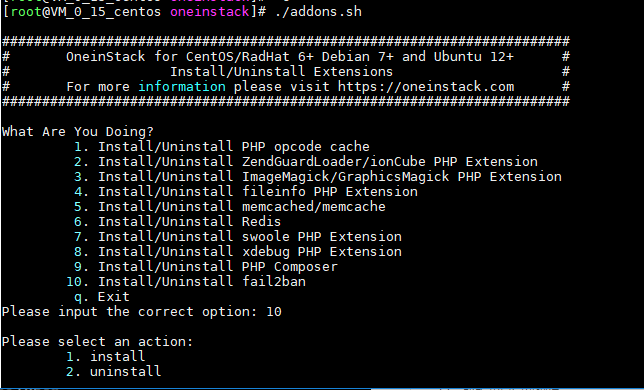
使用《OneinStack》，内置fail2ban，切换到OneinStack安装目录运行./addons.sh命令，然后选择10，再选择1安装即可，安装完成自动启动

Fail2ban配置文件说明

vim /etc/fail2ban/jail.d/jail.local

#defalut这里是设定全局设置，如果下面的监控没有设置就以全局设置的值设置。

[DEFAULT]

# 用于指定哪些地址ip可以忽略 fail2ban 防御,以空格间隔。

ignoreip = 127.0.0.1/

# 客户端主机被禁止的时长（默认单位为秒）

bantime  =

# 过滤的时长（秒）

findtime  =

# 匹配到的阈值（次数）

maxretry = 

[ssh-iptables]

# 是否开启

enabled  = true

# 过滤规则

filter   = sshd

# 动作

action   = iptables[name=SSH, port=, protocol=tcp]

# 日志文件的路径

logpath  = /var/log/secure

# 匹配到的阈值（次数）

maxretry =

注意：action，port=22，如果我们更改了sshd服务的端口号，我能需要在这里设置对应的端口号，否则配置不生效。

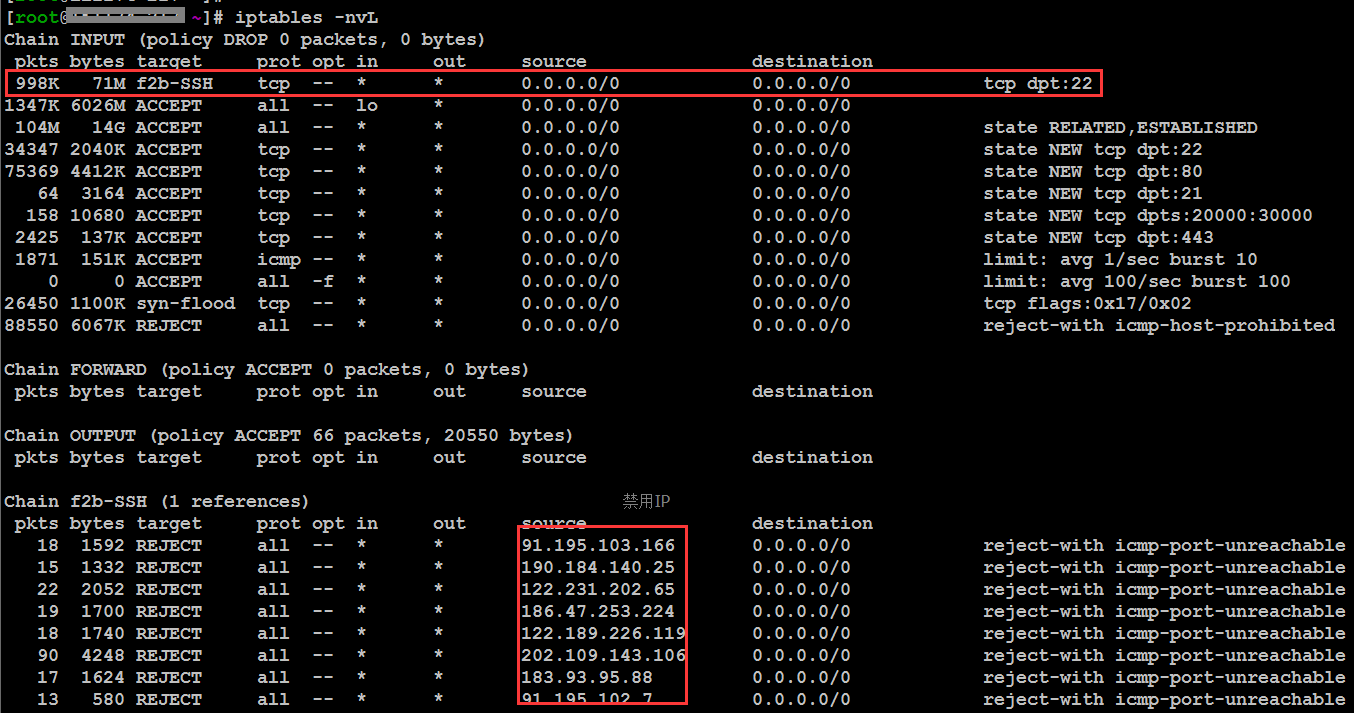
fail2ban会自动禁止在最近10分钟内有超过5次访问尝试失败的任意IP地址。这个IP地址将会在24小时内一直被禁止访问SSH服务。安装设置启用后，Fail2ban会在iptables添加相关规则，如下：

查看fail2ban日志

tailf /var/log/fail2ban.log

查看fail2ban状态

/usr/local/python/bin/fail2ban-client status ssh-iptables

红框的是显示出被禁止IP地址列表

fail2ban解锁IP

/usr/local/python/bin/fail2ban-client set ssh-iptables unbanip 91.195.103.166