Organising the Organisation(uva10766)(生成树计数)

Input

Output

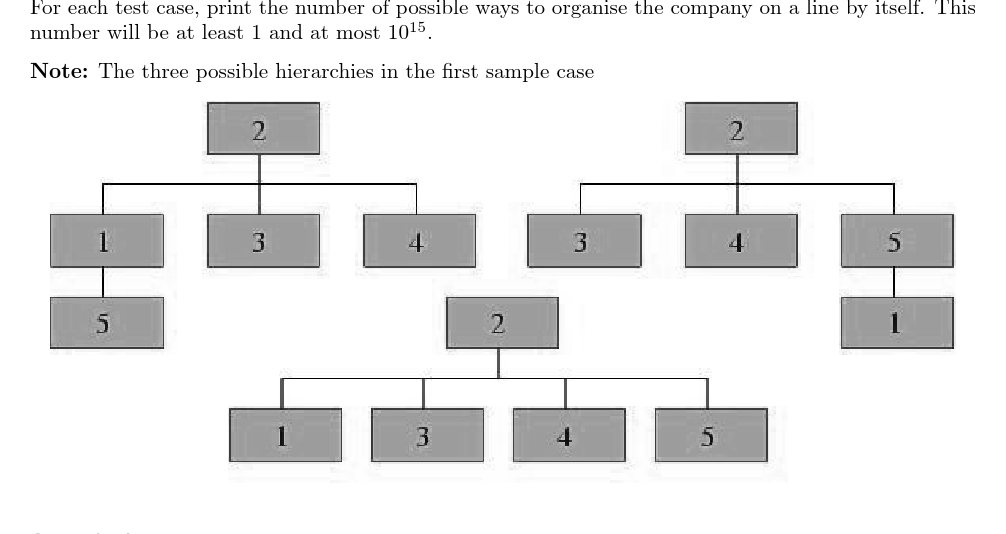
Sample Input

5 5 2
3 1
3 4
4 5
1 4
5 3
4 1 1
1 4
3 0 2

Sample Output

3
8
3

题意：

有一张图上有\(n\)个点，两两之间有一条边，现在切断\(m\)条边，求剩下的图中有多少种不同的生成树。

题解：

生成树计数

做这道题，需要三个预备知识：

\(Kirchhoff\)矩阵

首先先构造两个矩阵

度数矩阵D：是一个\(N×N\)的矩阵，其中

\(D[i][j]=0(i≠j)\)，\(D[i][i]=i\)号点的度数

邻接矩阵A：是一个\(N×N\)的矩阵，其中

\(A[i][i]=0,A[i][j]=A[j][i]=i\),\(j\)之间的边数

然后\(Kirchhoff\)矩阵\(K=D-A\)

举个例子，对于如下的无向图，三个矩阵分别为：（图片来源于网络）

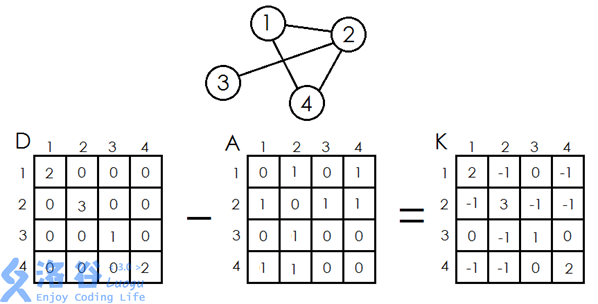
行列式\(det(K)\)及其求法

考虑对于原矩阵\(K\)，我们可以得到其行列式的求和式：

\(\det(A) = \sum_{\sigma \in S_n} sgn(\sigma) \prod_{i=1}^n a_{i,\sigma(i)}\)

其中\(S_n\)是指全排列的集合,\(\sigma\)就是一个全排列,如果\(\sigma\)的逆序对对数为偶数,则\(sgn(\sigma)=1\)否则\(=-1\)

然后我们可以用\(n!\)左右的算法解决了，但这绝对会TLE啊！！！

让我们来研究一下行列式的性质（我就列了几条有用的）:

• 性质.1 互换矩阵的两行(列)，行列式变号。
• 性质.2 如果该矩阵为一三角形矩阵。则该矩阵的行列式等于A的对角元素的乘积。
• 性质.3 如果把矩阵的某一行(列)加上另一行(列)的k倍，则行列式的值不变。
• 性质.4 如果矩阵有两行(列)成比例(比例系数k)，则行列式的值为0。
• 性质.5 互换矩阵的两行(列)，行列式变号。

结合这几个性质，我们可以很明显的看出可以用高斯消元优化了，复杂度为\(O(n^3)\)。

\(Matrix-Tree\)定理:

• 对于一个无向图G，它的生成树个数等于其\(Kirchhoff\)矩阵任何一个n-1阶主子式的行列式的绝对值。

好吧其实我没看懂这个定理，但经过一番感性理解，大概就是这个意思：

• 我们把\(Kirchhoff\)矩阵的第\(i\)行和第\(i\)列去掉，剩下矩阵的行列式的绝对值就是生成树的数量。

其中\(i\)为\(1\)~\(n\)中任意一个数(真的是任意一个就可以了)，为了方便这题我们直接设它为n就行了。

---

有了这几个预备知识后，这一题就可以做了。

上代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll A[60][60],K[60][60];
ll tree_sum(int n){
    ll ret=1;
    for(int i=1;i<=n;++i){
        if(!K[i][i]){
            bool b=0;
            for(int j=i+1;j<=n;++j){
                if(K[j][i]){
                    b=1;
                    for(int k=1;k<n;++k){
                        swap(K[i][k],K[j][k]);
                    }ret=-ret;
                    break;
                }
            }
            if(!b)return 0;
        }
        for(int j=i+1;j<=n;++j){
            while(K[j][i]){
                ll t=K[i][i]/K[j][i];
                for(int k=i;k<=n;++k){
                    K[i][k]-=t*K[j][k];
                    swap(K[i][k],K[j][k]);
                }
                ret=-ret;
            }
        }ret*=K[i][i];
    }return ret;
}
int main(){
    int n,m,k;
    while(~scanf("%d%d%d",&n,&m,&k)){
        memset(A,0,sizeof A);
        memset(K,0,sizeof K);
        for(int i=1;i<=m;++i){
            int x,y;
            scanf("%d%d",&x,&y);
            A[x][y]=A[y][x]=1;
        }
        for(int i=1;i<=n;++i){
            for(int j=1;j<=n;++j){
                if(i!=j&&!A[i][j]){
                    K[i][i]++;
                    K[i][j]--;
                }
            }
        }--n;
        ll ans=tree_sum(n);
        printf("%lld\n",ans);
    }
}