noVNC连接CentOS，以Web方式交付VNC远程连接

什么是noVNC？

• noVNC 是一个 HTML5 VNC 客户端，采用 HTML 5 WebSockets, Canvas 和 JavaScript 实现，noVNC 被普遍用在各大云计算、虚拟机控制面板中，比如 OpenStack Dashboard 和 OpenNebula Sunstone 都用的是 noVNC。

• noVNC 采用 WebSockets 实现，但是目前大多数 VNC 服务器都不支持 WebSockets，所以 noVNC 是不能直接连接 VNC 服务器的，需要一个代理来做 WebSockets 和 TCP sockets 之间的转换。这个代理在 noVNC 的目录里，叫做 websockify 。

实验环境

• 操作系统：CentOS 6.6

• IP： 192.168.204.128

一、修改网络配置

1）关闭防护墙

1 2	setenforce 0 service iptables stop

2）查看本机IP地址

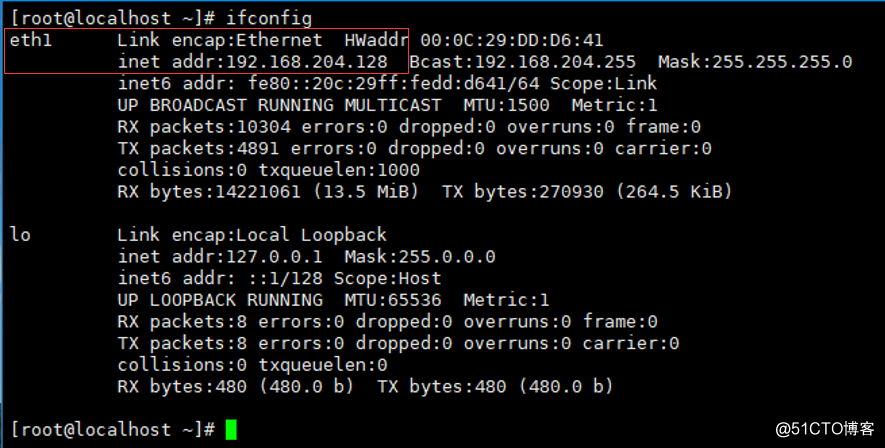
二、安装 git

 

1	yum install git -y

三、安装配置 tigervnc

 

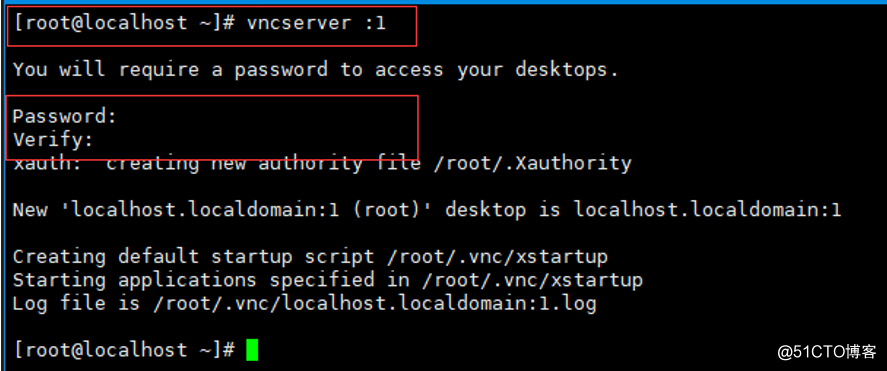
1 2	yum install tigervnc-server vncserver :1

安装 tigervnc-server 过程：

输入 vncserver :1 启动服务，并输入密码（注意密码长度不小于6位）。

四、安装 noVNC

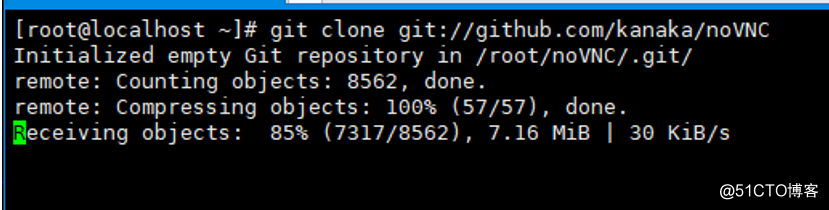
1）下载 noVNC

1	git clone git://github.com/kanaka/noVNC

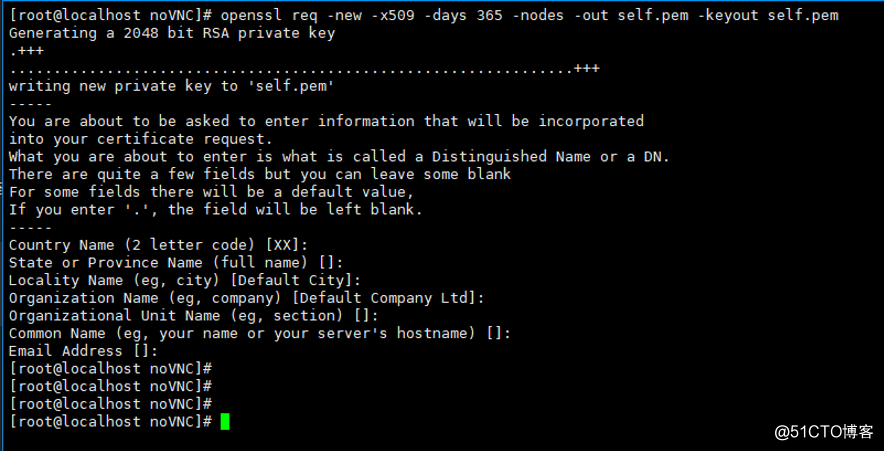
2）创建安全连接

^注：  VNC的默认会话不是安全的，需要创建一个安全的VNC连接。创建完毕的证书 `self.pem` 需要放置到 `noVNC/utils` 目录下，当启动 noVNC 时，websockify将自动装载证书。

1 2	cd ./noVNC/utils/ openssl req -new -x509 -days 365 -nodes -out self.pem -keyout self.pem

一路回车下去 ... ...

3）运行 noVNC

1 2	# 在noVNC目录下，执行 ./utils/launch.sh --vnc localhost:5901

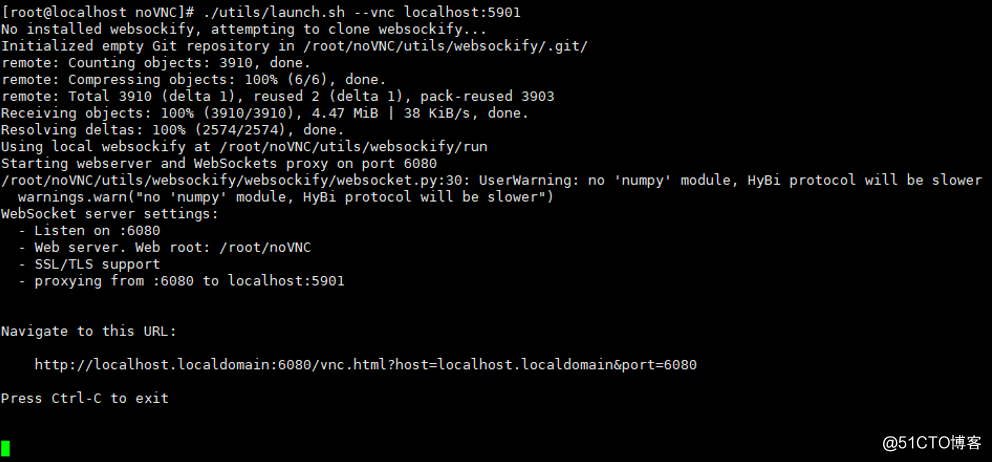
五、测试连接

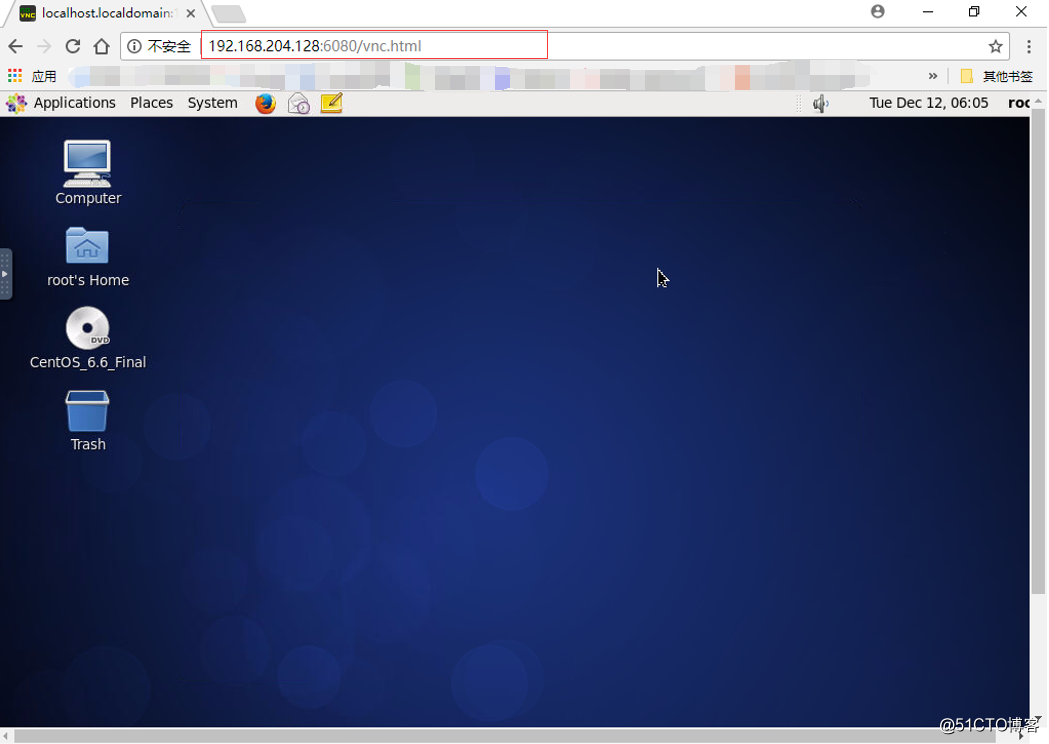
在浏览器访问（注意替换成自己的IP地址） http://192.168.204.128:6080/vnc.html

输入密码，连接成功！

六、安装脚本

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

#!/bin/bash     # stop selinux and iptables setenforce 0 service iptables stop     # install vncserver and git yum install tigervnc-server git -y vncserver :1 # 此时会提示输入密码     # download noVNC git clone git://github.com/kanaka/noVNC     # create secure connection cd ./noVNC/utils/ openssl req -new -x509 -days 365 -nodes -out self.pem -keyout self.pem     # run noVNC cd ../ ./utils/launch.sh --vnc localhost:5901     # running