CodeForces - 707C

C. Pythagorean Triples

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

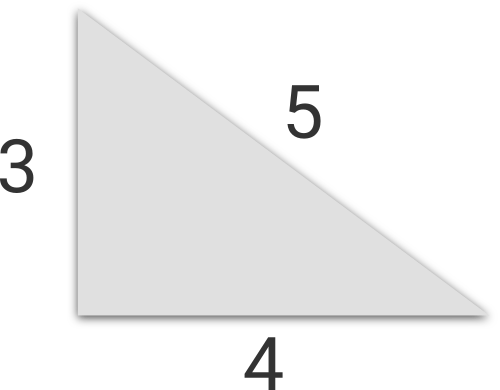
Katya studies in a fifth grade. Recently her class studied right triangles and the Pythagorean theorem. It appeared, that there are triples of positive integers such that you can construct a right triangle with segments of lengths corresponding to triple. Such triples are called Pythagorean triples.

For example, triples (3, 4, 5), (5, 12, 13) and (6, 8, 10) are Pythagorean triples.

Here Katya wondered if she can specify the length of some side of right triangle and find any Pythagorean triple corresponding to such length? Note that the side which length is specified can be a cathetus as well as hypotenuse.

Katya had no problems with completing this task. Will you do the same?

Input

The only line of the input contains single integer n (1 ≤ n ≤ 109) — the length of some side of a right triangle.

Output

Print two integers m and k (1 ≤ m, k ≤ 1018), such that n, m and k form a Pythagorean triple, in the only line.

In case if there is no any Pythagorean triple containing integer n, print  - 1 in the only line. If there are many answers, print any of them.

Examples

input

Copy

3

output

4 5

input

Copy

6

output

8 10

input

Copy

1

output

-1

input

Copy

17

output

144 145

input

Copy

67

output

2244 2245

Note

思路：

直接跑表：

#include<bits/stdc++.h>
using namespace std;

int main()
{
    for(int i = ;i <= ;i ++){
        for(int j = ;j <= ;j++){
            for(int k = j;k <= ;k ++){
                if(i*i==j*j+k*k||i*i==j*j-k*k||i*i==k*k-j*j){
                    cout<<i<<" "<<j<<" "<<k<<endl;
                }
            }
        }
    }
}

跑出：

由上面的代码可以看出：

如：

3 4 5

4 3 5

5 12 13

6 8 10

奇数都存在一对只相差1的两边，偶数都存在一条相差为2的两边。

然后脑补了一下规律：

偶数为： n*n/4 -1, n*n/4+1

奇数为： n*(n+1)/2 , n*(n+1)+1

然后就过了。。。

实现代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main()
{
    ll n;
    cin>>n;
    if(n <= )
        cout<<-<<endl;
    else if((n/)*==n){
        cout<<n*n/-<<" "<<n*n/+<<endl;
    }
    else{
        cout<<(n/)*(n+)<<" "<<(n/)*(n+)+<<endl;
    }
}