[ML学习笔记] XGBoost算法

[ML学习笔记] XGBoost算法

回归树

决策树可用于分类和回归，分类的结果是离散值（类别），回归的结果是连续值（数值），但本质都是特征（feature）到结果/标签（label）之间的映射。

这时候就没法用信息增益、信息增益率、基尼系数来判定树的节点分裂了，那么回归树采用新的方式是预测误差，常用的有均方误差、对数误差等（损失函数）。而且节点不再是类别，而是数值（预测值），划分到叶子后的节点预测值有不同的计算方法，有的是节点内样本均值，有的是最优化算出来的比如Xgboost。

XGBoost算法

XGBoost是由许多CART回归树集成。区别于随机森林的bagging集成，它是一种boosting集成学习（由多个相关联的决策树联合决策，下一棵决策树输入样本会与前面决策树的训练和预测相关）。它的目标是希望建立K个回归树，使得树群的预测值尽量接近真实值（准确率）而且有尽量大的泛化能力（寻求更为本质的东西）。

记w为叶子节点的权值，x为分类结果，则最终预测值 \(\hat{y}_i = \sum_j w_j x_{ij}\)。

设目标函数为 \(l(y_i,\hat{y}_i)=(y_i-\hat{y}_i)^2\)。

对于一组数值需要求平均，相当于求其期望 \(F^*(\overrightarrow{x})=argminE_{(x,y)}[L(y,F(\overrightarrow{x}))]\)

最终结果由多个弱分类器组成，集成的结果：\(\hat{y}_i = \sum_{k=1}^K f_k(x_i), \quad f_k\in F\)

XGBoost本质是提升树，也即每加一棵效果更好（目标函数更优）

定义正则化惩罚项 \(\Omega(f_t)=\gamma T+\frac{1}{2}\lambda \sum_{j=1}^T \omega_j^2\)（叶子个数 + w的L2正则项）

如何选择每一轮加入什么f（预测值->落入的叶子权值）：选取使得目标函数尽量最大地降低（找到\(f_t\)来优化这一目标）

\[
\begin{split}
Obj^{(t)}&=\sum_{i=1}^n l(y_i,\hat{y}_i^{(t)})+\sum_{i=1}^n\Omega(f_i)\\
&=\sum_{i=1}^n l(y_i,\hat{y}_i^{(t-1)}+f_t(x_i))+ \Omega(f_t)+constant\\
&=\sum_{i=1}^n (y_i-(\hat{y}_i^{(t-1)}+f_t(x_i))^2+ \Omega(f_t)+constant\\
&=\sum_{i=1}^n [2(\hat{y}_i^{(t-1)}-y_i)f_t(x_i)+f_t(x_i)^2]+ \Omega(f_t)+constant\\
\end{split}
\]

用\(\hat{y}_i^{(t-1)}-y_i\) 描述前t-1棵的总预测值与真实值之间的差异（残差），因此梯度提升决策树也称残差决策树。

目标函数Obj是一个队树结构进行打分的函数（结构分数 structure score），分数越小代表树结构越好。用泰勒展开近似求解：

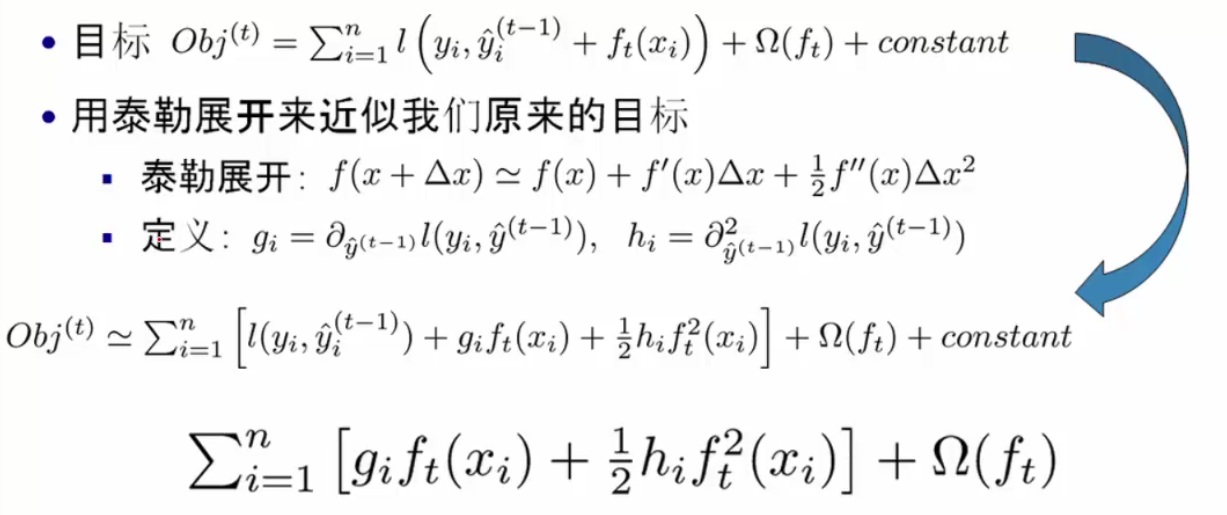
由对样本的遍历变换为对叶节点的遍历

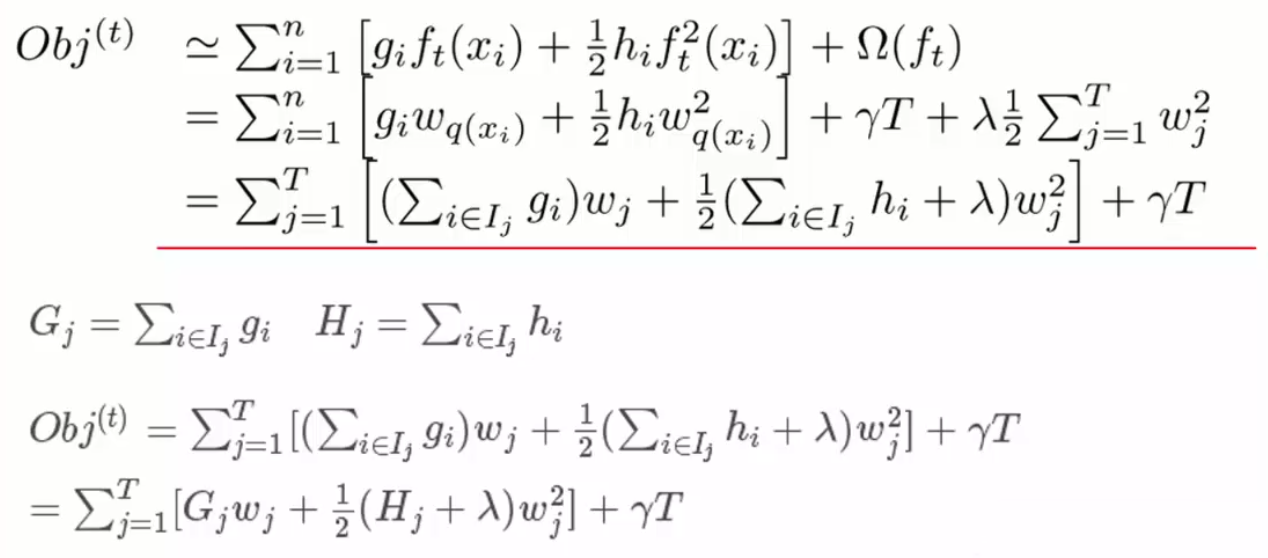
单节点怎么切分（分叉）：枚举所有可能的分割方案，假设要枚举所有x<a这样的条件，对于某个特性的分割a，分别计算切割前和分割后的差值以求增益。

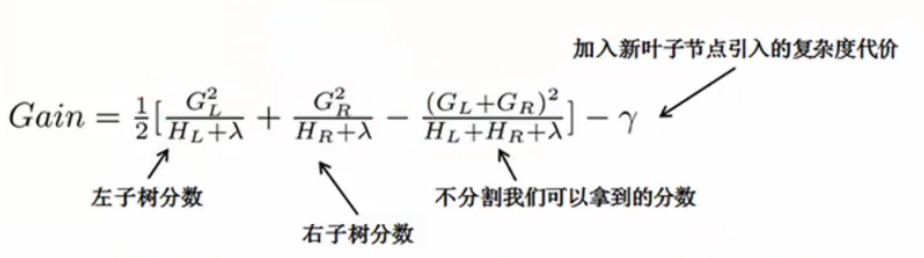
推荐阅读：

• 陈天奇博士的文章 Introduction to Boosted Trees （附：原PPT地址、中文笔记博客）