LeetCode题解之Pascal's Triangle II

1、题目描述

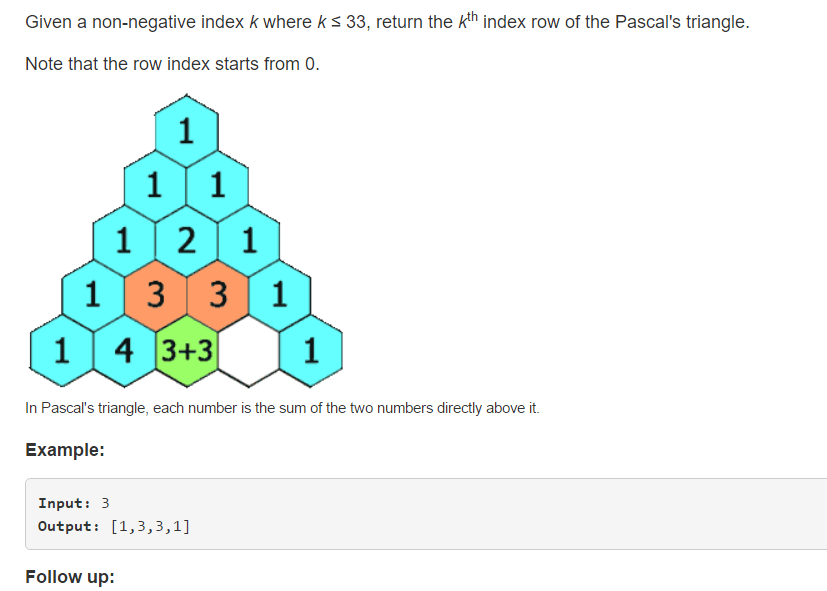
2、题目分析

题目要求返回杨辉三角的某一行，需要将杨辉三角的某行的全部计算出来。

3、代码实现

  vector<int> getRow(int rowIndex) {

         if( rowIndex ==  )
             return vector<int>(,);

         vector<int>b{,};
         int n = ;
         while(n <= rowIndex){
             vector<int> r = calNextline(b);
             b.resize( r.size() );
             for(int i = ; i < r.size(); i++){
                 b[i] = r[i];
             }
             n++;
         }

         return b;
     }

     vector<int> calNextline( vector<int> v){
         if( v.size() < ){
             return v;
         }

         vector<int> rv(v.size() + , );

         for(int i = ; i < v.size()-; i++){
             rv[i+] = v[i] + v[i+];
         }
         return rv;
     }