《机器学习实战》ID3算法实现

---

注释：之前从未接触过决策树，直接上手对着书看源码，有点难，确实有点难～～

　　　本代码是基于ID3编写，之后的ID4.5和CART等还没学习到

一.决策树的原理

　　没有看网上原理，直接看源码懂得原理，下面是我一个抛砖引玉的例子：

　　　　　

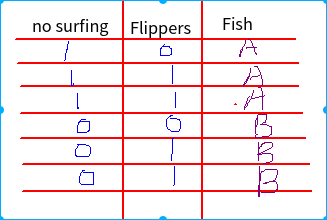
　　太丑了，在Linux下面操作实在不习惯，用的Kolourpqint画板也不好用，凑合看吧！

　　假设有两个特征：no surfing 、Flippers ，一个结果：Fish

　　现在假如给你一个测试：no surfing = 1, Flippers=0, 如何知道Fish的结果？太简单了Fish==A...

　　现在样本你不知道排序的情况下，那我们操作的步骤只能是两种：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1.no surfing = 1时判断Fish，直接得出结果Fish==A

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2.Flippers=0时判断Fish，Fish可能是A也可能是B，再判断no surfing =1时，得出Fish == A

　　从上面我们可以看出，你选择的特征顺序对结果无影响，但是对计算的过程影响很大，我们能不能找到一种很好的途径去解决这个问题呢？

　　下面是两种方法：

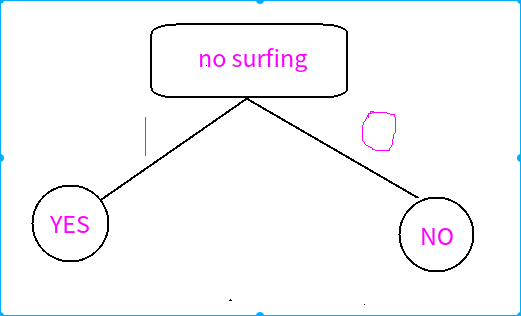
方法一

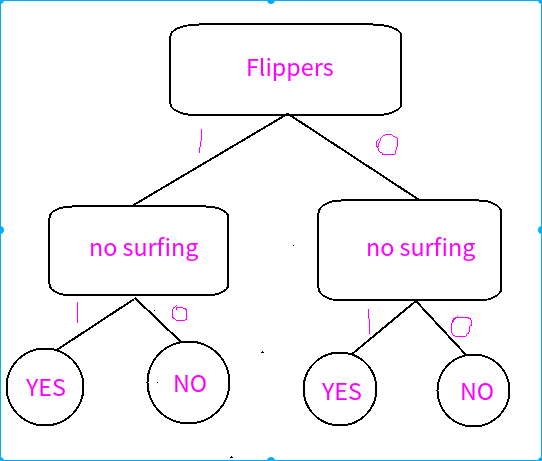
方法二

　　由以上的两种思路可以得出，不同的分类方法差距很大吧？

　　决策树就是用来解决如何选用最佳的方法的一种算法！！！

　　一点不了解的，先花几分钟看一下我“信息熵”，这是整个算法的核心。

 

二.决策树的实现

　　（1）计算信息熵

　　　　　　为什么计算“信息熵”？自己去看原理就懂了。

 def claShannonEnt(setData):
      lengthData = len(setData)
      dicData = {}
      for cnt in range(lengthData):
           if setData[cnt,-1] not in dicData.keys():
                dicData[setData[cnt,-1]] = 0
           dicData[setData[cnt,-1]] += 1
      Hent = 0.0#输出信息ent
      for key in dicData.keys():
           pData = float(dicData[key])/lengthData
           Hent -= pData*math.log(pData,2)
      return Hent

　　（2）划分数据集

　　　　　　划分之后计算部分的信息熵之和，信息熵越小越好，信息增益越大越好。

 def splitData(setData,axis,value):
      '''  setData: sample sata
           axis   : 轴的位置
           value  : 满足条件的值
      '''
      lengthData = setData.shape[0]
      resultMat = np.zeros([1,setData.shape[1]])
      for count in range(lengthData):
           if int(setData[count,axis]) == int(value) :
                resultMat = np.vstack((resultMat,setData[count,:]))
      returnMat = resultMat[1:,:]
      resultMat = np.hstack((returnMat[:,0:axis],returnMat[:,axis+1:]))
      return resultMat

　　（3）选择最佳的划分方案

　　　　　　这里的原理就是划分之后的信息熵变小，信息增益变大，其中信息熵越小越好，也就是信息增益越大越好，循环比较每种划分之后的信息增益。

 def chooseBestTeature(setData):
      numFeature = setData.shape[1] - 1  #特征数量
      baceEntropy = claShannonEnt(setData)    #信息熵
      bestGain = 0.0 #最好增益
      bestFeature = 0    #最好特征
      for i in range(numFeature):
           #featList = [example[i] for example in setData]
           featList = setData[:,i]
           uniquaVals = set(featList)    #不同的Value值,set之后就变成无序集合
           newEntropy = 0.0
           for value in uniquaVals:
                subDataSet = splitData(setData,i,value)#分割特征
                prob = len(subDataSet)/float(len(setData))
                newEntropy += prob * claShannonEnt(subDataSet)#平均信息熵
           infoGain = baceEntropy - newEntropy
           if (infoGain > bestGain):#求得最大增益
                bestGain = infoGain
                bestFeature = i
      return bestFeature

　　（4）计算分类之后的标签

　　　　　　这里有点难理解，准备在下面程序讲解的，写到这里就直接讲解了。

　　　　　　这是为了分类不了的情况做的准备，比如：[1,1,'yes'],[1,1,'no'],[1,0,'no'],[1,0,'yes'],[0,0,'no'],[0,0,'yes'],[0,1,'no'],[0,1,'yes']，大家可以按照上面的方法动手试试怎么分割？

　　　　　　我们可以想象一下，就像以前中学学的解方程，Y₁+Y₂=10 && 2Y₁ +2Y₂ =10 ，你怎么求解Y₁和Y₂ ？两个有冲突的方程和上面的样本之间的冲突是一样的。

　　　　　　这明显是一个出错的样本导致的，那怎么解决呢？

　　　　　　再给出一组样本：[1,1,'yes'],[1,1,'yes'],[1,1,'no'],[1,1,'yes']，我们利用错误的样本为少数，多数的样本为正确的，所以[1,1] = 'YES'

 #计算分类之后的标签
 def majorityCnt(classList):
      classCount = {}
      for vote in classList:
           if vote not in classCount.keys():
                classCount[vote] = 0
           classCount[vote] += 1
      sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
      return sortedClassCount

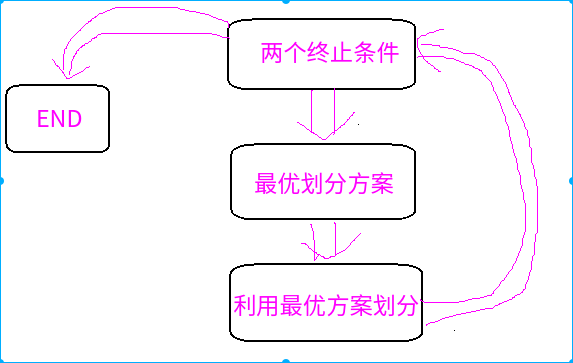
　　（5）建立决策树

　　　　　　这里采用递归的方法进行划分

　　　　　　调出循环的条件是：

　　　　　　　　　　　　　　　　1.最后的标签相同--->>>也就是最后就省一个答案了，没必要划分直接得出结果了。

　　　　　　　　　　　　　　　　2.就是第四点说的无解题，那就多的保留，少的丢弃。

 def creatTree(dataSet,labels):
      classList = dataSet[:,-1]
      #标签全部相等的时候退出
      if list(classList).count(classList[0]) == len(list(classList)):
           return classList[0]
      #最后的标签不相同,这个时候没办法分割，所以只能选择一个占比例大的标签了，博客会给具体例子
      if len(dataSet[0,:]) == 1:
           return majorityCnt(classList)
      bestFeat = chooseBestTeature(dataSet)
      bestFeatLabel = labels[bestFeat]
      myTree = {bestFeatLabel:{}}
      del(labels[bestFeat])
      featValue = dataSet[:,bestFeat]
      uniqueVals = set(featValue)
      for value in uniqueVals:
           subLabels = labels[:]
           myTree[bestFeatLabel][value] = creatTree(splitData(dataSet,bestFeat,value),subLabels)
      return myTree

　　　

　　 （6）使用决策树

　　　　　　就像建立决策树一样，采用递归一层一层的去找到数据属于哪个类，看懂上面的建立之后现在这里不很简单

 def classify(inputTrees,featLabels,testVec):
      firstStr = list(inputTrees.keys())[0]#字典首元素
      secondDict = inputTrees[firstStr]#下一个字典
      featIndex = featLabels.index(firstStr)#标签中的位置
      for key in secondDict.keys():
           if testVec[featIndex] == int(key):#分支
                if type(secondDict[key]).__name__=='dict':#如果还是字典说明还得划分
                     classLabels = classify(secondDict[key],featLabels,testVec)#迭代划分
                else: classLabels = secondDict[key]#不是字典说明已经分类
      return classLabels

　　   （7）存储决策树函数

　　（8）总程序设计

　　　　　　注意：我用的是Numpy数据，而不是List数据，这是有区别的，没有完全按照书上编写！

 import numpy as np
 import matplotlib.pyplot as ply
 import math
 import operator
 
 def claShannonEnt(setData):
      lengthData = len(setData)
      dicData = {}
      for cnt in range(lengthData):
           if setData[cnt,-1] not in dicData.keys():
                dicData[setData[cnt,-1]] = 0
           dicData[setData[cnt,-1]] += 1
      Hent = 0.0#输出信息ent
      for key in dicData.keys():
           pData = float(dicData[key])/lengthData
           Hent -= pData*math.log(pData,2)
      return Hent
 
 def splitData(setData,axis,value):
      '''  setData: sample sata
           axis   : 轴的位置
           value  : 满足条件的值
      '''
      lengthData = setData.shape[0]
      resultMat = np.zeros([1,setData.shape[1]])
      for count in range(lengthData):
           if int(setData[count,axis]) == int(value) :
                resultMat = np.vstack((resultMat,setData[count,:]))
      returnMat = resultMat[1:,:]
      resultMat = np.hstack((returnMat[:,0:axis],returnMat[:,axis+1:]))
      return resultMat
 
 def chooseBestTeature(setData):
      numFeature = setData.shape[1] - 1  #特征数量
      baceEntropy = claShannonEnt(setData)    #信息熵
      bestGain = 0.0 #最好增益
      bestFeature = 0    #最好特征
      for i in range(numFeature):
           #featList = [example[i] for example in setData]
           featList = setData[:,i]
           uniquaVals = set(featList)    #不同的Value值,set之后就变成无序集合
           newEntropy = 0.0
           for value in uniquaVals:
                subDataSet = splitData(setData,i,value)#分割特征
                prob = len(subDataSet)/float(len(setData))
                newEntropy += prob * claShannonEnt(subDataSet)#平均信息熵
           infoGain = baceEntropy - newEntropy
           if (infoGain > bestGain):#求得最大增益
                bestGain = infoGain
                bestFeature = i
      return bestFeature
 
 #计算分类之后的标签
 def majorityCnt(classList):
      classCount = {}
      for vote in classList:
           if vote not in classCount.keys():
                classCount[vote] = 0
           classCount[vote] += 1
      sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
      return sortedClassCount
 
 def creatTree(dataSet,labels):
      classList = dataSet[:,-1]
      #标签全部相等的时候退出
      if list(classList).count(classList[0]) == len(list(classList)):
           return classList[0]
      #最后的标签不相同,这个时候没办法分割，所以只能选择一个占比例大的标签了，博客会给具体例子
      if len(dataSet[0,:]) == 1:
           return majorityCnt(classList)
      bestFeat = chooseBestTeature(dataSet)
      bestFeatLabel = labels[bestFeat]
      myTree = {bestFeatLabel:{}}
      del(labels[bestFeat])
      featValue = dataSet[:,bestFeat]
      uniqueVals = set(featValue)
      for value in uniqueVals:
           subLabels = labels[:]
           myTree[bestFeatLabel][value] = creatTree(splitData(dataSet,bestFeat,value),subLabels)
      return myTree

 import numpy as np
 import trees
 
 if __name__ == '__main__':
     testData = np.array([[1,1,'yes'],[1,1,'no'],[1,0,'no'],[1,0,'yes'],[0,0,'no'],[0,0,'yes'],[0,1,'no'],[0,1,'yes']])
     myTree = trees.creatTree(testData,['no surfacing','flippers'])#['yes','yes','no','no','no']
     print(myTree)