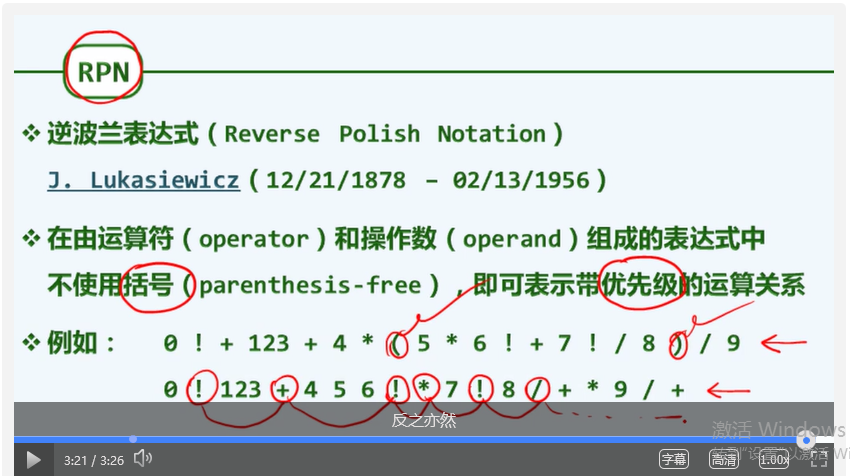
第四章 栈与队列(c5)栈应用:逆波兰表达式


第四章 栈与队列(c5)栈应用:逆波兰表达式的更多相关文章
- 逆波兰表达式[栈 C 语言 实现]
逆波兰表达式 逆波兰表达式又叫做后缀表达式.在通常的表达式中,二元运算符总是置于与之相关的两个运算对象之间,这种表示法也称为中缀表示.波兰逻辑学家J.Lukasiewicz于1929年提出了另一种表示 ...
- LeetCode150_Evaluate Reverse Polish Notation评估逆波兰表达式(栈相关问题)
题目: Evaluate the value of an arithmetic expression in Reverse Polish Notation. Valid operators are+, ...
- 关于利用STL栈求解四则中缀表达式以及中缀表达式转逆波兰表达式和逆波兰表达式的求解
今天总结一下栈的一个重要应用---四则数学表达式的求解 数学表达式的求解是栈的一个重要的应用,在计算机的应用中 如果求解一个四则运算表达式,我们可能会直接写一个程序例如什么printf("% ...
- ACM YTU 十进制与八进制的转换 (栈和队列) STL栈调用
十进制与八进制的转换(栈和队列) Description 对于输入的任意一个非负十进制整数,利用栈打印输出与其等值的八进制数. Input 111 Output 157 Sample Input 14 ...
- (5)剑指Offer之栈变队列和栈的压入、弹出序列
一 用两个栈实现队列 题目描述: 用两个栈来实现一个队列,完成队列的Push和Pop操作. 队列中的元素为int类型. 问题分析: 先来回顾一下栈和队列的基本特点: 栈:后进先出(LIFO) 队列: ...
- 中缀转逆波兰表达式 c++ 队列,栈
记得早在几十天以前,xty 学长曾让我学这个.一直推到了现在哈 咕咕咕(能鸽善鹉orz) 抱歉,学妹我来还愿了! 中缀表达式比较适合人类的计算,但是后缀表达式更适合机器计算(毕竟没有那么多运算符优先级 ...
- 第四章 Activity和Activity调用栈分析 系统信息与安全机制 性能优化
1.Activity生命周期理解生命周期就是两张图:第一张图是回字型的生命周期图第二张图是金字塔型的生命周期图 注意点(1)从stopped状态重新回到前台状态的时候会先调用onRestart方法,然 ...
- 剑指Offer 5. 用两个栈实现队列 (栈)
题目描述 用两个栈来实现一个队列,完成队列的Push和Pop操作. 队列中的元素为int类型. 题目地址 https://www.nowcoder.com/practice/54275ddae22f4 ...
- 第三十四章 POSIX消息队列
POSIX消息队列相关函数 mq_open 功能: 用来创建和访问一个消息队列 原型: mqd_t mq_open(const char *name, int oflag); //只能用来打开消息队列 ...
随机推荐
- 【4-1】js函数、事件、补充知识
一.函数操作 (一)字符串操作: (1)变量名.toLowerCase():--转小写 toUpperCase():----转大写 (2)变量名.substring(索引,截取到位数);--- ...
- spark 数据读取与保存
spark支持的常见文件格式如下: 文本,json,CSV,SequenceFiles,Protocol buffers,对象文件 1.文本 只需要使用文件路径作为参数调用SparkContext 中 ...
- idea 关闭代码自动折叠,形参提示,行数栏图标,启动不默认打开上次的项目
1,代码自动折叠 1.1,File > setting > Editor > General > Code Folding 1.2,勾选右侧不想要折叠的代码部分 2,形参提示 ...
- 关于存session,cookie还是数据库或者memcache的优劣,部分网上抄录
从效率考虑:cookie > memcache > 数据库cookie对服务器端负载没影响,如果加密.解密会多消耗一点点cpu.带宽倒是会消耗得多一点,同域名下的所有http reques ...
- mac 管理员权限变成了普通权限处理方法
在更换账户名称的时候出了这个问题.设置的时候不会显示用户名,没有电脑的管理权限了,找到如下方法解决的,试了可行. http://blog.csdn.net/vickylizy/article/deta ...
- day31-软件开发规范
一.为什么要规范软件开发? 1.1 为什么要有规范软件开发 你现在包括之前写的一些程序,所谓的'项目',都是在一个py文件下完成的,代码量撑死也就几百行,你认为没问题,挺好.但是真正的后端开发的项目, ...
- cookies_ajax
views def test_user(request): print('start') if request.method=='POST': print('goon_test_user') user ...
- UICollectionView setPrefetchingEnabled
UICollectionView 开启是否开启预加载,如果开启,cell在没显示的时候就回去调用cellForIndex…方法,如果没开启,cell只有在显示的时候才会去调用cellForIndex… ...
- es6初级之解构----之二 及 键值反转实现
1.解构: 不定参数,扩展表达式 let arr = [100, 201, 303, 911]; let [one, ...others] = arr; console.log(others.leng ...
- ACM__最小生成树之prime
今天做了一道题,根本没想到最小生成树,稀里糊涂的浪费了很多时间,复习一下 转载自https://www.cnblogs.com/zhangming-blog/p/5414514.html Prim算法 ...
