AGC043E

抄一下 https://www.luogu.com.cn/article/n32presk，写的非常好。

下面是要把问题转化为一个群论问题。

定义拓扑空间：全集 \(X\) 和它的一个子集族 \(T\)，使得 \(\varnothing,X\in T\)，且任意有限个元素的交在 \(T\) 中，任意元素（不要求有限或可数）的并在 \(T\) 中。

则称 \((X,T)\) 是拓扑空间，\(T\) 内元素叫开集，不在的是闭集。

拓扑空间之间的函数 \(f:X\to Y\) 是连续的，当且仅当 \(\forall t\in T_Y\)，\(f^{-1}(t)\in T_X\)（数学分析中有形式一样的度量空间上的结论）

对于这道题，不用太在意这个定义，因为 \(\R,\R^2\) 及其子空间的开集概念是熟知的。

下记 \(S^1\) 为单位圆（就是首尾相接的 \([0,1]\)）。

对于拓扑空间 \(X\)，一条道路是 \(f:[0,1]\to X\) 的函数，一条闭曲线/回路是 \(f:S^1\to X\) 的连续函数。

下面一段直接在道路 \(C,D:X\to Y\) 的意义下说了。

闭曲线 \(C\) 到 \(D\) 存在连续变化，当且仅当存在连续函数 \(F:X\times [0,1]\to Y\)，使得 \(F(x,0)=C(x),F(x,1)=D(x)\)，此时称 \(C,D\) 同伦。若还满足 \(F(0,x)=C(0)=D(0),F(1,x)=C(1)=D(1)\)，这称为定端同伦，记为 \([C]=[D]\)。

定端同伦关系构成等价类，即 \([C]\) 代表和 \(C\) 定端同伦的等价类。

定义道路 \(C(0)=x,C(1)=D(0)=y,D(1)=z\) 的乘积 \(C*D\)：把 \(C\) 放在 \([0,0.5]\)，\(D\) 放在 \([0.5,1]\)，显然还是连续；扩展到等价类上，等价类的 \(*\) 是满足

\[[C]*[D]=[C*D]
\]

的运算。

对于定点 \(z\) 到自己的回路，这样的等价类和 \(*\) 构成群，其中单位元 \(e\mapsto e(x)=z\)，而把回路翻转构成了逆元。这称为基本群 \(\pi(X,z)\)。

一个拓扑空间 \(X\) 有强形变收缩核 \(A\subset X\)，当 \(e(x)=x\) 和一个连续函数 \(r:X\to A\) 同伦，且同伦函数 \(H\) 满足 \(\forall a\in A,t,H(a,t)=a\)（即 \(A\) 内部不变）。这个同伦把 \([f]\in \pi(X,z)\) 同到了 \([r\circ f]\in \pi(A,z)\)。

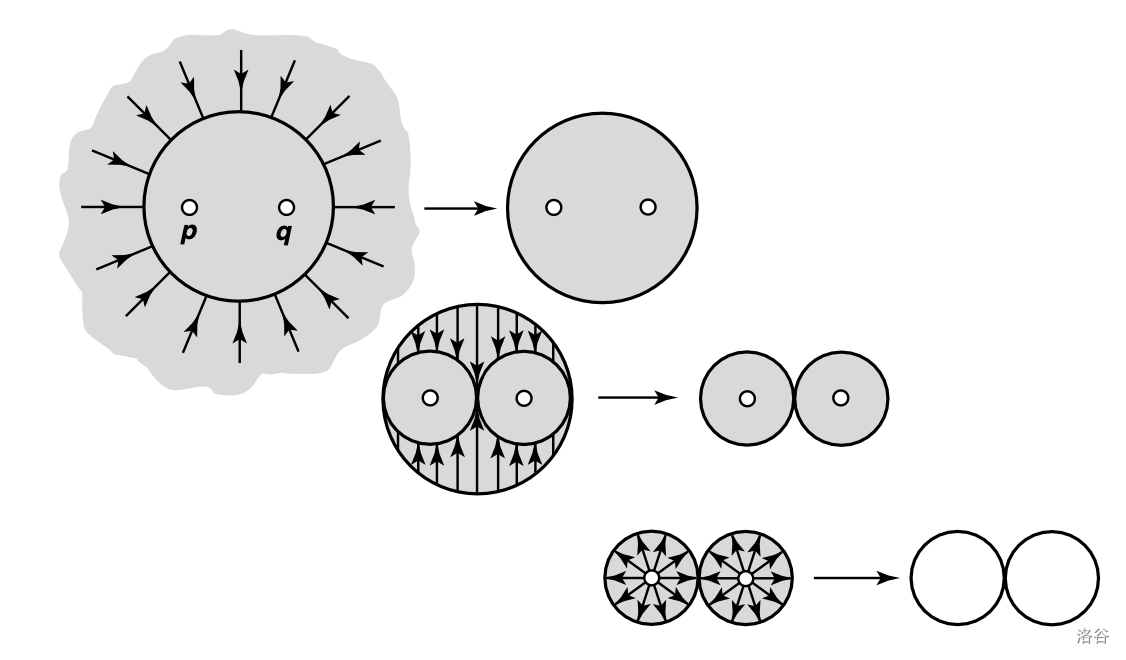
这表明 \(\R^2-\{x\}-\{y\}\) 可以收缩到两个 \(S^1\) 在一个点上拼起来，记为 \(S^1\lor S^1\)。显然，\(\R^2-\{x_1,x_2\dots x_n\}\) 可以收缩到 \(S^1\lor S^1\lor\dots \lor S^1\)，只需考虑 \(\pi(S^1\lor S^1\lor\dots \lor S^1,z)\) 的结构。

不难看出（？） \(\pi (S^1,z)=\Z\)。而有：

塞弗特-范坎彭定理：\(\pi(A\cup B,z)=\pi(A,z)*\pi(A\cap B,z)*\pi(B,z)\)，其中 \(*\) 是群自由积。

所以，\(\pi(S^1\lor S^1\lor\dots \lor S^1,z)=\Z*\Z*\dots *\Z\)。对于本题的条件，记点集为 \(S=\{x_1,x_2,\dots x_n\}\)；这可以被看作是 \(x_i\) 及 \(x_i^{-1}\) 构成的串集合。

对于 \(T\subset S\)，考虑嵌入 \(\iota :\R^2-S\to \R^2-T\) 及其给出的同态 \(\varphi_{S\to T}:\pi(\R^2-S,z)\to \pi(\R^2-T,z)\)，这个同态具体是对于 \(i\not\in T\)，\(x_i\) 成为单位元 \(e\)，否则不变，而这些 \(i\to T\) 的自由群就是 \(\R^2-T\)。

一个闭曲线是同伦于单位元 \(e\) 的。那么问题变为：

对于一个自由群 \(F(x_1,x_2\dots x_n)\)，找出 \(w\in F\)，使得 \(\forall T\subset S,[\varphi_{S\to T}(w)=e]=A_T\)。

首先必须满足 \(A_0=1\)，并且 \(\forall R\subset T,A_R\ge A_T\)。下面构造展示，这也是充要条件。

记两元素的交换子是 \([x,y]=xyx^{-1}y^{-1}\)。由于同态性，\(\varphi([x,y])=[\varphi(x),\varphi(y)]\)。这有的好性质是 \([e,x]=[x,e]=e\)。

记 \(w_x=x\)，\(w_{S}=w_{\{x_1,x_2\dots x_m\}}=[w_x,w_{S-\{x_1\}}]\)。如果限制为 \(A_T=[S\neq T]\)，则可构造 \(w_S\) 满足条件（可以归纳验证）。

进一步地，取出极小的 \(A_{R_i}=0\)。则可以验证，

\[\prod_i w_{R_i}
\]

满足条件。总路径长度是 \(O(n3^n)\) 的。

#include<bits/stdc++.h>
using namespace std;
#define pt array<int,2>
struct loop{vector<pt> a;};
loop inv(loop A){reverse(A.a.begin(),A.a.end());return A;}
loop operator *(loop A,loop B){
	loop C;
	for(auto u:A.a)C.a.push_back(u);
	for(int i=1;i<B.a.size();i++)C.a.push_back(B.a[i]);
	return C;
}
loop operator ^(loop A,loop B){
	return A*B*inv(A)*inv(B);
}
loop w(int x){
	loop A;A.a.push_back({0,0});
	for(int i=1;i<=x+1;i++)A.a.push_back({i,0});
	A.a.push_back({x+1,1});
	A.a.push_back({x,1});
	for(int i=x;i>=0;i--)A.a.push_back({i,0});
	return A;
}
loop w(vector<int> S){
	if(S.size()==1)return w(S[0]);
	int x=S.back();S.pop_back();
	return w(S)^w(x);
}
int A[(1<<6)+5],n;
string str;
vector<int> getS(int x){
	vector<int> S;
	for(int i=0;i<n;i++)if(x&(1<<i))S.push_back(i);
	return S;
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>str;
	for(int i=0;i<(1<<n);i++)A[i]=str[i]-'0';
	int flg=A[0]==1;
	for(int i=0;i<(1<<n);i++)for(int j=0;j<(1<<n);j++)if((i&j)==j)flg&=(A[j]>=A[i]);
	if(!flg)return cout<<"Impossible"<<endl,0;
	cout<<"Possible"<<endl;
	loop ans;ans.a.push_back({0,0});
	for(int i=0;i<(1<<n);i++){
		if(A[i]==1)continue;
		bool cf=1;
		for(int j=0;j<i;j++)if((i&j)==j&&A[j]==0)cf=0;
		if(cf)ans=ans*w(getS(i));
	}
	cout<<ans.a.size()-1<<endl;
	for(auto [x,y]:ans.a)cout<<x<<" "<<y<<endl;
	return 0;
}

又快又好写，不知道为什么第一篇点赞更多。