目标检测 | 基于Weiler–Atherton算法的IoU求解

IoU

交并比（Intersection over Union, IoU） 是计算机视觉领域中常用的一个评价指标，尤其在目标检测与图像分割任务中，用于衡量预测结果与真实标注之间的重合程度。

其定义如下：

如图所示给定任意两个多边形框$B_1, B_2$（预测框与真实框），其 IoU 的计算公式为：

\[\text{IoU}(B_1, B_2) = \frac{|B_1 \cap B_2|}{|B_1 \cup B_2|}
\]

其中$|B_1 \cup B_2|$为二者并集的面积，$|B_1 \cap B_2|$为二者交集的面积。

IoU的取值范围为$[0,1]$，当$IoU=1$时表示预测框与真实框完全一致；当$IoU=0$时表示预测框与真实框没有任何重叠；

通过评价$IoU$可以评估目标检测模型的性能

基于Weiler–Atherton算法的IoU求解

Bounding Box

在目标检测任务中，通常使用 包围盒（bounding box） 表示目标的矩形区域。根据任务需求的不同，包围盒可以分为以下几类：

轴对齐包围盒（Axis-Aligned Bounding Box，AABB）

轴对齐包围盒一般应用于2D的目标检测任务，四条边分别与x轴和y轴对齐，可以表达为：

\[B_\text{AABB} = (x_c, y_c, w, h),
\quad w > 0, \, h > 0
\]
- 其中$(x_c,y_c)$为中心坐标，$w,h$分别为包围盒的宽和高，也被称为外延（extent）
BEV包围盒（Bird’s Eye View Bounding Box，BEV Boudning Box）

BEV包围盒一般用于自动驾驶任务，在俯视图（BEV）中，每个物体除了位置和尺寸外，还包含一个航向角（yaw）表示方向，可以表达为：

\[B_\text{BEV} = (x_c, y_c, l, w, \theta),
\quad l > 0, \, w > 0, \, \theta \in [-\pi, \pi)
\]
- 其中$(x_c,y_c)$为中心坐标，$l,w$分别为包围盒的长和宽，$\theta$为全局坐标系的旋转角度
3D包围盒（3D Boudning Box）

3D包围盒在BEV包围盒的基础上增加了高度，也是自动驾驶任务中常用的表示格式

\[B_\text{3D} = (x_c, y_c, z_c, l,w,h, \theta),
\quad w, l, h > 0, \, \theta \in [-\pi, \pi)
\]
- 其中$(x_c,y_c,z_c)$为中心坐标，$l,w,h$分别为包围盒的长，宽和高，$\theta$为全局坐标系的旋转角度

在本文中，我们以 BEV 包围盒 为例，使用 Weiler–Atherton 算法求解 IoU。对于3D包围盒的 IoU 计算，可通过将 BEV 包围盒在俯视平面上的结果拓展到高度方向来实现。

Corner坐标转换

在计算之前，我们首先需要将多边形从包围盒表示转换为Corner坐标表示（四个顶点的坐标），这个过程可以分为三步，首先给定一个包围盒：

\[B_\text{BEV} = (x_c, y_c, l, w, \theta),
\quad l > 0, \, w > 0, \, \theta \in [-\pi, \pi)
\]

计算局部坐标系下的四个角点

\[P^\text{local} =
\begin{bmatrix}
+\frac{l}{2} & +\frac{w}{2} \\
+\frac{l}{2} & -\frac{w}{2} \\
-\frac{l}{2} & -\frac{w}{2} \\
-\frac{l}{2} & +\frac{w}{2}
\end{bmatrix} \in \mathbb{R}^{4\times 2}
\]

绕中心旋转矩阵

\[P^\text{rotated} = P^\text{local} \cdot R(\theta)^\top
\]

其中：

\[R(\theta) =
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}
\]

平移到全局坐标系

\[P^\text{global}=P^\text{rotated}+
\begin{bmatrix} x_c & y_c \\ x_c & y_c \\ x_c & y_c \\ x_c & y_c \end{bmatrix}
\]

将上述的三个过程合并为齐次坐标系矩阵：

\[\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1 \\
x_4 & y_4 & 1
\end{bmatrix} =
\begin{bmatrix}
+ \frac{l}{2} & + \frac{w}{2} & 1 \\
+ \frac{l}{2} & - \frac{w}{2} & 1 \\
- \frac{l}{2} & - \frac{w}{2} & 1 \\
- \frac{l}{2} & + \frac{w}{2} & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
\cos\theta & \sin\theta & x_c \\
-\sin\theta & \cos\theta & y_c \\
0 & 0 & 1
\end{bmatrix}
\]

Weiler–Atherton算法

Weiler–Atherton算法是一种计算任意两个非凹图形交集的算法，可以被分为四个步骤：

求解所有相交点
求解所有被包围的顶点
将相交点和被包围的顶点放入一个数组中，按照逆时针进行排序
按照顺序连接为新的多边形求解其面积

给定任意两个包围盒的Cornor坐标表示$B_1,B_2\in\mathbb{R}^{4 \times 2}$

计算所有相交点

给定任意两条线段$L_1=(x_1,y_1),L_2=(x_2,y_2)$与$M_1=(x_3,y_3),M_2=(x_4,y_4)$，我们可以如下求出其交点：

定义$r=L_2-L_1,s=M_2-M_1$，有：

\[t=\frac{(M_1-L_1)\times s}{r\times s},u=\frac{(M_1-L_1)\times r}{r\times s}
\]

其中$\times$为二维向量叉乘，定义如下：

\[(x_1,y_1)\times(x_2,y_2)=x_1y_2 - y_1x_2
\]

那么线段$P,Q$的交点为：

\[P_{insect}=
\begin{cases}
L_1 + t r, &
\text{if } r\times s \neq 0 \text{ and } t \in [0,1], u \in [0,1] \\[1ex]
\text{无交点}, & \text{otherwise}
\end{cases}
\]

通过线段相交算法我们可以求出任意两个线段之间的交点（如图所示的紫色点）

计算所有被对方包围起来的顶点

给定任意一个包围盒$B\in\mathbb{R}^{4 \times 2}$与点$P$，我们可以通过如下过程求解点$P$是否在包围盒$B$中：

定义$P_a=B[0, :],P_b=B[1, :],P_d=B[3, :]$

求得：

\[t=\frac{AP\cdot AB}{||AB||^2},u=\frac{AP\cdot AD}{||AD||^2}
\]

其中$AB=P_b-P_a,\ AD=P_d-P_a,\ AP = P-P_a$

如图所示，当$t\in[0,1]\and u\in[0,1]$时，点$P$位于包围盒中$B$

通过上述流程我们可以求解所有在对方包围盒的顶点（如图所示的绿色点）

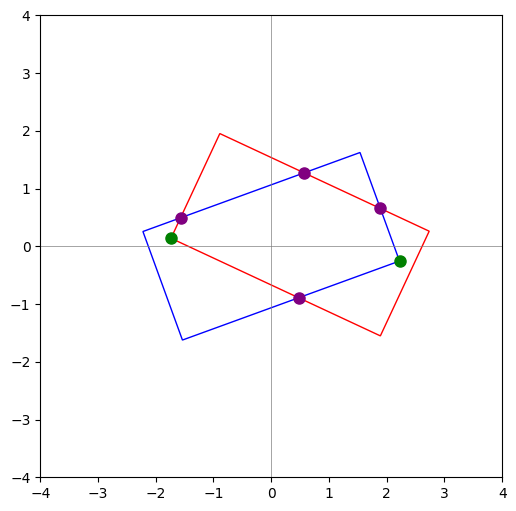
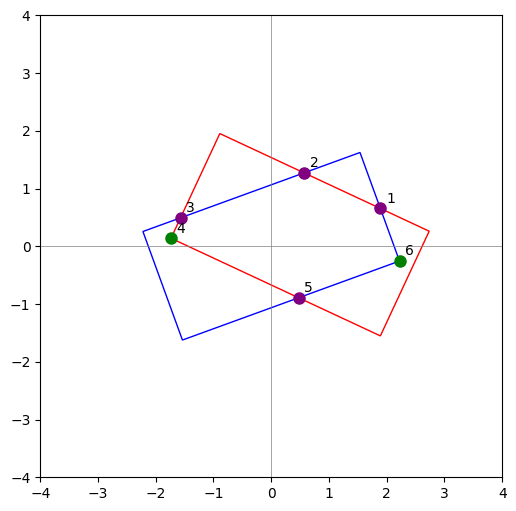
顶点极角排序

为了方便连接每个顶点，接下来我们将所有顶点按照极坐标系下的角度进行排序，给定任意两点$P_1(x_1,y_1)$与$P_2(x_2,y_2)$，有比较函数如下：

\[\text{cmp}(P_1,P_2) =
\begin{cases}
\text{true}, & \Theta_{P_1} < \Theta_{P_2} \\[0.5em]
\text{false}, & \Theta_{P_1} \geq \Theta_{P_2} \\[0.5em]
\end{cases}
\]

其中

\[\Theta_P =
\begin{cases}
\arctan2(y, x), & \arctan2(y, x) \ge 0 \\
\arctan2(y, x) + 2\pi, & \arctan2(y, x) < 0
\end{cases}
\]

但是$\arctan2$这个操作非常消耗资源，所以我们不会直接计算极角$\theta $，我们会进行如下优化：

给定极坐标系的坐标$(r,\theta) $，我们可以构建一个关于$\theta$的函数$g(\theta)=|\cos\theta|\cos\theta$，这个函数会在第一，二象限递减，第三，四象限递增，接下来有：

\[\begin{align}
g(\theta) & = \frac{r^2}{r^2} \, g(\theta) \\
& =\frac{r^2 \, |\cos\theta| \cos\theta}{r^2}\\
& =\frac{|r \cos\theta| \cdot (r \cos\theta)}{r^2} \\
\end{align}
\]

其中我们将极坐标系公式代入原式：

\[x = r \cos\theta, \quad y = r \sin\theta, \quad r = \sqrt{x^2 + y^2}
\]

得到：

\[\begin{align}
g(\theta) &=\frac{|r \cos\theta| \cdot (r \cos\theta)}{r^2} \\
&=\frac{|x|\cdot x}{x^2+y^2}
\end{align}
\]

在实际计算中为了防止除0我们会在分母加上一个非常小的数$\varepsilon$：

\[g(\theta) =\frac{|x|\cdot x}{x^2+y^2+\varepsilon}
\]

我们可以给出优化版本的比较函数$\text{cmp}(\cdot,\cdot)$：

\[\text{cmp}(P_1,P_2) =
\begin{cases}
\text{false}, & (x_1,y_1) = (x_2,y_2) \\[0.5em]
\text{true}, & y_1 > 0,\, y_2 < 0 \\[0.5em]
\text{false}, & y_1 < 0,\, y_2 > 0 \\[0.5em]
\text{true}, & y_1 > 0,\, y_2 > 0,\, g(\theta_1) > g(\theta_2) \\[0.5em]
\text{true}, & y_1 < 0,\, y_2 < 0,\, g(\theta_1) < g(\theta_2) \\[0.5em]
\end{cases}

\text{其中 }
g(\theta) = \frac{|x|\cdot x}{x^2+y^2+\varepsilon}
\]

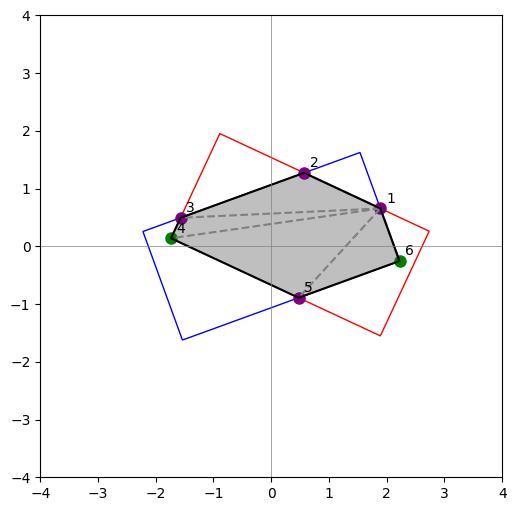
形成新的多边形并计算面积

给定任意二维向量$L=(x_1,y_1),M=(x_2,y_2)$，我们可以求解二者共同起点所构成的三角形面积$S_{LM}$：

\[S_{LM}=\frac{1}{2}|L\times M|=\frac{1}{2}|x_1y_2-y_1x_2|
\]

给定已经按照极角进行排序的点集$\{P_1,\dots,P_n|n\leq8\}$，我们可以将这些点按照顺序连接为一个闭合的多边形$I$，这个多边形由$n-2$个三角形所组成，每个三角形$S_n$的面积为$S_n=\frac{1}{2}|(P_{n+1}-P_1)\times (P_{n+2}-P_1)|$，那么我们可以算出这个多边形的面积：

\[S_{I}=\sum^{n-2}_{i=1}\frac{1}{2}|(P_{i+1}-P_1)\times (P_{i+2}-P_1)|
\]

计算IoU

上文我们已经得到BEV包围盒$B_1$与$B_2$的交集面积为$S_I$，那么我们可以如下算得$IoU$：

\[IoU =\frac{Intersection}{Union}= \frac{S_I}{S_{B_1}+S_{B_2}-S_I}
\]

如果$B_1,B_2$为3D包围盒，可以如下增加一个高度项：

\[IoU =\frac{Intersection}{Union}= \frac{H_I}{H_U}\frac{S_I}{S_{B_1}+S_{B_2}-S_I}
\]

其中

\[\begin{align}
H_I=&\max(0,\min(z_{B_1}+\frac{h_{B_1}}{2}, z_{B_1}+\frac{h_{B_2}}{2})-\max(z_{B_1}-\frac{h_{B_1}}{2},z_{B_2}-\frac{h_{B_2}}{2}))\\H_U=&h_{B_1}+h_{B_2}-H_I
\end{align}
\]

参考文献

https://en.wikipedia.org/wiki/Weiler–Atherton_clipping_algorithm

https://github.com/lilanxiao/Rotated_IoU