vue源码分析之new Vue过程

实例化构造函数

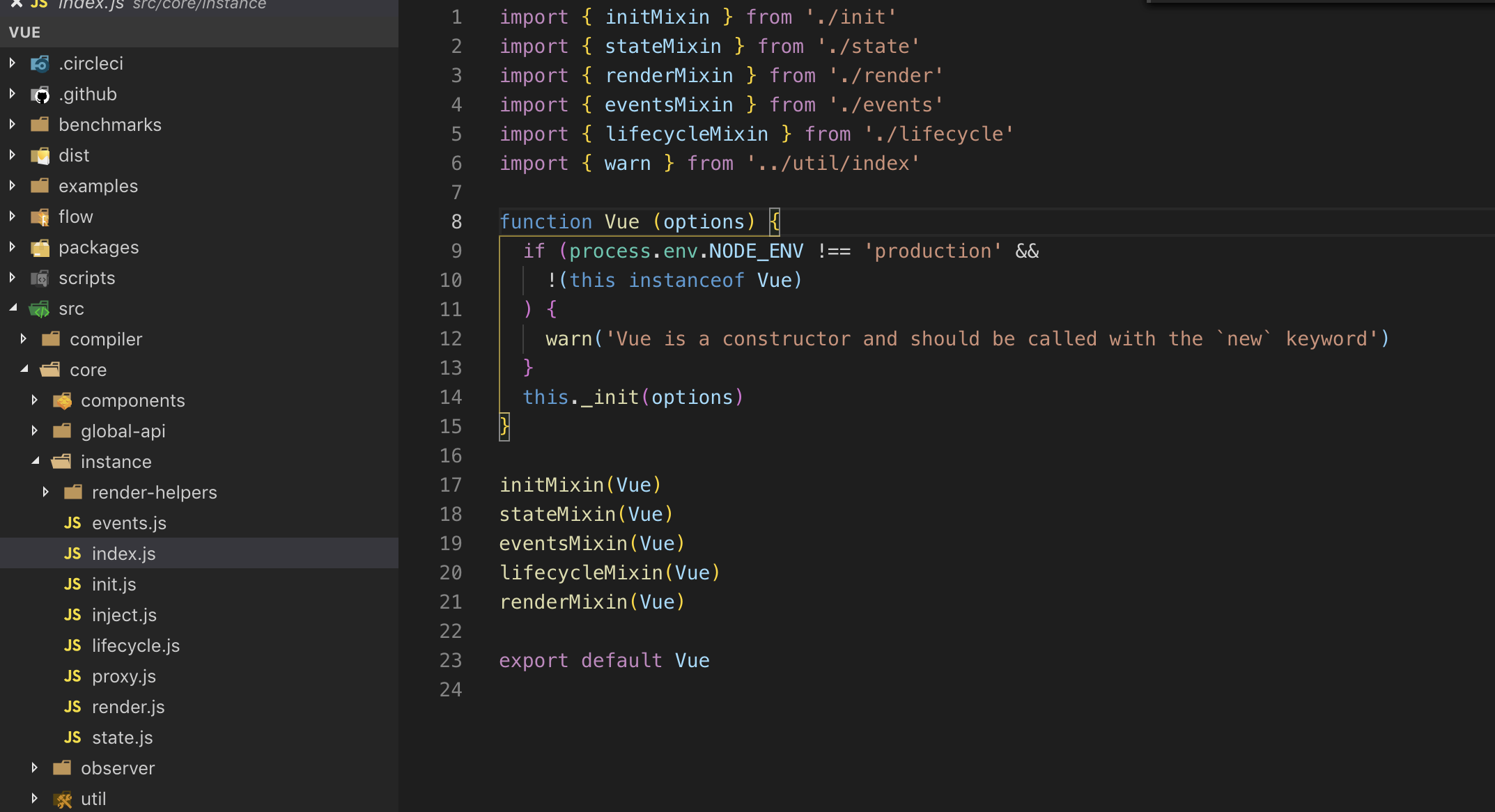
从这里可以看出new Vue实际上是使vue构造函数实例化，然后调用_init方法

_init方法,该方法在 src/core/instance/init.js 中定义

Vue.prototype._init = function (options?: Object) {
    const vm: Component = this
    // a uid
    vm._uid = uid++

    let startTag, endTag
    /* istanbul ignore if */
    if (process.env.NODE_ENV !== 'production' && config.performance && mark) {
      startTag = `vue-perf-start:${vm._uid}`
      endTag = `vue-perf-end:${vm._uid}`
      mark(startTag)
    }

    // a flag to avoid this being observed
    vm._isVue = true
    // merge options
    if (options && options._isComponent) {
      // optimize internal component instantiation
      // since dynamic options merging is pretty slow, and none of the
      // internal component options needs special treatment.
      initInternalComponent(vm, options)
    } else {
      vm.$options = mergeOptions(
        resolveConstructorOptions(vm.constructor),
        options || {},
        vm
      )
    }
    /* istanbul ignore else */
    if (process.env.NODE_ENV !== 'production') {
      initProxy(vm)
    } else {
      vm._renderProxy = vm
    }
    // expose real self
    vm._self = vm
    initLifecycle(vm)
    initEvents(vm)
    initRender(vm)
    callHook(vm, 'beforeCreate')
    initInjections(vm) // resolve injections before data/props
    initState(vm)
    initProvide(vm) // resolve provide after data/props
    callHook(vm, 'created')

    /* istanbul ignore if */
    if (process.env.NODE_ENV !== 'production' && config.performance && mark) {
      vm._name = formatComponentName(vm, false)
      mark(endTag)
      measure(`vue ${vm._name} init`, startTag, endTag)
    }

    if (vm.$options.el) {
      vm.$mount(vm.$options.el)
    }
  }

Vue 初始化主要就干了几件事情，传入option，合并option配置，初始化生命周期，初始化事件中心，初始化渲染，初始化 data、props、computed、watcher 等等