P5239 回忆京都（洛谷3月月赛T2）

题目描述

射命丸文在取材中发现了一个好玩的东西，叫做组合数。

组合数的定义如下：从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。所有组合的数量，就是组合数。

$\sum_{i=1}^n \sum_{j=1}^m C^i_j$，其中当i>j的时候，钦定$C^i_j$​为0

她也很快就算出来了，不过对自己的答案不是很充满信心，因此你决定帮助她。然而没事找事的她一下子算了q次对于不同的n,m的结果，因此这只能劳烦你了。由于你不打算真正地帮助她，你无需把答案对998244353取模，也无需对64123取模，只要告诉她对取模之后的答案即可。

输入输出格式

输入格式：

第一行输入一个q，表示有q次询问。

第二行开始，一共q行，每行两个数字n,m，意思如题所示。

输出格式：

一共q行，对于每一个询问，都输出一个答案。

数据范围：n,m<=1000

solution

容易想到预处理出杨辉三角, c[i][j]表示$c^j_i$ %mod，递推公式是c[i][j]=c[i-1][j]+c[i-1][j-1]，注意处理c[i][0]=1;

这样每次询问是O(nm)，总的时间复杂度是O(qnm)，TLE3个点，需要优化

通过模拟发现，题目中要求的数的和实际上在杨辉三角中是一个矩形的区域，也就是右下角下标为c[m][n]

例如，当m=4,n=3时，就是矩形区域的和，所以只需要维护一个二维前缀和就行了

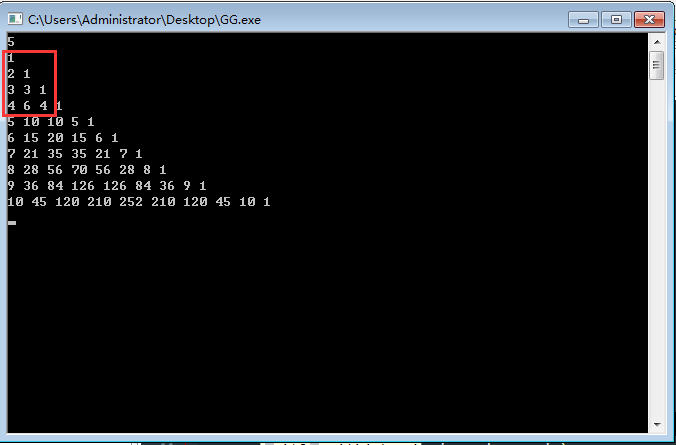
一个大坑：当预处理二维前缀和时因为经过了取模，所以容易出现新的前缀和为负数的情况，而我们希望得到的一定是个正数，所以每一项s[i][j]=(s[i][j]+mod)%mod;

因为这个坑WA了三个

code

#include<cstdio>
#include<iostream>
#include<cstring>
#define mod 19260817//咳咳
#define maxn 1020
using namespace std;
long long s[maxn][maxn],ts[maxn][maxn];
int n,m,t,x,ans,tmp;
void init(int n)
{
    for(int i=;i<=n;++i)
    {
        s[i][]=;
    }
    for(int i=;i<=n;++i)
    {
        for(int j=;j<=n;++j)
        {
            if(j<=i) s[i][j]=(s[i-][j]+s[i-][j-])%mod;//杨辉三角 

            ts[i][j]=(ts[i-][j]+ts[i][j-]-ts[i-][j-]+s[i][j]+mod/*关键*/)%mod;//二维前缀和
        }

    }

}
int main()
{
    scanf("%d",&t);
    init();//预处理杨辉三角与前缀和
    for(int k=;k<=t;++k)
    {
        scanf("%d%d",&n,&m);
        printf("%lld\n",ts[m][n]);
    }
    return ;
}