PCA算法和python实现

第十三章 利用PCA来简化数据

一．降维技术

当数据的特征很多的时候，我们把一个特征看做是一维的话，我们数据就有很高的维度。高维数据会带来计算困难等一系列的问题，因此我们需要进行降维。降维的好处有很多，比如：降低算法开销，让数据更加便于使用，去燥，数据更易于显示等等。

目前的降维技术主要有三种：第一种主成分分析（PCA），也就是本章介绍的内容，它只保留方差方向最大的若干个特征；第二种是因子分析，这种方法它的思想就是认为数据是由隐参数和噪声混合而成，如果我们能够找到隐参数和噪声就能够实现降维；第三种是独立成分分析（ICA），这种方法的思想是它认为数据是由若干个独立的数据源混合而成，如果我们能够找到这些数据源，就能够实现降维。

二．PCA的基本思想

PCA就是把一个高维的空间映射到一个低维的空间，这个低维的空间，让样本点的投影尽可能的分开，距离尽可能的大。要找到这样的一个低维空间，我们是通过不断的选择方差最大的方向来作为新特征维度实现的，当选择的方向的数目少于初始的特征维度，就实现了降维。

PCA算法的一般特性：

1.它的优点：降低数据的复杂度

2.它的缺点：可能用不到，会丧失一些有用的信息

3.它的使用类型：数值型数据

PCA算法实现的一般过程：

1.进行去中心化（也就是将每个数据减掉它的平均值）

2.计算X^TX，也就是计算出协方差矩阵

3.计算协方差矩阵的特征向量和特征值

4.将得到的特征值进行从小到大的排列，然后选择值最大的d个特征值对应的特征向量作为新空间的方向向量

5.将数据映射到新的空间

三．PCA算法的实现

根据PC A算法的一般过程我们可以得到以下的实现方式：

首先我们需要获得数据

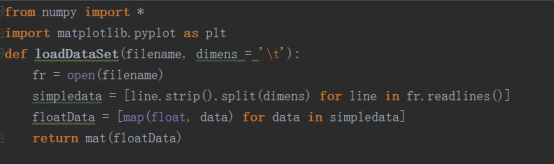
其次我们就能够定义PC A算法了

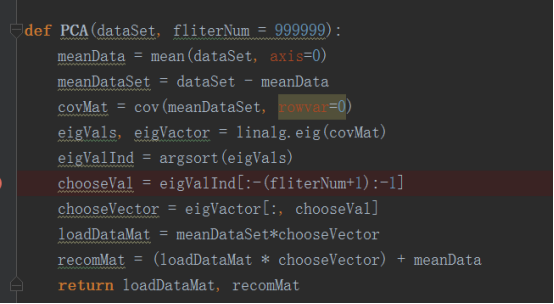
四．总结

PC A算法是一种进行降维的重要方法。我们在选择保留的特征的数目时，我们既可以实现设定，也可以根据得到特征值来进行选择。保留合适的特征数目对于数据非常的重要。

当前的降维方法主要有三种，一种是独立成分分析，一种是主成分分析，还有一种就是因子分析。主成分分析是一种应用比较广泛的方法。主成分分析他通过不断选择数据方差最大的方向来实现降维。