漫谈“采样”（sampling）

越学越懵了，计算机中是怎么进行采样的，用了这么久的 rand() 函数，到现在才知道是怎么做的。

从均匀分布中采样

计算机中通过线性同余发生器（linear congruential generator，LCG）很容易从一个 $ x \sim Uniform[0, 1)$ 的均匀分布中进行采样。如果要从 $y \sim Uniform[a, b)$ 的均匀分布中采样，只需要 $x$ 的基础上做个变换 $y = (b-a)x + a$ 即可。

当然除了 LCG 外，还有其它均匀分布随机数生成方法，这里不一一列举，可以参考博客随机数生成（一）：均匀分布。

单独把均匀分布采样摘出来是因为它很基础，很多其它采样方法都是在该基础上进行操作。

对离散型变量采样

我们现在通过某种方法（比如 LCG）可以生成均匀分布的随机数，这个时候我们就完全可以对某个含有有限个离散取值的变量 $r$ 进行采样，方法就是采用轮盘赌选择法。

假设离散型变量 $r$ 有 3 个取值，$a_1, a_2, a_3$，概率分布如下图所示：

图 1 离散型变量 $r$ 概率分布

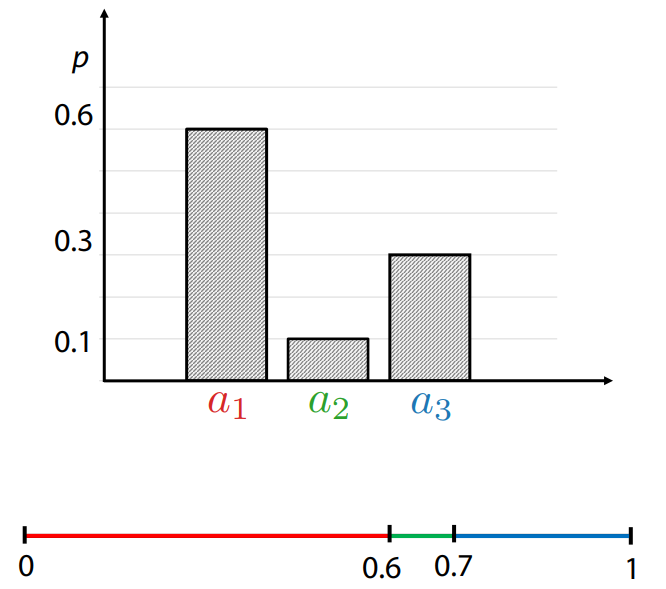
所有取值概率之和为 1。此时我们可以从 $Uniform[0, 1)$ 生成一个随机数 $b$，若 $0 \le b < 0.6$，则选择出 $a_1$；若 $0.6 \le b < 0.7$，则选择出 $a_2$；若 $0.7 \le b < 1$，则选择出 $a_3$。

对连续型变量采样

上面我们已经讨论了从均匀分布 $U[a,b)$ 中采样，对于其余分布，如高斯分布、gamma 分布、指数分布、t 分布、F 分布、Beta 分布、Dirichlet 分布等等，都可以基于 $U[0,1)$ 的样本生成。例如高斯分布可以通过 Box-Muller 变换得到：

【Box-Muller 变换】如果随机变量 $U_1,U_2$ 独立且 $U_1,U_2 \sim Uniform[0, 1]$，
\[
\begin{aligned}
Z_0 = \sqrt{-2\ln U_1} \cos (2 \pi U_2) \\
Z_1 = \sqrt{-2\ln U_1} \sin (2 \pi U_2)
\end{aligned}
\]

则 $Z_0, Z_1$ 独立且服从标准正态分布。

想要得到服从 $Z_2 \sim N(\mu, \sigma^2)$ 的高斯分布，则只需对 $Z_0 \sim N(0, 1)$ 做如下变换：
\[
Z_2 = \sigma Z_0 + \mu
\]

对于更加一般分布 $p(x)$，如下图所示，我们该如何对其进行采样呢？

图 2 分布 $p(x)$

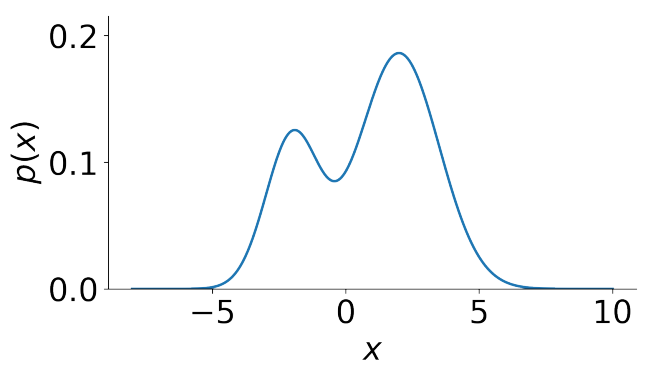
这个时候我们可以使用 rejection sampling。

Rejection sampling 首先寻找一个简单的分布 $q(x)$，然后乘以一个常数 $M$，使其满足 $p(x) \le M \cdot q(x)$，如下图所示，$q(x)$ 是一个高斯分布，$M = 2$。

图 2 分布 $p(x)$ 和分布 2q(x)

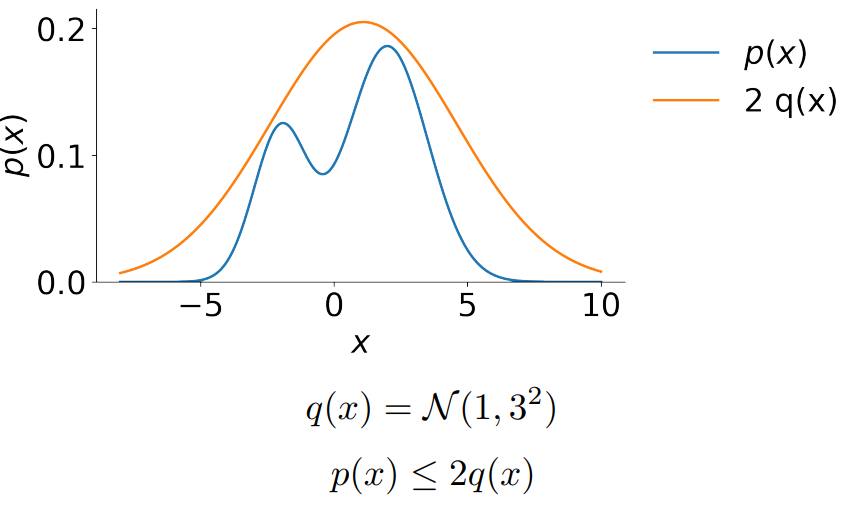
在找到一个分布 $2q(x)$ 能完全“覆盖”分布 $p(x)$ 后，我们任意 sample 一个样本点 $x_i$，但此时，我们将以 $\frac{p(x_i)}{2q(x_i)}$ 的概率选择去接收这个样本，以 $(1 - \frac{p(x_i)}{2q(x_i)})$ 的概率选择去拒绝该样本。rejection sampling 平均会接收 $\frac{1}{M}$ 个样本点。

rejection sampling 优点：使用 rejection sampling 可以对大多数分布进行采样，即使这些“分布”没有进行归一化。

rejection sampling 缺点：当 $p(x)$ 和 $2q(x)$ 相差太多时，rejection sampling 将拒绝大多数样本点；其次，对于高维数据，常数 $M$ 会很大，简单使用 rejection sampling 所需要的样本量随空间维数增加而指数增长，即高维情况下不适合用 rejection sampling，此时 MCMC（Markov Chains Monte Carlo）和 Gibbs sampling 才是主流。（当然 MCMC 等既能处理离散情况也能处理连续情况。）

References

线性同余发生器 -- 百度百科
 随机数生成（一）：均匀分布 -- MoussaTintin
LDA-math-MCMC 和 Gibbs Sampling -- 靳志辉
 MCMC(一)蒙特卡罗方法 -- 刘建平Pinard
Bayesian Methods for Machine Learning: Sampling from 1-d distributions