常用七大经典排序算法总结(C语言描述)

简介

　　其中排序算法总结如下：

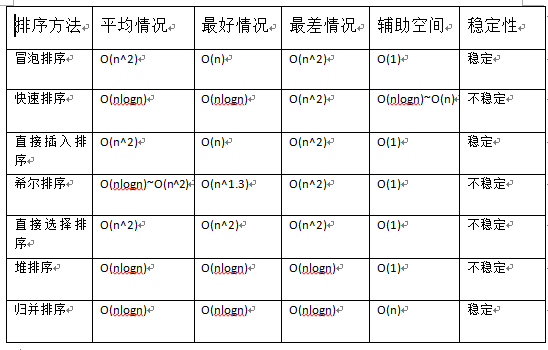
一.交换排序

　　交换排序的基本思想都为通过比较两个数的大小，当满足某些条件时对它进行交换从而达到排序的目的。

1.冒泡排序

　　基本思想：比较相邻的两个数，如果前者比后者大，则进行交换。每一轮排序结束，选出一个未排序中最大的数放到数组后面。

#include<stdio.h>
//冒泡排序算法
void bubbleSort(int *arr, int n) {
    for (int i = ; i<n - ; i++)
        for (int j = ; j < n - i - ; j++)
        {
            //如果前面的数比后面大，进行交换
            if (arr[j] > arr[j + ]) {
                int temp = arr[j]; arr[j] = arr[j + ]; arr[j + ] = temp;
            }
        }
}
int main() {
    int arr[] = { ,,,,,,,,, };
    int n = sizeof(arr) / sizeof(int);
    bubbleSort(arr, n);
    printf("排序后的数组为：\n");
    for (int j = ; j<n; j++)
        printf("%d ", arr[j]);
    printf("\n");
    return ;

分析：

　　最差时间复杂度为O(n^2),平均时间复杂度为O(n^2)。稳定性：稳定。辅助空间O(1)。

　　升级版冒泡排序法：通过从低到高选出最大的数放到后面，再从高到低选出最小的数放到前面，如此反复，直到左边界和右边界重合。当数组中有已排序好的数时，这种排序比传统冒泡排序性能稍好。

#include<stdio.h>
//升级版冒泡排序算法
void bubbleSort_1(int *arr, int n) {
    //设置数组左右边界
    int left = , right = n - ;
    //当左右边界未重合时，进行排序
    while (left<right) {
        //从左到右遍历选出最大的数放到数组右边
        for (int i =left; i < right; i++)
        {
            if (arr[i] > arr[i + ])
            {
                int temp = arr[i]; arr[i] = arr[i + ]; arr[i + ] = temp;
            }
        }
        right--;
        //从右到左遍历选出最小的数放到数组左边
        for (int j = right;j> left; j--)
        {
            if (arr[j + ] < arr[j])
            {
                int temp = arr[j]; arr[j] = arr[j + ]; arr[j + ] = temp;
            }
        }
        left++;
    }

}
int main() {
    int arr[] = { ,,,,,,,,, };
    int n = sizeof(arr) / sizeof(int);
    bubbleSort_1(arr, n);
    printf("排序后的数组为：\n");
    for (int j = ; j<n; j++)
        printf("%d ", arr[j]);
    printf("\n");
    return ;
}

　　

2.快速排序

　　基本思想:选取一个基准元素，通常为数组最后一个元素（或者第一个元素）。从前向后遍历数组，当遇到小于基准元素的元素时，把它和左边第一个大于基准元素的元素进行交换。在利用分治策略从已经分好的两组中分别进行以上步骤，直到排序完成。下图表示了这个过程。

　　

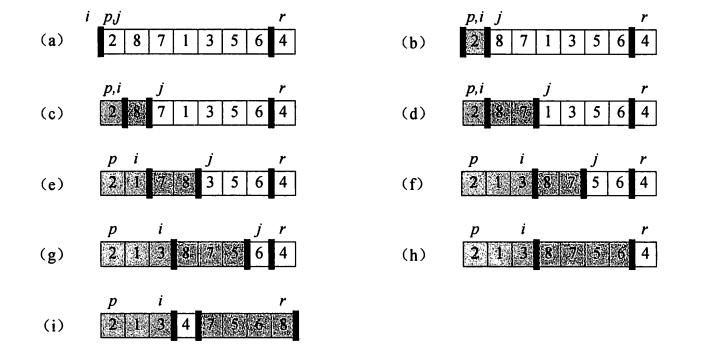
#include<stdio.h>

void swap(int *x, int *y) {
    int tmp = *x;
    *x = *y;
    *y = tmp;
}

//分治法把数组分成两份
int patition(int *a, int left,int right) {
    int j = left;    //用来遍历数组
    int i = j - ;    //用来指向小于基准元素的位置
    int key = a[right];    //基准元素
    //从左到右遍历数组，把小于等于基准元素的放到左边，大于基准元素的放到右边
    for (; j < right; ++j) {
        if (a[j] <= key)
            swap(&a[j], &a[++i]);
    }
    //把基准元素放到中间
    swap(&a[right], &a[++i]);
    //返回数组中间位置
    return i;
}
//快速排序
void quickSort(int *a,int left,int right) {
    if (left>=right)
        return;
    int mid = patition(a,left,right);
    quickSort(a, left, mid - );
    quickSort(a, mid + , right);
}
int main() {
    int a[] = { ,,,,,,,,,,,,,,, };
    int n = sizeof(a) / sizeof(int);
    quickSort(a, ,n-);
    printf("排序好的数组为：");
    for (int l = ; l < n; l++) {
        printf("%d ", a[l]);
    }
    printf("\n");
    return ;
}

分析：　　

　　最差时间复杂度：每次选取的基准元素都为最大（或最小元素）导致每次只划分了一个分区，需要进行n-1次划分才能结束递归，故复杂度为O(n^2)；最优时间复杂度：每次选取的基准元素都是中位数，每次都划分出两个分区，需要进行logn次递归，故时间复杂度为O(nlogn)；平均时间复杂度：O(nlogn)。稳定性：不稳定的。辅助空间：O(nlogn)。

　　当数组元素基本有序时，快速排序将没有任何优势，基本退化为冒泡排序，可在选取基准元素时选取中间值进行优化。

二.插入排序

　　

1.直接插入排序

　　基本思想：和交换排序不同的是它不用进行交换操作，而是用一个临时变量存储当前值。当前面的元素比后面大时，先把后面的元素存入临时变量，前面元素的值放到后面元素位置，再到最后把其值插入到合适的数组位置。　　　　　　

#include<stdio.h>
void InsertSort(int  *a, int n) {
    int tmp = ;
    for (int i = ; i < n; i++) {
        int j = i - ;
        if (a[i] < a[j]) {
            tmp = a[i];
            a[i] = a[j];
            while (tmp < a[j-]) {
                a[j] = a[j-];
                j--;
            }
            a[j] = tmp;
        }
    }
}
int main() {
    int a[] = { ,,,,,,,,,,};
    int n = sizeof(a)/sizeof(int);
    InsertSort(a, n);
    printf("排序好的数组为：");
    for (int i = ; i < n; i++) {
        printf(" %d", a[i]);
    }
    printf("\n");
    return ;
}

 分析：

　　最坏时间复杂度为数组为逆序时，为O(n^2)。最优时间复杂度为数组正序时，为O(n)。平均时间复杂度为O(n^2)。辅助空间O(1)。稳定性：稳定。

2.希尔(shell)排序

　　基本思想为在直接插入排序的思想下设置一个最小增量dk,刚开始dk设置为n/2。进行插入排序，随后再让dk=dk/2,再进行插入排序，直到dk为1时完成最后一次插入排序，此时数组完成排序。

#include<stdio.h>
//    进行插入排序
//    初始时从dk开始增长，每次比较步长为dk
void Insrtsort(int *a, int n,int dk) {
    for (int i = dk; i < n; ++i) {
        int j = i - dk;
        if (a[i] < a[j]) {    //    比较前后数字大小
            int tmp = a[i];        //    作为临时存储
            a[i] = a[j];
            while (a[j] > tmp) {    //    寻找tmp的插入位置
                a[j+dk] = a[j];
                j -= dk;
            }
            a[j+dk] = tmp;        //    插入tmp
        }
    }
}

void ShellSort(int *a, int n) {
    int dk = n / ;        //    设置初始dk
    while (dk >= ) {
        Insrtsort(a, n, dk);
        dk /= ;
    }
}

int main() {
    int a[] = { ,,,,,,,,,, };
    int n = sizeof(a) / sizeof(int);
    ShellSort(a, n);
    printf("排序好的数组为：");
    for (int j = ; j < n; j++) {
        printf("%d ", a [j]);
    }
    return ;
}

分析：

　　最坏时间复杂度为O(n^2)；最优时间复杂度为O(n)；平均时间复杂度为O(n^1.3)。辅助空间O(1)。稳定性：不稳定。希尔排序的时间复杂度与选取的增量有关，选取合适的增量可减少时间复杂度。

三.选择排序

1.直接选择排序

基本思想：依次选出数组最小的数放到数组的前面。首先从数组的第二个元素开始往后遍历，找出最小的数放到第一个位置。再从剩下数组中找出最小的数放到第二个位置。以此类推，直到数组有序。

#include<stdio.h>
void SelectSort(int *a, int n) {
    for (int i = ; i < n; i++)
    {
        int key = i;    //    临时变量用于存放数组最小值的位置
        for (int j = i + ; j < n; j++) {
            if (a[j] < a[key]) {
                key = j;    //    记录数组最小值位置
            }
        }
            if (key != i)
            {
                int tmp = a[key]; a[key] = a[i]; a[i] = tmp;    //    交换最小值
            }

    }
}
int main() {
    int a[] = { ,,,,,,,,,,,, };
    int n = sizeof(a) / sizeof(int);
    SelectSort(a, n);
    printf("排序好的数组为： ");
    for (int k = ; k < n; k++)
        printf("%d ", a[k]);
    printf("\n");
    return ;
}

分析：

　　最差、最优、平均时间复杂度都为O(n^2)。辅助空间为O(1)。稳定性：不稳定。

2.堆(Heap)排序

　　基本思想：先把数组构造成一个大顶堆（父亲节点大于其子节点），然后把堆顶（数组最大值，数组第一个元素）和数组最后一个元素交换，这样就把最大值放到了数组最后边。把数组长度n-1,再进行构造堆，把剩余的第二大值放到堆顶，输出堆顶(放到剩余未排序数组最后面)。依次类推，直至数组排序完成。

　　下图为堆结构及其在数组中的表示。可以知道堆顶的元素为数组的首元素，某一个节点的左孩子节点为其在数组中的位置*2，其右孩子节点为其在数组中的位置*2+1，其父节点为其在数组中的位置/2（假设数组从1开始计数）。

　　

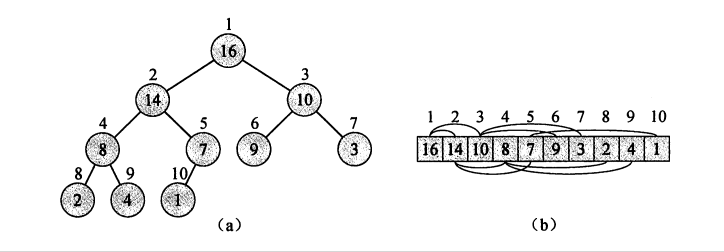
　　下图为怎么把一个无序的数组构造成一个大堆顶结构的数组的过程，注意其是从下到上，从右到左，从右边第一个非叶子节点开始构建的。

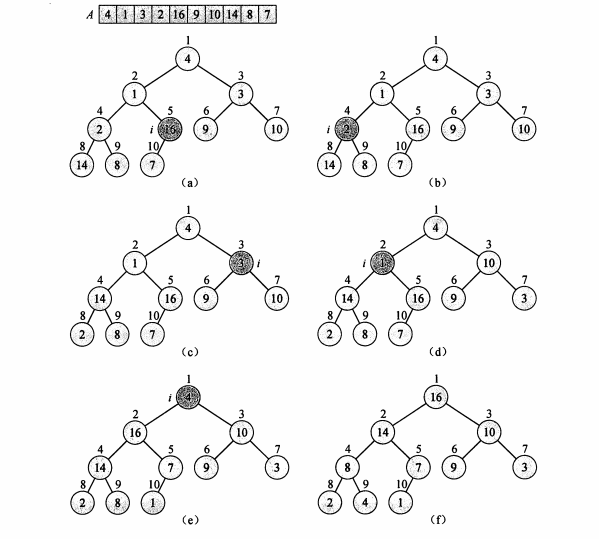
#include<stdio.h>

//　　创建大堆顶，i为当节点，n为堆的大小
//    从第一个非叶子结点i从下至上，从右至左调整结构
//    从两个儿子节点中选出较大的来与父亲节点进行比较
//    如果儿子节点比父亲节点大，则进行交换
void CreatHeap(int a[], int i, int  n) {

    //    注意数组是从0开始计数，所以左节点为2*i+1，右节点为2*i+2
    for (; i >= ; --i)
    {
        int left = i *  + ;    //左子树节点
        int right = i *  + ;    //右子树节点
        int j = ;
        //选出左右子节点中最大的
        if (right < n) {
            a[left] > a[right] ? j= left : j = right;
        }
        else
            j = left;
        //交换子节点与父节点
        if (a[j] > a[i]) {
            int tmp = a[i];
            a[i] = a[j];
            a[j] = tmp;
        }
    }
}

//    进行堆排序，依次选出最大值放到最后面
void HeapSort(int a[], int n) {
    //初始化构造堆
    CreatHeap(a, n/-, n);
　　//交换第一个元素和最后一个元素后，堆的大小减1
    for (int j = n-; j >= ; j--) {

        //最后一个元素和第一个元素进行交换
        int tmp = a[];
        a[] = a[j];
        a[j] = tmp;

        int i = j /  - ;
        CreatHeap(a, i, j);
    }
}
int main() {
    int a[] = { ,,,,,,,,,,,,,,, };
    int n = sizeof(a) / sizeof(int);
    HeapSort(a, n);
    printf("排序好的数组为：");
    for (int l = ; l < n; l++) {
        printf("%d ", a[l]);
    }
    printf("\n");
    return ;
}

分析：

　　最差、最优‘平均时间复杂度都为O(nlogn)，其中堆的每次创建重构花费O(lgn)，需要创建n次。辅助空间O（1）。稳定性：不稳定。

四.归并排序

　　基本思想：归并算法应用到分治策略，简单说就是把一个答问题分解成易于解决的小问题后一个个解决，最后在把小问题的一步步合并成总问题的解。这里的排序应用递归来把数组分解成一个个小数组，直到小数组的数位有序，在把有序的小数组两两合并而成有序的大数组。

　　下图为展示如何归并的合成一个数组。

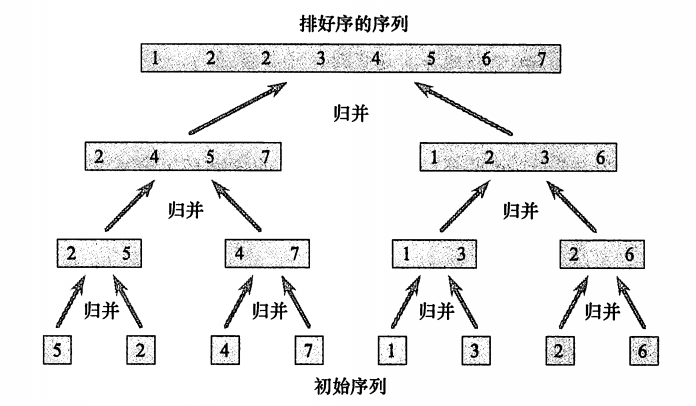
　　下图展示了归并排序过程各阶段的时间花费。

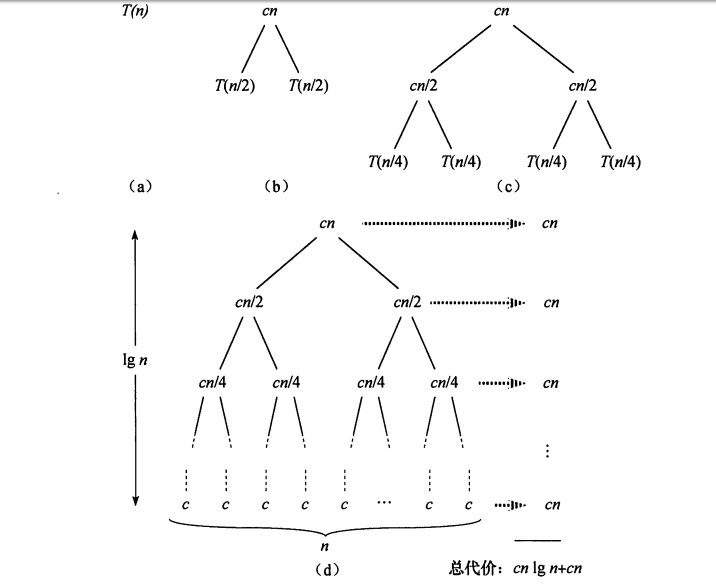
#include <stdio.h>
#include <limits.h>

// 合并两个已排好序的数组
void Merge(int a[], int left, int mid, int right)
{
    int len = right - left + ;        //    数组的长度
    int *temp = new int[len];       // 分配个临时数组
    int k = ;
    int i = left;                   // 前一数组的起始元素
    int j = mid + ;                // 后一数组的起始元素
    while (i <= mid && j <= right)
    {
        //    选择较小的存入临时数组
        temp[k++] = a[i] <= a[j] ? a[i++] : a[j++];
    }
    while (i <= mid)
    {
        temp[k++] = a[i++];
    }
    while (j <= right)
    {
        temp[k++] = a[j++];
    }
    for (int k = ; k < len; k++)
    {
        a[left++] = temp[k];
    }
}

// 递归实现的归并排序
void MergeSort(int a[], int left, int right)
{
    if (left == right)
        return;
    int mid = (left + right) / ;
    MergeSort(a, left, mid);
    MergeSort(a, mid + , right);
    Merge(a, left, mid, right);
}

int main() {
    int a[] = { ,,,,,,,,,, };
    int n = sizeof(a) / sizeof(int);
    MergeSort(a, , n - );
    printf("排序好的数组为：");
    for (int k = ; k < n; ++k)
        printf("%d ", a[k]);
    printf("\n");
    return ;
}

分析：

　　最差、最优、平均时间复杂度都为O(nlogn)，其中递归树共有lgn+1层，每层需要花费O(n)。辅助空间O(n)。稳定性：稳定。