找到最大或最小的N个元素---heapq模块

堆排序heapq的用法

基本用法：

复杂数据结构：

# coding=utf-
# example.py
# Example of using heapq to find the N smallest or largest items
import heapq
portfolio = [
   {'name': 'IBM', 'shares': , 'price': 91.1},
   {'name': 'AAPL', 'shares': , 'price': 543.22},
   {'name': 'FB', 'shares': , 'price': 21.09},
   {'name': 'HPQ', 'shares': , 'price': 31.75},
   {'name': 'YHOO', 'shares': , 'price': 16.35},
   {'name': 'ACME', 'shares': , 'price': 115.65}
]
cheap = heapq.nsmallest(, portfolio, key=lambda s: s['price'])   #对price进行排序
expensive = heapq.nlargest(, portfolio, key=lambda s: s['price'])
print(cheap)
print(expensive)

输出结果：

H:\Python27_64\python.exe H:/myfile/python-cookbook-master/src//finding_the_largest_or_smallest_n_items/example.py
[{'price': 16.35, 'name': 'YHOO', 'shares': }, {'price': 21.09, 'name': 'FB', 'shares': }, {'price': 31.75, 'name': 'HPQ', 'shares': }]
[{'price': 543.22, 'name': 'AAPL', 'shares': }, {'price': 115.65, 'name': 'ACME', 'shares': }, {'price': 91.1, 'name': 'IBM', 'shares': }]

进程已结束,退出代码0

列出一些常见的用法：

heap = []#建立一个常见的堆

heappush(heap,item)#往堆中插入一条新的值

item = heappop(heap)#弹出最小的值

item = heap[0]#查看堆中最小的值，不弹出

heapify(x)#以线性时间将一个列表转为堆

item = heapreplace(heap,item)#弹出一个最小的值，然后将item插入到堆当中。堆的整体的结构不会发生改变。
heappoppush()#弹出最小的值，并且将新的值插入其中

merge()#将多个堆进行合并

nlargest(n , iterbale, key=None)从堆中找出做大的N个数，key的作用和sorted( )方法里面的key类似，用列表元素的某个属性和函数作为关键字

实验：

a=range(,,-)
print a
[, , , , ]
print heapq.nlargest(,a)
[, , ]
heapq.heapify(a)
print a,a[]
[, , , , ]
print heapq.heappop(a),heapq.heappop(a)

print a,'>>>'
[, , ] >>>
heapq.heappush(a,) 　　　　　#直接放在堆的最后
print a
[, , , ]
heapq.heapreplace(a,7.5)    #删一个左边的，item插进去
print a
[, 7.5, , ]
heapq.heappushpop(a,8.5)    #删一个左边的，item插最后
print a
[7.5, , , 8.5]
a.sort()
print a
[7.5, , 8.5, ]
print a[]

#多个堆进行合并

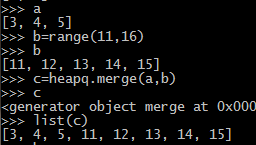
b=range(,)
heapq.heapify(b)
c=range(,)
c.append([,])
print c
[, , , [, ]]

heapq.heapify(c)
print c
[, , , [, ]]

print list(heapq.merge(b,c))    
[, , , , , , [, ]]