【BZOJ 3729】3729: Gty的游戏 （Splay维护dfs序+博弈）

未经博主同意不得转载

3729: Gty的游戏

Time Limit: 20 Sec  Memory Limit: 128 MB
Submit: 448  Solved: 150

Description

某一天gty在与他的妹子玩游戏。
妹子提出一个游戏，给定一棵有根树，每个节点有一些石子，每次可以将不多于L的石子移动到父节点，询问
将某个节点的子树中的石子移动到这个节点先手是否有必胜策略。
gty很快计算出了策略。
但gty的妹子十分机智，她决定修改某个节点的石子或加入某个新节点。
gty不忍心打击妹子，所以他将这个问题交给了你。
另外由于gty十分绅士，所以他将先手让给了妹子。

Input

第一行两个数字，n和L,n<=5*10^4,L<=10^9
第二行n个数字，表示每个节点初始石子数。
接下来n-1行，每行两个整数u和v，表示有一条从u到v的边。
接下来一行一个数m，表示m组操作。
接下来m行，每行第一个数字表示操作类型
若为1，后跟一个数字v，表示询问在v的子树中做游戏先手是否必胜。
若为2，后跟两个数字x，y表示将节点x的石子数修改为y。
若为3，后跟三个数字u,v,x，表示为u节点添加一个儿子v，初始石子数为x。
在任意时刻，节点数不超过5*10^4。

Output

对于每个询问，若先手必胜，输出"MeiZ",否则输出"GTY"。
另，数据进行了强制在线处理，对于m组操作，除了类型名以外，都需要异或之前回答为"MeiZ"的个数。

Sample Input

2 1000
0 0
1 2
1
1 1

Sample Output

GTY

HINT

Source

By wangxz

【分析】

　　膜奥爷爷啦~~

　　好吧，就是首先，阶梯尼姆，很明显吧。就是把距离根节点为奇数层的异或起来就好了。

　　那就是差不多维护子树的异或和，但是树是动态的。【表示动态树我真的很垃圾，splay忘光，LCT不会，前面做的题都是离线的【如果离线就很快就会做了

所以接下来要学学动态树了。。

　　用splay维护dfs序，和之前差不多嘛，一棵树的子树的dfs序记录了st和ed之后，查询区间[st,ed]就行了。

　　splay就是能求出键值在某范围里面的东西【具体维护什么，和啊，最大值啊，都是你决定的】，但实际splay树上维护的是splay树子树上的东西。

　　这时，你只要把st splay到跟，ed splay到根的右儿子，那么ed的做儿子表示的区间就是[st+1,ed-1]你直接问它的子树就好了。

　　实际上，并不需要实际的dfs序，只要你按顺序插入的，那splay树就是有序的，你记录每个点的st和ed，到时找前驱后继就好了。

　　可以选择看图：

　　

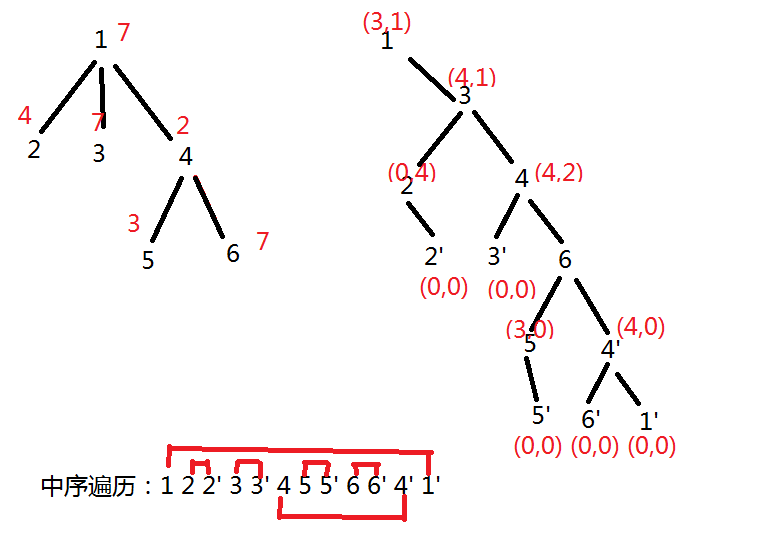
　　左图是原树，右图是splay树。红色是值。splay树的中序遍历就是dfs序，splay树上红色的两个维护的是子树内dep为奇和偶的点的异或和。

　　有意义的点我打在左端点，右端点的值均为0。

　　splay的时候upd一下把左右儿子的值跟自己异或一下就能维护那个异或和了。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<map>
 using namespace std;
 #define Maxn 400010

 int n,Mod;

 int w[Maxn];
 int nl[Maxn],nr[Maxn];
 map<int,int> z;

 struct node
 {
     int x,y,next;
 }t[Maxn*];
 int len,first[Maxn];
 void ins(int x,int y)
 {
     t[++len].x=x;t[len].y=y;
     t[len].next=first[x];first[x]=len;
 }

 struct sp
 {
     int son[],fa,d,a1,a2;
     bool dep;
 }tr[Maxn*];int tot;

 void upd(int x)
 {
     int lc=tr[x].son[],rc=tr[x].son[];
     tr[x].a1=tr[lc].a1^tr[rc].a1;
     tr[x].a2=tr[lc].a2^tr[rc].a2;
     if(!tr[x].dep) tr[x].a2^=tr[x].d;
     else tr[x].a1^=tr[x].d;
 }
 void rot(int x)
 {
     int fa=tr[x].fa,yy=tr[fa].fa;
     int w=tr[fa].son[]==x?:;
     tr[fa].son[-w]=tr[x].son[w];
     if(tr[x].son[w]) tr[tr[x].son[w]].fa=fa;
     if(yy)
     {
         if(tr[yy].son[]==fa) tr[yy].son[]=x;
         else tr[yy].son[]=x;
     }tr[x].fa=yy;
     tr[x].son[w]=fa;tr[fa].fa=x;
     upd(fa);upd(x);
 }
 void splay(int x,int nf)
 {
     while(tr[x].fa!=nf)
     {
         int fa=tr[x].fa,yy=tr[fa].fa;
         if(yy==nf) rot(x);
         else
         {
             if((tr[yy].son[]==fa)==(tr[fa].son[]==x)) {rot(fa);rot(x);}
             else {rot(x);rot(x);}
         }
     }
 }
 int Lower(int x)
 {
     splay(x,);
     x=tr[x].son[];
     while(tr[x].son[]) x=tr[x].son[];
     return x;
 }
 void insert(int fa,int x)
 {
     int r=Lower(fa);
     splay(fa,);splay(r,fa);
     tr[r].son[]=x;
     tr[x].fa=r;
     upd(r);upd(fa);
 }
 void dfs(int x,int fa)
 {
     tr[x].dep=!tr[fa].dep;
     if(fa)
     {
         tr[nl[x]].son[]=nr[x];tr[nr[x]].fa=nl[x];
         tr[nl[x]].d=w[x];upd(nr[x]);upd(nl[x]);
         insert(fa,x);
     }
     for(int i=first[x];i;i=t[i].next) if(t[i].y!=fa)
     {
         int y=t[i].y;
         dfs(y,x);
     }
 }

 int main()
 {
     scanf("%d%d",&n,&Mod);Mod++;
     for(int i=;i<=n;i++) {scanf("%d",&w[i]);z[i]=i;w[i]%=Mod;}
     for(int i=;i<n;i++)
     {
         int x,y;
         scanf("%d%d",&x,&y);
         ins(x,y);ins(y,x);
     }
     for(int i=;i<=n;i++) nl[i]=i,nr[i]=i+n;tot=n*;
     tr[].dep=;tr[].son[]=n+;
     tr[].d=w[];tr[n+].fa=;upd(n+);upd();
     dfs(,);
     int q,nw=;
     scanf("%d",&q);
     while(q--)
     {
         int opt,ans;
         int x,y,k;
         scanf("%d",&opt);
         if(opt==)
         {
             scanf("%d",&x);
             x^=nw;
             x=z[x];
             splay(nl[x],);splay(nr[x],nl[x]);
             if(!tr[x].dep) ans=tr[tr[nr[x]].son[]].a1;
             else ans=tr[tr[nr[x]].son[]].a2;
             if(ans==) printf("GTY\n");
             else {printf("MeiZ\n");nw++;}
         }
         else if(opt==)
         {
             scanf("%d%d",&x,&y);
             x^=nw;y^=nw;
             y%=Mod;
             x=z[x];
             splay(nl[x],);
             if(!tr[nl[x]].dep) tr[nl[x]].a2^=y^tr[nl[x]].d;
             else tr[nl[x]].a1^=y^tr[nl[x]].d;
             tr[nl[x]].d=y;
         }
         else
         {
             scanf("%d%d%d",&x,&y,&k);
             x^=nw;y^=nw;k^=nw;
             k%=Mod;x=z[x];z[y]=y=++n;
             nl[y]=++tot;nr[y]=++tot;
             tr[nl[y]].dep=!tr[nl[x]].dep;
             tr[nl[y]].d=k;tr[nr[y]].d=;
             tr[nr[y]].fa=nl[y];
             tr[nl[y]].fa=nl[x];upd(nl[y]);upd(nr[y]);
             insert(nl[x],nl[y]);
         }
     }
     return ;
 }

【AC了还是很兴奋的。。。以后要多做点dfs序，splay之类的。。

2017-03-30 16:39:42