P1979华容道（神仙题）

题目描述

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

在一个 $ n \times m $ 棋盘上有 $ n \times m $ 个格子，其中有且只有一个格子是空白的，其余 $ n \times m -1 $ 个格子上每个格子上有一个棋子，每个棋子的大小都是 $ 1 \times 1 $ 的；
有些棋子是固定的，有些棋子则是可以移动的；
任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。

游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

给定一个棋盘，游戏可以玩 $ q $ 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次玩的时候，空白的格子在第 $ EX_i $ 行第$ EY_i $ 列，指定的可移动棋子的初始位置为第 $ SX_i $ 第 $ SY_i $ 列，目标位置为第 $ TX_i $ 行第 $ TY_i $ 列。

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

输入输出格式

输入格式：

第一行有 33个整数，每两个整数之间用一个空格隔开，依次表示n,m,qn,m,q；

接下来的 nn 行描述一个n \times mn×m 的棋盘，每行有mm个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，00 表示该格子上的棋子是固定的，11 表示该格子上的棋子可以移动或者该格子是空白的。

接下来的 qq 行，每行包含 66 个整数依次是 EX_i,EY_i,SX_i,SY_i,TX_i,TY_iEXi,EYi,SXi,SYi,TXi,TYi，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

输出格式：

共qq 行，每行包含 11 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出$−1$。

输入输出样例

输入样例#1:

3 4 2

0 1 1 1

0 1 1 0

0 1 0 0

3 2 1 2 2 2

1 2 2 2 3 2

输出样例#1：

2

-1

说明

【输入输出样例说明】

棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

第一次游戏，空白格子的初始位置是 (3,2)(3,2)（图中空白所示），游戏的目标是将初始位置在(1, 2)(1,2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)(2,2)（图中红色的格子）上。

移动过程如下：

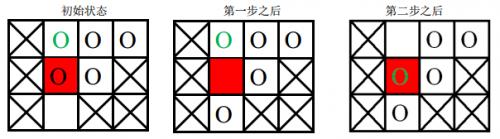
第二次游戏，空白格子的初始位置是(1, 2)(1,2)（图中空白所示），游戏的目标是将初始位置在(2, 2)(2,2)上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)(3,2)上。

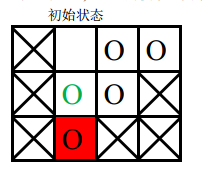
要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置(2,2)(2,2)上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置，游戏无法完成。

【数据范围】

对于$30\%$的数据，$1 ≤ n, m ≤ 10,q = 1$；

对于 $60\%$的数据，$1 ≤ n, m ≤ 30,q ≤ 10$；

对于 $100\%$的数据，$1 ≤ n, m ≤ 30,q ≤ 500$。

炸一看两个点感觉无从下手（其实一开始我也蒙了）：

但其实是起始点要走到终点就必须带着空格子走（因为没有空格子无法移动）