SMU Summer 2024 Contest Round 2

SMU Summer 2024 Contest Round 2

Sierpinski carpet

题意

给一个整数 n ，输出对应的 \(3^n\times 3^n\) 的矩阵。

思路

\(n = 0\) 时是 # ,之后每级矩阵都是中间 \(3^{n-1}\times 3^{n-1}\) 矩阵为全点，周围八个矩阵为上一级的图案，按题意模拟即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    map<int, vector<string>> mp;
    mp[0] = {"#"};

    auto ok = [&](vector<string> s, int m)->vector<string> {
        const int sn = s.size();
        int N = 3;
        for (int i = 1; i < m; i ++) {
            N *= 3;
        }

        vector<string> res(N);
        for (int i = 0; i < N ; i ++) {
            string cs;
            if (i >= N / 3 && i < N / 3 * 2) {
                cs += s[i % sn] + string(sn, '.') + s[i % sn];
            } else {
                cs += s[i % sn] + s[i % sn] + s[i % sn];
            }
            res[i] = cs;
        }

        return res;
    };

    for (int i = 1; i <= n; i ++) {
        mp[i] = ok(mp[i - 1], i);
    }

    for (auto &i : mp[n])
        cout << i << '\n';

    return 0;
}

Consecutive

题意

给一个字符串，\(Q\) 次询问 \([l,r]\) 区间内有多少对相邻且相同的字母。

思路

前缀和处理，注意边界需要特判一下。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, q;
    cin >> n >> q;

    string s;
    cin >> s;

    s = " " + s;
    vector<int> pre(n + 1);
    for (int i = 1; i <= n; i ++) {
        pre[i] = pre[i - 1];
        if (s[i] == s[i + 1]) pre[i] ++;
    }

    while (q--) {
        int l, r;
        cin >> l >> r;
        cout << pre[r] - pre[l - 1] - (r < n && s[r] == s[r + 1]) << '\n';
    }

    return 0;
}

Minimum Width

题意

给你 n 个数，每个数代表一个单词的长度，单词之间挨着的间距为 1 ，行首间距不算，现要求你设计一行的长度 w ，使得这些单词最多排列 m 行，问 w 最小是多少。

思路

w 越大，排列行数一定越小，所以答案满足单调性，可以二分答案，需要注意的是最小边界应该是单词中长度最大的那个，或者在 check 的时候特判一下。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m;
    cin >> n >> m;

    vector<i64> L(n + 2);
    for (int i = 1; i <= n; i ++)
        cin >> L[i];
    L[n + 1] = LLONG_MAX / 2;

    auto check = [&](i64 x) -> bool{
        i64 res = 0, now = 0;
        for (int i = 1; i <= n; i ++) {
            if (x < L[i]) return false;
            now += L[i];
            if (now + 1 + L[i + 1] > x) {
                now = 0;
                res ++;
            } else {
                now ++;
            }
            if (res > m) return false;
        }
        return res <= m;
    };

    i64 l = 0, r = 10000000000000000ll, ans = 1;

    while (l <= r) {
        i64 mid = l + r >> 1;
        if (check(mid)) r = mid - 1, ans = mid;
        else l = mid + 1;
    }

    cout << ans << '\n';

    return 0;
}

Printing Machine

题意

给你 n 个景点的开门时间和持续时间，你想到这些景点去打卡，只要在开门时间或者关门时的那瞬间打卡都可以，但是每打卡一次你需要休息 1 单位时间，问你最多可以打卡多少个景点。

思路

考虑贪心。

要使得打卡景点最多，首先应该考虑开门最早并且持续时间短的景点，所以可以将这些区间先排序，且数据范围给到了 1e18，所以不能去枚举单位时间，对于在当前时间开门的所有景点，我们可以把它的关门时间丢进优先队列里，优先去最早关门的店，如果有景点的关门时间比当前时间更早，说明我们无法去这个景点，弹出队列即可，如果当前时间没有景点开门，我们直接跳到最近一个景点的开门时间即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

using PII = pair<i64, i64>;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;

    vector<PII> td(n);
    for (auto &[t, d] : td) {
        cin >> t >> d;
        d += t;
    }

    sort(td.begin(), td.end());

    priority_queue<i64, vector<i64>, greater<>> Q;
    i64 time = 1, ans = 0, pos = 0;

    while (true) {
        if (Q.empty()) {
            if (pos == n) break;
            time = td[pos].first;
            Q.push(td[pos++].second);
        }
        while (pos < n && td[pos].first == time)
            Q.push(td[pos++].second);
        while (Q.size() && Q.top() < time)
            Q.pop();
        if (Q.size()) ans ++, Q.pop();
        time ++;
    }

    cout << ans << '\n';

    return 0;
}

Nearest Black Vertex

题意

给你 n 个点，m 条边的无向连通图，你可以将这些点染成黑白两色，现给你 k 个条件，要求使得对于第 \(P_i\) 个点，它与离他最近的黑色的点距离为 \(D_i\)，问是否有染色方案可以满足这些条件，有就输出 \(Yes\) 和对应方案，否则输出 \(No\)。

思路

首先可以用 BFS 先计算出每个点到其他点的距离，其次先默认全部点都是黑色，然后去遍历 k 个条件，将与 \(P_i\) 点距离小于 \(D_i\) 的点都染成白色，处理出最终黑色的点，然后再去遍历一次条件，判断所有黑点与 \(P_i\) 的最小距离是否为 \(D_i\) 即可。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, m;
    cin >> n >> m;

    vector g(n + 1, vector<int>());
    for (int i = 0; i < m; i ++) {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }

    vector dis(n + 1, vector<int>(n + 1));
    auto bfs = [&](int s) {
        vector<bool> vis(n + 1);
        queue<array<int, 2>> Q;
        Q.push({s, 0});

        while (Q.size()) {
            auto [u, len] = Q.front();
            Q.pop();

            if (vis[u]) continue;
            vis[u] = 1;

            dis[s][u] = len;
            for (auto &v : g[u]) {
                if (!vis[v] && v != u) {
                    Q.push({v, len + 1});
                }
            }
        }
    };

    for (int i = 1; i <= n; i ++)
        bfs(i);

    int k;
    cin >> k;

    vector<bool> col(n + 1, 1);
    vector<array<int, 2>> pd(k);
    for (auto &[p, d] : pd) {
        cin >> p >> d;
        for (int i = 1; i <= n; i ++)
            if (dis[p][i] < d)
                col[i] = 0;
    }

    for (auto &[p, d] : pd) {
        int t = 1 << 30;
        for (int i = 1; i <= n; i ++)
            if (col[i])
                t = min(t, dis[p][i]);
        if (t != d) {
            cout << "No\n";
            return 0;
        }
    }

    cout << "Yes\n";
    for (int i = 1; i <= n; i ++)
        cout << col[i];

    return 0;
}

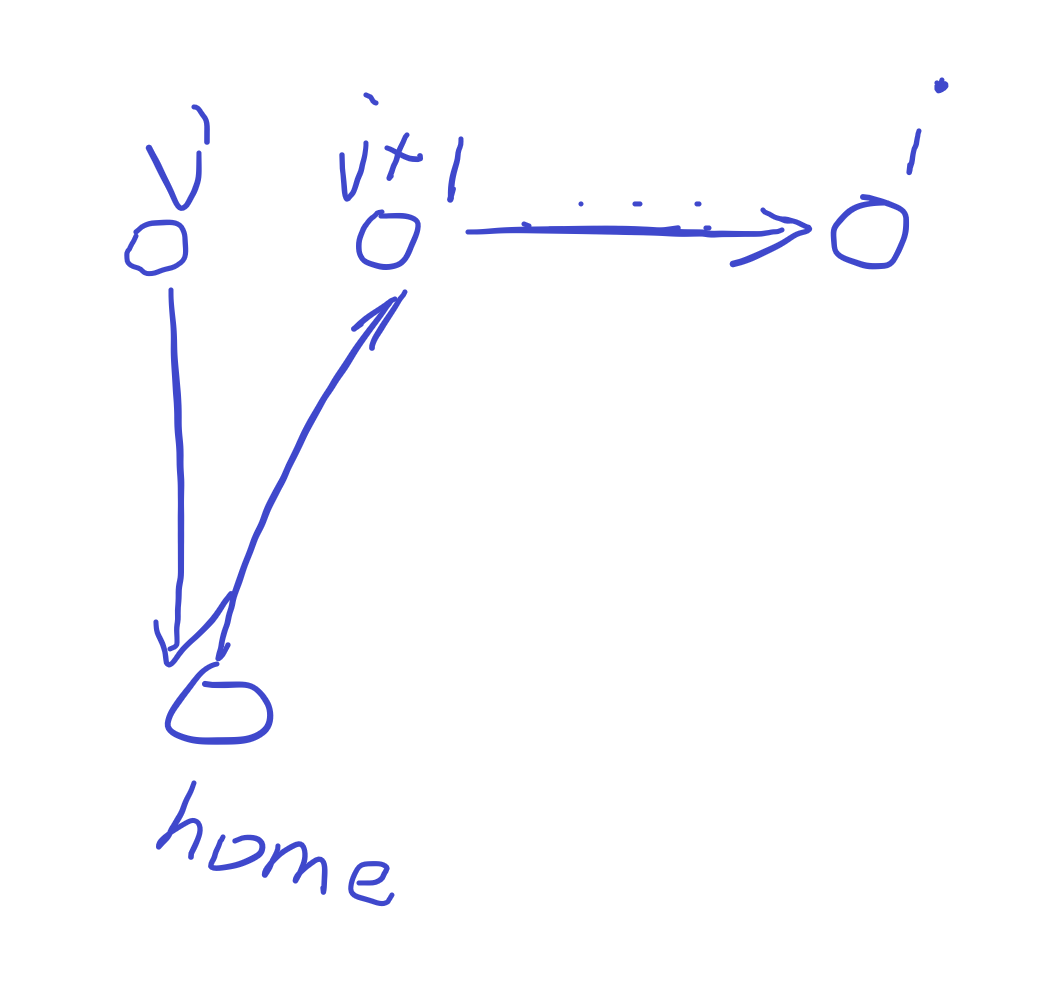
Christmas Present 2

题意

给你一个起点和 n 个孩子的位置，你每次从家出发可以带 k 个礼物，也可以随时回家，现你需要从起点出发按顺序把礼物发个 n 个孩子，送完礼物后最终回到家，问你这个送礼物的最短路程。

思路

因为按顺序发礼物，所以当你处在第 \(i\) 个位置时，就是在 \(i-k\) 到 \(i-1\) 的位置中选择一处回家，考虑dp。

设 \(dp_i\) 为从起点到第 \(i\) 个孩子的最短路程，假设在 \(j\) 处回家，那么转移方程为：

\[dp_i=Min_{i-k}^{i-1}dp_j+home_j+home_{j+1}+dis_{(j+1,i)}
\]

对于 \(dis_{(j+1,i)}\) 可以用前缀和处理成 \(Pre_i - Pre_{j+1}\),那么可化为：

\[dp_i=Min_{i-k}^{i-1}dp_j+home_j+home_{j+1}+Pre_i-Pre_{j+1}\\
=Pre_i+Min_{i-k}^{i-1}dp_j+home_j+home_{j+1}-Pre_{j+1}
\]

对于后面的 \(Min\) 的一串可以使用单调队列 \(O(n)\) 优化。

注意单调队列开始应该放入一个 0，表示给前面的 k 个孩子发礼物后可以不回家。

代码

#include<bits/stdc++.h>

using namespace std;

using i64 = long long;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, k;
    cin >> n >> k;

    vector<array<double, 2>> loc(n + 1);
    for (auto &[x, y] : loc)
        cin >> x >> y;

    vector<double> home(n + 1), pre(n + 1), dp(n + 1);
    for (int i = 1; i <= n; i ++) {
        home[i] = hypot(loc[i][0] - loc[0][0], loc[i][1] - loc[0][1]);
        pre[i] += pre[i - 1];
        pre[i] += hypot(loc[i][0] - loc[i - 1][0], loc[i][1] - loc[i - 1][1]);
    }

    auto calc = [&](int j)->double{
        if (!j) return 0;
        return dp[j] + home[j] + home[j + 1] - pre[j + 1];
    };

    deque<int> Q;
    Q.push_back(0);
    for (int i = 1; i <= n; i ++) {
        dp[i] = pre[i] + calc(Q.front());

        while (Q.size() && Q.front() <= i - k)
            Q.pop_front();

        while (Q.size() && calc(Q.back()) >= calc(i))
            Q.pop_back();

        Q.push_back(i);
    }

    printf("%.15lf", dp[n] + home[n]);

    return 0;
}