Codeforces Round #738 (Div. 2) (A~E)

比赛链接：Here

1559A. Mocha and Math

题意：

给定一个区间，选择区间内的值执行 & 操作使得区间最大值最小化

观察样例发现：令 x = (1 << 30) - 1 后 \(x\&a_0\& a_1\&...a_{n-1} =\) 答案

证明：

我们假设答案是 x。 在它的二进制表示中，只有在所有 \(a_i\) 的二进制表示中该位为 \(1\) 时，该位才会为 \(1\) 。否则，我们可以使用一个操作使 x 中的该位变为 \(0\) ，这是一个较小的答案。

所以我们可以初始设置 \(x=0\) 或者 \(x = 2^n -1\) 。 然后我们对序列进行迭代，使 \(x=x\&a_i\) ，最终 x 是 anwser。

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int n;
    cin >> n;
    int x = (1 << 30) - 1;
    for (int i = 0, a; i < n; ++i) {
        cin >> a;
        x &= a;
    }
    cout << x << "\n";
}

1559B.Mocha and Red and Blue

根据贪心思想，找到第一个非 ? 的下标，然后根据下标位置的值去枚举情况即可

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int _; for (cin >> _; _--;) {
        int n; string s;
        cin >> n >> s;
        for (int i = 0; i < n; ++i)
            if (s[i] == '?' and i and s[i - 1] != '?')
                s[i] = 'R' ^ 'B' ^ s[i - 1];
        if (s.back() == '?') s.back() = 'R';
        for (int i = n - 2; i >= 0; --i)
            if (s[i] == '?') s[i] = 'R' ^ 'B' ^ s[i + 1];
        cout << s << "\n";
    }
}

1559C.Mocha and Hiking

路线规律题，

如果 \(a_1 = 1\) 那么路径肯定有 \([(n + 1)\to 1\to2\to...\to n]\)

如果 \(a_n = 0\) 那么路径为 \([1\to2\to...\to n\to (n + 1)]\)

对于其他情况来说：由于 \(a_1=0∧a_n =1\) ，所以肯定存在整数 \(i\) 使得 \(a_i =0∧a_{i + 1}=1\) ,那么路径为 \([1\to 2\to...\to i\to(n + 1)\to (i + 1)\to (i + 2)\to...\to n]\)

具体证明可以参考哈密顿路径

const int N = 1e4 + 10;
int a[N];
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int _; for (cin >> _; _--;) {
        int n; cin >> n;
        for (int i = 1; i <= n; ++i) cin >> a[i];
        int idx = n;
        for (int i = 1; i < n; ++i)
            if (a[i] == 0 and a[i + 1] == 1) {
                idx = i; break;
            }
        if (a[1] == 1) {
            cout << n + 1 << " ";
            for (int i = 1; i <= n; ++i) cout << i << " \n"[i == n];
            continue;
        }
        for (int i = 1; i <= idx; ++i)
            cout << i << " ";
        cout << n + 1 << " ";
        for (int i = idx + 1; i <= n; ++i) cout << i << " ";
        cout << "\n";
    }
}

1559D1.Mocha and Diana (Easy Version)

D1是一个暴力枚举 + 并查集的裸题，D2就懵逼了，不知道怎么维护

两个森林，同时加边后还是森林，求最多加多少边。

并查集，如果两个森林中，i和j两个节点都不在同一个集合中。加边 i--j

比如上图左边1和5不在一个集合，右边1和5也不在一个集合，加边1-5即可

const int N = 2e3 + 10;
int f1[N], f2[N];
int find1(int x) {return f1[x] == x ? x : f1[x] = find1(f1[x]);}
int find2(int x) {return f2[x] == x ? x : f2[x] = find2(f2[x]);}
void merge1(int x, int y) { f1[find1(x)] = find1(y);}
void merge2(int x, int y) { f2[find2(x)] = find2(y);}
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int n, m1, m2;
    cin >> n >> m1 >> m2;
    for (int i = 1; i <= n; ++i) f1[i] = f2[i] = i;
    for (int i = 1, u, v; i <= m1; ++i) {
        cin >> u >> v;
        merge1(u, v);
    }
    for (int i = 1, u, v; i <= m2; ++i) {
        cin >> u >> v;
        merge2(u, v);
    }
    cout << min(n - m1 - 1, n - m2 - 1) << "\n";
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j) {
            if (j == i) continue;
            if (find1(i) != find1(j) && find2(i) != find2(j)) {
                f1[find1(i)] = find1(j);
                f2[find2(i)] = find2(j);
                cout << i << " " << j << '\n';
            }
        }
}

1559D2. Mocha and Diana (Hard Version)

参考 B站up主 爱打CF的小赵同学

下面，我们称两个森林为左森林和右森林

如下图

左森林1和2连接

右森林1和4连接

首先，对于左森林和右森林中的某个节点j，同时和节点1不在一棵树上，即左森林中1和j不在一棵树上，右森林中1和j不在一棵树上。

那么就在两个森林中将1和j连接。

左森林和右森林中，节点1和节点3都不在一棵树上，连接1 3这条边，如图

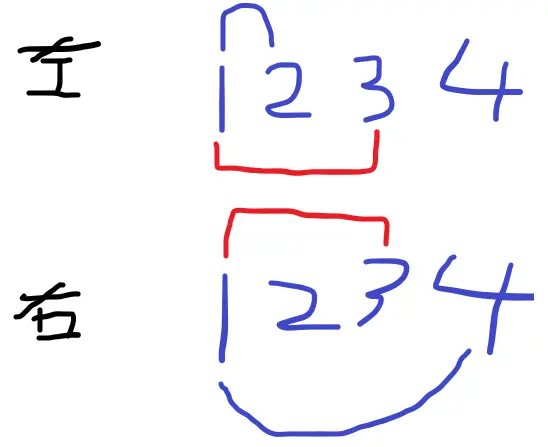
连接之后，还有一类节点可以连接，左森林的i和右森林的j。i和j满足以下条件：

左森林中，1和i在一棵树上，1和j不在一棵树上 ；在右森林中，1和i不在一棵树上，1和j在一棵树上

类似于

节点2在左森林和1相连，节点4在右森林和1相连，则连接2 4 如图

struct DSU {
    vector<int> f, siz;
    DSU(int n) : f(n), siz(n, 1) {iota(f.begin(), f.end(), 0);}
    int find(int x) {return x == f[x] ? x : f[x] = find(f[x]);}
    bool same(int x, int y) {return find(x) == find(y);}
    bool merge(int x, int y) {
        x = find(x), y = find(y);
        if (x == y) return false;
        siz[x] += siz[y];
        f[y] = x;
        return true;
    }
    int size(int x) {return siz[find(x)];}
};
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int n, m1, m2;
    cin >> n >> m1 >> m2;
    DSU f1(n), f2(n);
    for (int i = 0, u, v; i < m1; ++i) {
        cin >> u >> v;
        --u, --v;
        f1.merge(u, v);
    }
    for (int i = 0, u, v; i < m2; ++i) {
        cin >> u >> v;
        --u, --v;
        f2.merge(u, v);
    }
    int ans = n - 1 - max(m1, m2);
    cout << ans << "\n";
    vector<int> v1[n], v2[n];
    while (ans > 0) {
        for (int i = 0; i < n; ++i) v1[i].clear(), v2[i].clear();
        for (int i = 0; i < n; ++i) {
            v1[f1.find(i)].push_back(i);
            v2[f2.find(i)].push_back(i);
        }
        int i = 0, j = 0;
        while (1) {
            while (i < n && f1.find(i) != i) i += 1;
            while (j < n && f2.find(j) != j) j += 1;
            if (i == n || j == n) break;

            int a = -1, b = -1, c = -1, d = 0;
            for (auto x : v1[i]) {
                if (!f2.same(x, j)) a = x;
                else c = x;
            }
            for (auto x : v2[j]) {
                if (!f1.same(x, i)) b = x;
                else c = x;
            }

            if (a != -1 && b != -1) {
                cout << a + 1 << " " << b + 1 << "\n";
                f1.merge(a, b);
                f2.merge(b, a);
            } else {
                while (f1.same(d, i) || f2.same(d, j)) d += 1;
                cout << c + 1 << " " << d + 1 << "\n";
                f1.merge(c, d);
                f2.merge(c, d);
            }
            ans -= 1;
            i += 1, j += 1;
        }
    }
}

1559E. Mocha and Stars

E题在赛时没想到正解，现在学习一下官方的题解

说实话，似乎E题在多校见过？

首先让我们忽略 \(\gcd\) 的限制，令 \(f([l_1,l_2,...,l_n],[r_1,r_2,...,r_n],M)\) 为整数 \((a_1,a_2,..,a_n)\) 的个数满足以下两个条件

• \(\sum\limits_{i=1}^na_i\le m\)
• 对于所有的 i ，\(a_i\) 都在 \([l_i,r_i]\) 范围之间

所以我们可以通过前缀和优化背包DP来达到在 \(\mathcal{O}(nM)\) 内完成计算

此时再来考虑 \(\gcd\) 的约束条件，设 \(μ(n)\) 为莫比乌斯函数，\(g(a_1,a_2,…,a_n)\)为 \(1\) ，如果\((a_1,a_2,⋯,a_n)\) 满足我们提到的两个条件（没有 \(\gcd\) 的约束），否则为 \(0\) 。

我们想要的答案是：

\[\begin{array}{ll}
\sum\limits_{a_1=l_1}^{r_1}\sum\limits_{a_2=l_2}^{r_2}...\sum\limits_{a_n=l_n}^{r_n}[\gcd(a_1,a_2,...,a_n)=1]g(a_1,a_2,...,a_n) \\
= \sum\limits_{a_1=l_1}^{r_1}\sum\limits_{a_2=l_2}^{r_2}...\sum\limits_{a_n=l_n}^{r_n}g(a_1,a_2,...,a_n)\sum\limits_{d|\gcd(a_1,a_2,...,a_n)}μ(d)\\
=\sum\limits_{a_1=l_1}^{r_1}\sum\limits_{a_2=l_2}^{r_2}...\sum\limits_{a_n=l_n}^{r_n}g(a_1,a_2,...,a_n)\sum\limits_{d|a_1,d|a_2,..,d|a_n}μ(d)\\
=\sum\limits_{d=1}^Mμ(d)\sum\limits_{a_1=⌈\frac{l_1}d⌉}^{⌊\frac{r_1}d⌋}...\sum\limits_{a_n=⌈\frac{l_n}d⌉}^{⌊\frac{r_n}d⌋} g(a_1d,a_2d,...,a_nd)
\end{array}
\]

因为 \(\sum\limits_{i = 1}^n a_id\le M\) 可以被改写成 \(\sum_{i=1}^na_i\le ⌊\frac Md⌋\) ,等价于

\[\sum\limits_{d=1}^Mμ(d)f(⌈\frac {l_1}d⌉,...,⌈\frac {l_n}d⌉,⌊\frac {r_1}d⌋,...,⌊\frac {r_n}d⌋,⌊\frac Md⌋)
\]

时间复杂度：\(\mathcal{O}(n\sum\limits_{i=1}^M⌊\frac Mi⌋) = \mathcal{O}(nM\ log\ M)\)

#define maxn 100086
const int p = 998244353;
int n, m;
int l[maxn], r[maxn];
int f[maxn], sum[maxn];
int cal(int d) {
    int M = m / d;
    f[0] = 1;
    for (int i = 1; i <= M; i++) f[i] = 0;
    for (int i = 1; i <= n; i++) {
        int L = (l[i] + d - 1) / d, R = r[i] / d;
        if (L > R) return 0;
        for (int j = 0; j <= M; j++) sum[j] = (f[j] + (j ? sum[j - 1] : 0)) % p;
        for (int j = 0; j <= M; j++) {
            f[j] = ((j - L >= 0 ? sum[j - L] : 0) + p - (j - R - 1 >= 0 ? sum[j - R - 1] : 0)) % p;
        }
    }
    int ans = 0;
    for (int i = 1; i <= M; i++) ans = (ans + f[i]) % p;
    return ans;
}
int prm[maxn], cnt, mu[maxn];
bool tag[maxn];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> l[i] >> r[i];
    mu[1] = 1;
    for (int i = 2; i <= m; i++) {
        if (!tag[i]) prm[++cnt] = i, mu[i] = p - 1;
        for (int j = 1; j <= cnt && prm[j] * i <= m; j++) {
            tag[i * prm[j]] = true;
            if (i % prm[j]) mu[i * prm[j]] = (p - mu[i]) % p;
            else break;
        }
    }
    int ans = 0;
    for (int i = 1; i <= m; i++) ans = (ans + 1ll * mu[i] * cal(i)) % p;
    cout << ans;
}

最后在看H神的代码时发现另外的一个代码思路

const int mod = 998244353;
void add(int &u, int v) {
    u += v;
    if (u >= mod) u -= mod;
}
void sub(int &u, int v) {
    u -= v;
    if (u < 0) u += mod;
}
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int n, m; cin >> n >> m;
    vector<int> l(n), r(n);
    vector<int> np(m + 1), ans(m + 1), p;
    for (int i = 0; i < n; i += 1) cin >> l[i] >> r[i];
    for (int i = 2; i <= m; i += 1) {
        if (not np[i]) {
            p.push_back(i);
            for (int j = i * 2; j <= m; j += i) np[j] = 1;
        }
    }
    for (int i = 1; i <= m; i += 1) {
        vector<int> L(n), R(n);
        int M = m / i, ok = 1;
        for (int j = 0; j < n; j += 1) {
            L[j] = (l[j] + i - 1) / i;
            R[j] = r[j] / i;
            if (L[j] > R[j]) ok = 0;
            M -= L[j];
            R[j] -= L[j];
        }
        if (not ok or M < 0) continue;
        vector<int> dp(M + 1);
        dp[0] = 1;
        for (int j = 0; j < n; j += 1) {
            for (int i = 1; i <= M; i += 1) add(dp[i], dp[i - 1]);
            for (int i = M; i >= 0; i -= 1)
                if (i > R[j]) sub(dp[i], dp[i - R[j] - 1]);
        }
        for (int x : dp) add(ans[i], x);
    }
    for (int x : p)
        for (int i = 1; i * x <= m; i += 1)
            sub(ans[i], ans[i * x]);
    cout << ans[1];
}