【matlab混沌理论】1.5.洛伦兹模型的分析

洛伦兹方程用于生成y变量的图。这是对三种y初始条件敏感依赖的一个例子。

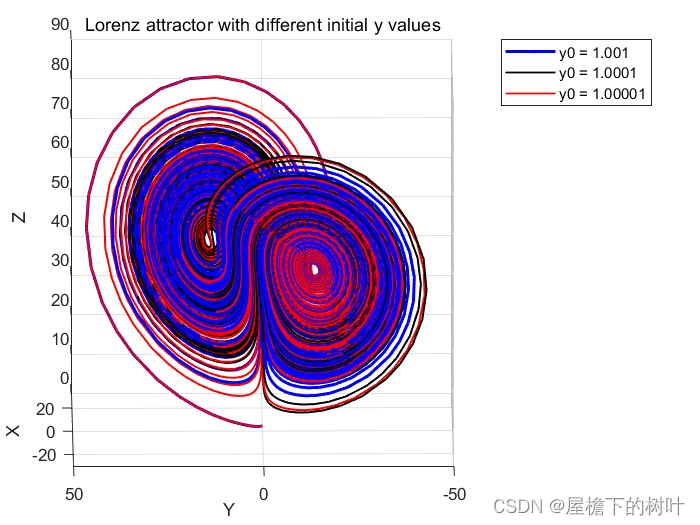
1.洛伦兹吸引子的y敏感依赖的着色图

input:

% 洛伦兹方程用于生成y变量的图。x和z的初始条件保持不变，但y的初始条件在1.001、1.0001和1.00001之间变化

% 定义洛伦兹方程
sigma = 16;
beta = 4;
rho = 45.92;
f = @(t,y) [sigma*(y(2)-y(1)); y(1)*(rho-y(3))-y(2); y(1)*y(2)-beta*y(3)];

% 设置初始条件
y0 = [1.001, 0, 1]; % y 初始值为 1.001
[t1,y1] = ode45(f, [0, 50], y0);

y0 = [1.0001, 0, 1]; % y 初始值为 1.0001
[t2,y2] = ode45(f, [0, 50], y0);

y0 = [1.00001, 0, 1]; % y 初始值为 1.00001
[t3,y3] = ode45(f, [0, 50], y0);

% 绘制图形
plot3(y1(:,1),y1(:,2),y1(:,3),'linewidth',2,'color','b');
hold on
plot3(y2(:,1),y2(:,2),y2(:,3),'linewidth',1,'color','k');
plot3(y3(:,1),y3(:,2),y3(:,3),'linewidth',1,'color','r');
xlabel('X');
ylabel('Y');
zlabel('Z');
title('Lorenz attractor with different initial y values');
legend('y0 = 1.001', 'y0 = 1.0001', 'y0 = 1.00001')
grid on;

output:

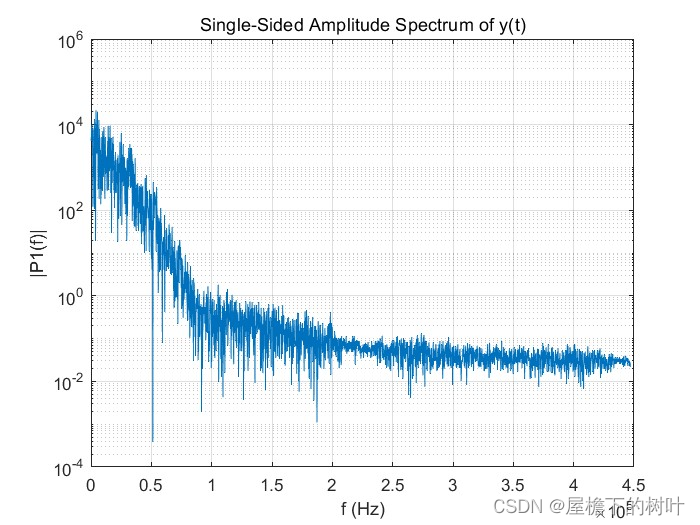
2.洛伦兹模型的y 初始值的频谱变化

input:

% Lorenz，y 初始值情况下的初始条件敏感性
% 绘制一个散点图，显示 y 初始值的频谱从低到高的变化，每个频谱曲线的颜色根据相应的 y 初始值进行着色
% 在另一个子图中显示了 Lorenz 吸引子的演变趋势。

% 定义洛伦兹方程
sigma = 16;
beta = 4;
rho = 45.92;
f = @(t,y) [sigma*(y(2)-y(1)); y(1)*(rho-y(3))-y(2); y(1)*y(2)-beta*y(3)];

% 定义 y 初始条件
y0 = 1.001;

% 计算洛伦兹方程的解
[t, y] = ode45(f, [0, 50], [1, 0, y0]);

% 用 FFT 算法计算洛伦兹方程 y 变量的频谱
N = length(y);
Y = fft(y(:,2));
Pyy = Y.*conj(Y)/N;
f = 1/(t(2)-t(1))*(0:(N/2))/N;

% 绘制频谱图（注意此处使用的是 semilogy 方法）
semilogy(f,Pyy(1:N/2+1))
grid on
title('Single-Sided Amplitude Spectrum of y(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')

% 显示结果

output:

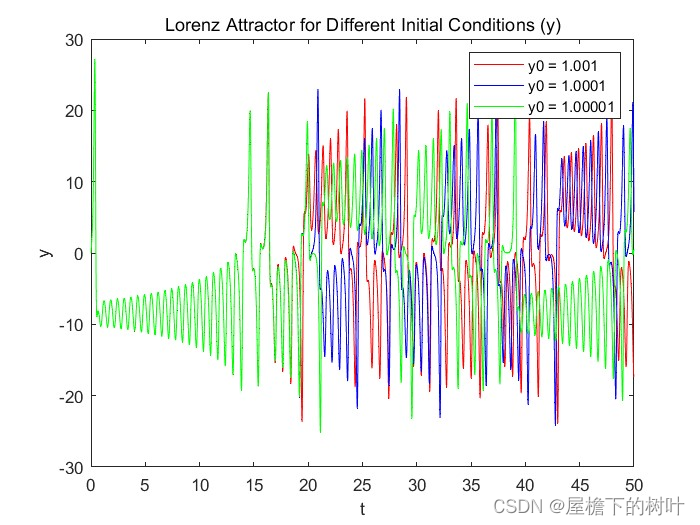
3.不同y初始条件的洛伦兹吸引子轨迹图

input:

% Lorenz 方程在不同的 y 初始条件下生成的轨迹

% 采用数组和循环同时绘制多个初始条件谱图
% 存在上一错误时，可清除所有变量，关闭所有图形窗口
% clear all;
% close all;

% 定义 Lorenz 方程的参数和函数句柄
sigma = 10;
beta = 8/3;
rho = 28;
f = @(t, x) [sigma*(x(2)-x(1)); x(1)*(rho-x(3))-x(2); x(1)*x(2)-beta*x(3)];

% 定义颜色和标记样式
colors = ['r', 'b', 'g'];
markers = ['s', 'o', 'd'];

% 定义 y 初始条件
y0 = [1.001, 1.0001, 1.00001];

% 创建新图形窗口
figure;

% 循环遍历 y 初始值
for i = 1:length(y0)
    % 计算洛伦兹方程的解
    [t, y] = ode45(f, [0, 50], [1, 0, y0(i)]);

    % 绘制 Lorenz 吸引子的 y 轨迹
    plot(t, y(:,2), '-', 'linewidth', 0.5, 'color', colors(i));
    hold on;
end

% 添加图例、坐标轴标签和标题
legend('y0 = 1.001', 'y0 = 1.0001', 'y0 = 1.00001');
xlabel('t');
ylabel('y');
title('Lorenz Attractor for Different Initial Conditions (y)');

ouput:

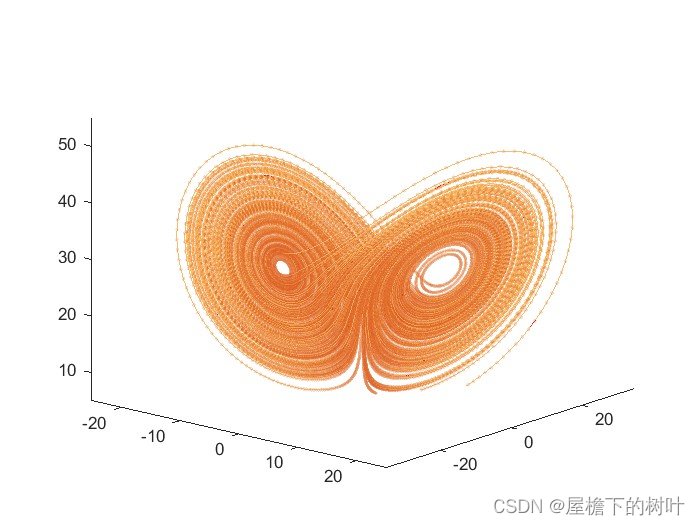
4.吸引子相空间区域内对初始条件的敏感依赖性

input:

% 绘制洛伦兹吸引子（Lorenz attractor）的代码，同时显示出吸引子占据的相空间区域内对初始条件的敏感依赖性

%% 参数设定
sigma = 10;
beta = 8/3;
rho = 28;
dt = 0.005;
max_t = 200;

%% 计算Lorenz attractor
x = 0.1; y = 0.2; z = 0.3;
x_traj = zeros(max_t/dt,1); x_traj(1) = x;
y_traj = zeros(max_t/dt,1); y_traj(1) = y;
z_traj = zeros(max_t/dt,1); z_traj(1) = z;

for i=2:length(x_traj)
    dx_dt = sigma*(y - x);
    dy_dt = x*(rho - z) - y;
    dz_dt = x*y - beta*z;
    x_new = x + dx_dt*dt;
    y_new = y + dy_dt*dt;
    z_new = z + dz_dt*dt;
    x_traj(i) = x_new;
    y_traj(i) = y_new;
    z_traj(i) = z_new;
    x = x_new; y = y_new; z = z_new;
end

%% 绘制Lorenz attractor
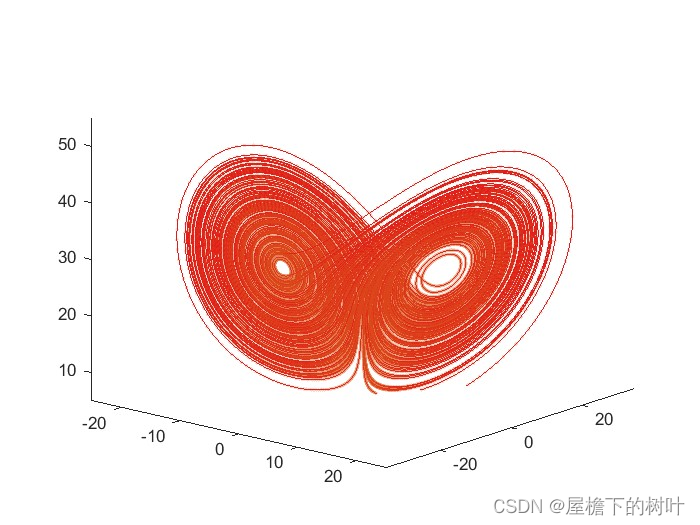
figure('color','black');

plot3(x_traj,y_traj,z_traj, 'color', [0.894,0.102,0.110]); hold on;
scatter3(x_traj,y_traj,z_traj,5,'filled', 'MarkerFaceAlpha',0.2,'MarkerEdgeAlpha',0.2);

title('Lorenz attractor', 'color','white');
xlabel('x', 'color','white'); ylabel('y', 'color','white'); zlabel('z', 'color','white');
axis tight;
view([40,20]); xlim([-25,25]); ylim([-35,35]); zlim([5,55]);

%% 绘制敏感依赖性图
figure('color','black');

delta = 1e-8;
x_traj_perturbed = x_traj+delta*randn(length(x_traj),1);
y_traj_perturbed = y_traj+delta*randn(length(y_traj),1);
z_traj_perturbed = z_traj+delta*randn(length(z_traj),1);

plot3(x_traj,y_traj,z_traj, 'color', [0.894,0.102,0.110]); hold on;
scatter3(x_traj,y_traj,z_traj,5,'filled', 'MarkerFaceAlpha',0.2,'MarkerEdgeAlpha',0.2);
plot3(x_traj_perturbed,y_traj_perturbed,z_traj_perturbed, 'color', [0.980,0.745,0.412]);

title('Sensitive Dependence on Initial Conditions', 'color','white');
xlabel('x', 'color','white'); ylabel('y', 'color','white'); zlabel('z', 'color','white');
axis tight;
view([40,20]); xlim([-25,25]); ylim([-35,35]); zlim([5,55]);

output: